4. Основные методы интегрирования

1) метод непосредственного интегрирования.

Этот метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам и называется методом непосредственного интегрирования.

Примеры:

1. .

2. .

3. .

2) метод интегрирования подстановкой (замена переменной).

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (т.е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно сделать подстановку приобретается практикой и зачастую делается по интуиции.

Пусть требуется вычислить . Сделаем подстановку, где- функция, имеющая непрерывную производную. Тогдаи на основании инвариантности формулы интегрирования неопределенного интеграла получим формулу интегрирования подстановкой′(t)dt. Эта формула называется формулой замены переменных в неопределенном интеграле. После нахождения интеграла правой части этого равенства следует перейти от новой переменнойtинтегрирования назад к старой переменнойx. Иногда целесообразно подбирать подстановку в видетогда, где. Другими словами, первую формулу можно применить справа налево

Примеры: 1). Получим, тогдаи

2) . Пустьи. Подставляя, получим3). Пусть, тогда,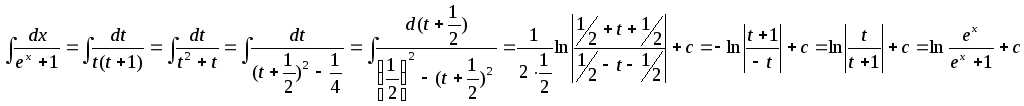3) Метод интегрирования по частям.

Пусть и– функции, имеющие непрерывные производные, тогда. Интегрируя это равенство, получимили.Полученное соотношение получило название формулы интегрирования по частям. Она дает возможность свести вычисления интегралак вычислению интеграла, который может оказаться существенно более простым, чем исходный. Интегрирование по частям состоит в том, что подинтегральное выражение заданного интеграла представляется каким либо образом в виде произведения двух сомножителей u и dv, затем после нахождения v и du используется формула интегрирования по частям. Иногда эту формулу приходится использовать несколько раз. Укажем некоторые виды интегралов, которые удобно вычислять методом интегрирования по частям.

а) интегралы вида ,,, где Р- многочлен,k– число. Удобно положить, а заdvобозначить все остальное.

б) интегралы вида ,,,,, надо положить, аu– все остальное.

в) интегралы вида ,, гдеaиb– числа. Заu можно принять функцию.

Примеры: 1) . Пусть; ; ; (полагая, что с=0). Применяя формулу интегрирования по частям получим

2) . Пусть;получим при

3) .;, следовательно. Для вычисления последнего интеграла снова применили метод интегрирования по частям

Значит . Окончательно

5. Интегрирование рациональных функций.

1) Многочлен. Понятие о рациональных функциях

Функция вида -, как говорилось ранее, называется многочленом (или целой рациональной функцией). Всякий многочлен должен иметь по крайней мере один корень, действительный или мнимый(корнем многочлена называется такое значение х₀переменной х, при котором многочлен). Очевидно, что всякий многочленможно представить в виде, где х₁, х₂, … х_n– корни многочлена, – коэффициент при хⁿ. Множители (х-х₁) в записанном соотношении называются линейными множителями.

Пример: Разложить многочлен на множители. Корни этого многочлена х₁=-1, х₂=1, х₃=2, следовательно.

Можно доказать, что многочлен с действительными коэффициентами разлагается на линейные и квадратные множители с действительными коэффициентами, т.е. многочлен можно предоставить в виде:

……

при этом …, все квадратные трехчлены не имеют вещественных корней.

Пример: .

2) Дробно-рациональная функция

Дробно-рациональной функцией называется функция равная отношению двух многочленов, т.е. , где- многочлен степениm, а- многочлен степениn. Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя, т.е.m<n. В противном случае, еслиm>n, то дробь называется неправильной. Всякую неправильную рациональную дробь- путем деления числителя на знаменатель можно представить в виде суммы многочленаи правильной рациональной дроби, т.е.=+.

Например:

=;

Результат получен при делении столбиком на, где 15 – остаток деления.

Всякую правильную рациональную дробь можно представить (и причем единственным образом) в виде следующей суммы простейших дробей:

, где- некоторые действительные коэффициенты.

Примеры:

1. ;

2. .

Для нахождения неопределенных коэффициентов используют метод сравнения коэффициентов. Суть метода следующая. Правую часть разложения дробиприводим к общему знаменателю. В результате получим тождество=, гдеS(x) – многочлен с неопределенными коэффициентами. Т.к. знаменатели равны, то тождественны и числители, т.е.P(x)=S(x).

Приравнивая коэффициенты при одинаковых степенях x, получим систему уравнения, решая которую и определим коэффициенты.

Пример:

- представить дробь в виде суммы простейших дробей. Согласно сказанному раннее, получим, т.е.

;

отсюда , т.е..

Получим: ;

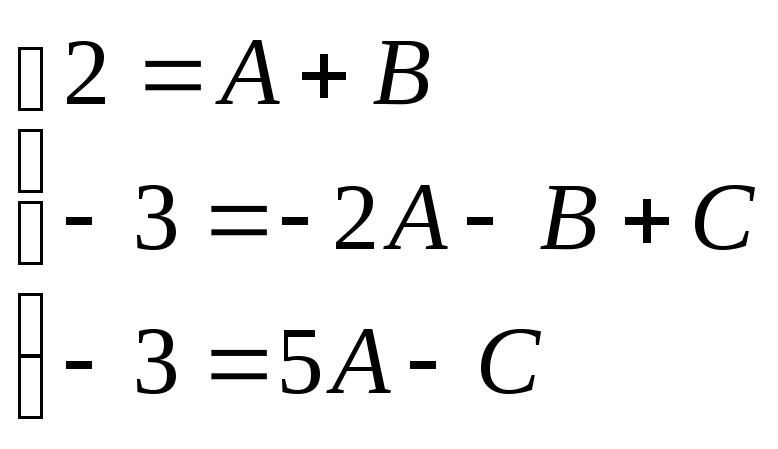Решая найдем, что, ,В=3,.

Следовательно, .

3) интегрирование простейших рациональных дробей

Найдем интегралы от простейших рациональных дробей:

а) (1)

б) (2)

в) вычисление интеграла вида

.

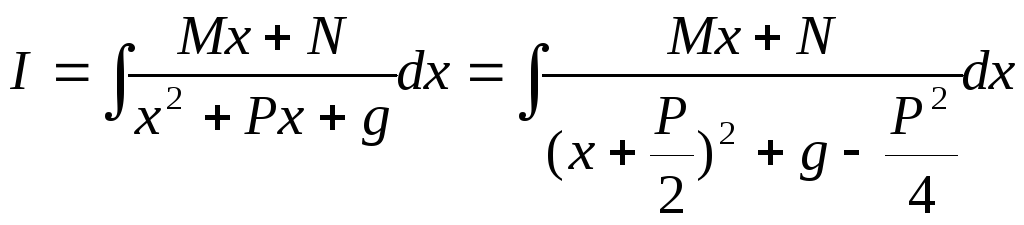, тогдаи. Сделаем подстановку, положим,. Следовательно, после подстановки получим:

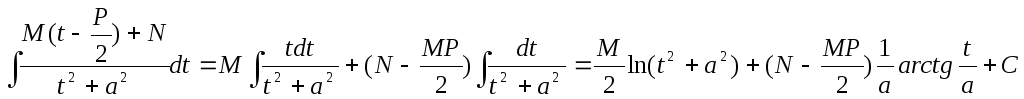и возвращаясь кx, получим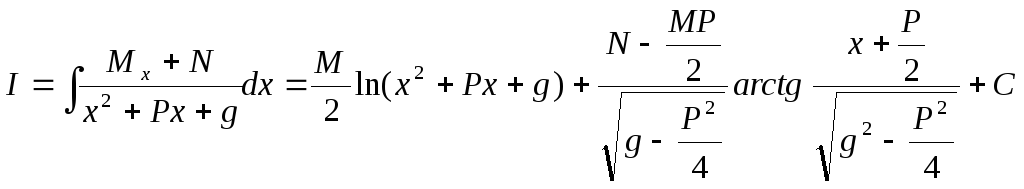

г) Вычисление интеграла вида , где,, данный интеграл подстановкойсводится к сумме двух интеграловПервый интеграл легко вычисляется:. Вычислим второй интеграл:

К последнему применим интегрирование по частям. Положим u=t,, ; тогдаI_k-1. Подставляя это значение в выражения дляI_k, найдем:. Полученное соотношение дает возможность найтиI_kдля любого натурального числа х>1.

д) интегрирование рациональных дробей

Рассмотренный выше материал позволяет сформулировать основные правила интегрирования рациональных дробей.

1. если дробь неправильна, то представить ее в виде суммы многочлена и правильной дроби.

2. Разложив знаменатель правильной рациональной дроби на множители, представить ее в виде суммы простейших рациональных дробей.

3. Проинтегрировать многочлен и полученную сумму простейших дробей.

Пример:

(проделав операции пунктов 1) и 2), получим)

=.

Последний интеграл берем методом подстановки x+1=t, тогдаx=t-1 иdx=dt. Таким образом,. Следовательно,

.