8.4. Решение ду второго порядка с постоянными коэффициентами.

1.Решение лоду второго порядка с постоянными коэффициентами.

Частным случаем рассмотренных выше линейных однородных дифференциальных уравнений является ЛОДУ с постоянными коэффициентами. Пусть одно ЛОДУ второго порядка.

(14)

Где pиg–constвеличины.

Для нахождения общего решения этого уравнения достаточно найти два его частных решения, образующих фундаментальную систему (Теорема 4).

Будем искать частные решения этого уравнения в виде гдеk– некоторое число. Дифференцируя эту функцию два раза и подставляя выражения дляив наше уравнение получим

т.е.или

.

Это уравнение называется характеристическим уравнением ДУ (14).Для его составления достаточно заменить в уравнении (14) соответственно наи 1.

При решении характеристического уравнения возможны следующие три случая:

1. корни иуравнения действительны и различны.

В этом случае частными решениями уравнения (14) является функция .

Они образуют фундаментальную систему решений (линейно независимы) ,следовательно общее решение уравнения (14)в соответствии с формулой (12) имеет вид :

(15)

Пример: Решить уравнение

Составим характеристическое уравнение , решая его получим.Запишем общее решение данного уравнения, где- произвольныеconst.

2. корни ихарактеристического уравнения действительные и равные

.В этом случае имеем лишь одно частное решение

.Кроме того можно показать ,что наряду срешением (14) будет и.

Действительно, подставив в (14) получим :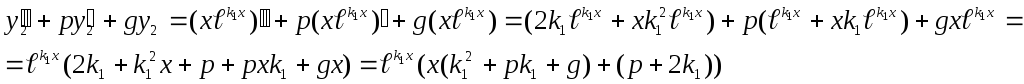

Но т.к.- корень этого характеристического уравнения ,

т.к. по условию.

Поэтому т.е.является решением уравнения (14).Частные решенияиобразуют фундаментальную систему решений ,следовательно в этом случае общее решение ЛОДУ (14) имеет вид

(16)

3. корни икомплексныеВ этом случае частными решениями уравнения (14)являютсяи.По формуле Эйлератогда имеем

(14)

Найдем два действительно частных решения уравнения, для этого составим две линейных комбинации решений и.

и

Функции иявляются решениями уравнения (14),что следует из свойств решений ЛОДУ второго порядка (Теорема 3).Эти решения образуют фундаментальную систему решений, так как они являются линейно независимыми. Поэтомуобщее решение уравнения (14) запишется в виде

(17)

Пример:

Запишем характеристическое уравнение , здесь, тогда общее решение уравнения примет вид

Таким образом, нахождение общего решения ЛОДУ второго порядка с постоянными коэффициентами (14) сводится к нахождению корней характеристического уравнения и выше полученных формул для общих решений (15),(16),(17) уравнений, не прибегая к вычислению интегралов.

Лекция 13

2. Решение лоду n –го порядка с постоянными коэффициентами.

Задача нахождения общего решения ЛОДУ n-го порядкас постоянными коэффициентами

(18)

Где - числа ,решается аналогично случаю уравнения второго порядка с постоянными коэффициентами.

Покажем как это делается.

Частные решения уравнения (18) будем также искать в виде ,гдеk–const.Характеристическим для этого уравнения является алгебраическое уравнениеn-го порядка(19)

Последнее уравнение имеет, как известно, nкорней (в их числе могут быть и комплексные).Обозначим их через.Кстати, не все из корней уравнения (19) обязаны быть различными так, например, уравнениеимеет два одинаковых корняk=2.В этом случае говорят, что корень одинk=2 и имееткратность mk=2 .

Если mk=1 ,то такой корень называютпростым.

Вариант 1. Если все корни уравнения (19) действительны и просты, то функции

являются частными решениями уравнения (18) и образуют фундаментальную систему решений (линейно независимых). Поэтому общее решение уравнения (18) запишется в виде

Пример: Решить

Характеристическое уравнение примет вид и имеет корни.Следовательно- общее решение нашего уравнения.

Вариант 2. Все корни характеристического уравнения действительные, но не все простые (есть корни имеющие кратность) Тогда каждому простому корнюkсоответствует одно частное решение вида,а каждому корнюkкратностисоответствуетmчастных решений.

Пример:

Характеристическое уравнение имеет корни, следовательно

- общее решение.

Вариант 3. Среди корней уравнения (19) есть комплексные корни. Тогда каждой парепростых комплексно сопряженных корней соответствует два частных решения

и,а каждой парекорней кратностисоответствуют 2mчастных решений вида

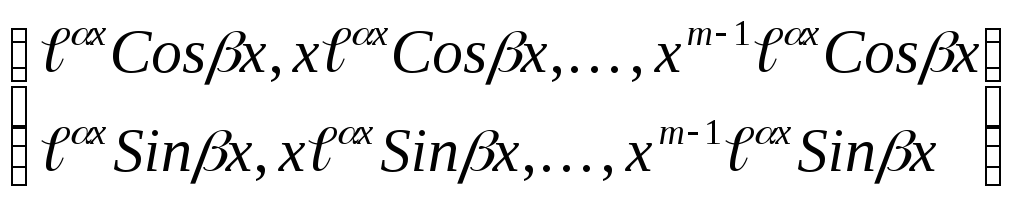
Эти решения, как можно доказать, образуют фундаментальную систему решений.

Пример:

Характеристическое уравнение имеет корни, следовательно

- общее решение уравнения.