5.4. Признак Даламбера

В отличие от признаков сравнения, где все зависит от догадки и записи известных сходящихся и расходящихся рядов признак Даламбера позволяет решить вопрос о сходимости ряда, проделав лишь некоторые операции над самим рядом.

Теорема. Пусть дан ряд с положительными членами и существует конечный или бесконечный предел , тогда ряд сходится прии расходится при.

Доказательство:

Так как , то по определению предела для любогонайдется натуральное числотакое, что привыполняется неравенствоили(2).

Пусть. Можно подобратьтак, что число. Обозначим. Тогда из правой части неравенства (2) получаемили. В силу свойств всех 3 числовых рядов можно считать, чтодля всех. Давая номеруэти значения получим целый набор неравенств:

………..

Т.е. члены ряда меньше соответствующих членов ряда, который сходится как геометрическая прогрессия со знаменателем. Но тогда на основании признака сходимости сходится и ряд. Следовательно, сходится и исходный ряд.

Пусть . В этом случае. Отсюда следует, что, начиная с некоторого номера, выполняется неравенствоили, т.е. члены ряда с увеличением номеравозрастают, поэтому. На основании следствия из необходимого признака этот ряд расходится.

1. Если 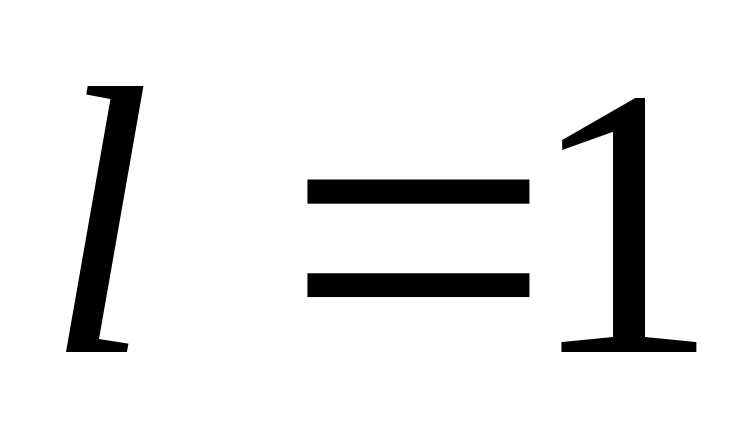, то ряд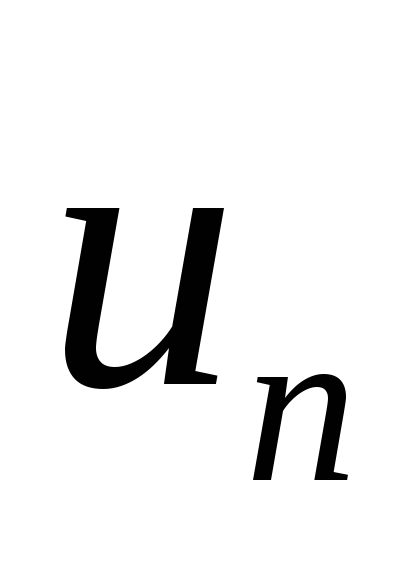может быть как сходящимся, так и расходящимся.

2. Признак Даламбера целесообразно применять, когда общий член ряда содержит выражения вида .

Пример.

Исследовать на сходимость ряд. Находим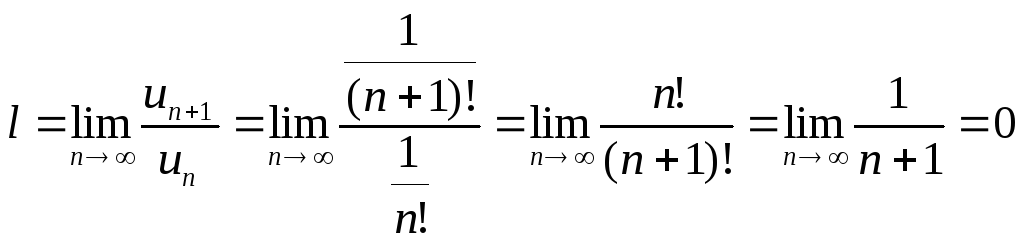. Так как, то данный ряд по признаку Даламбера сходится.

5.5. Радикальный признак Коши

Иногда удобно пользоваться радикальным признаком Коши для исследования сходимости знакоположительного ряда. Этот признак во многом схож с признаком Даламбера.

Теорема. Пусть дан ряд с положительными членами и существует конечный или бесконечный предел. Тогда ряд сходится прии расходится при.

При вопрос о сходимости остается открытым. (Без доказательства).

Пример. Исследовать на сходимость ряд . Так как, то применим признак Коши к ряду. Вычисляем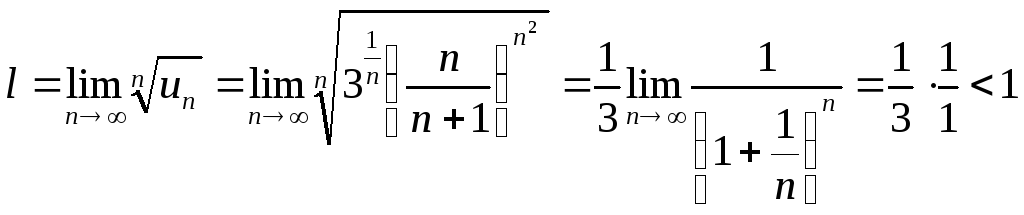, т.е. этот ряд сходится, значит, сходится и исходный ряд согласно свойству 1 числовых рядов.

5.6. Интегральный признак Коши. Обобщенный гармонический ряд

Теорема. Если члены знакоположительного ряда могут быть представлены как числовые значения некоторой непрерывно монотонно убывающей на промежуткефункциитак, чтото

1. еслисходится, то сходится и ряд.

2. если 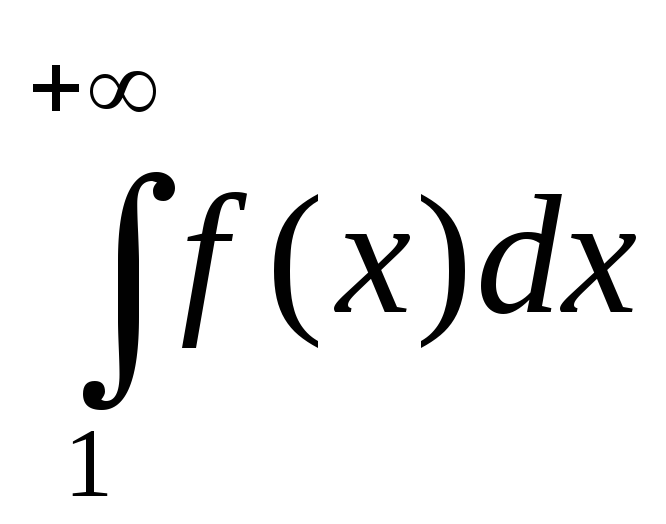расходится, то расходится также и ряд.

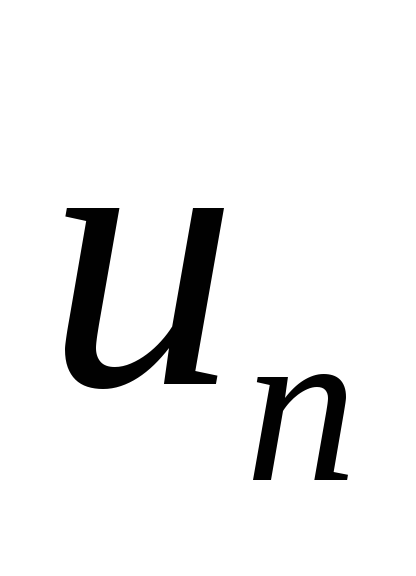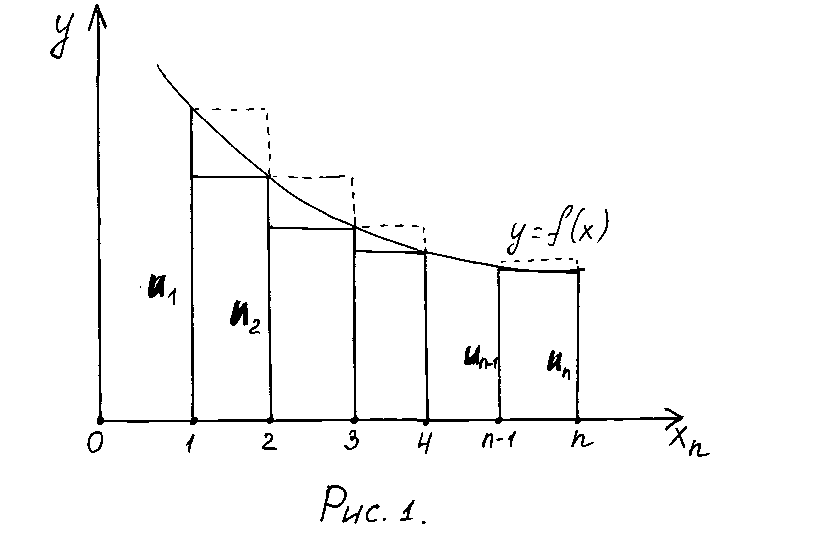
Рассмотрим криволинейную трапецию, ограниченную сверху графиком функции , основанием которой служит отрезок осиотдо(рис.1). Построим входящие и выходящие прямоугольники, основаниями которых служат отрезки. Учитывая геометрический смысл определенного интеграла можно записатьилиили (1).

Случай 1. несобственный интеграл сходится, т.е.. Поскольку<, то с учетом неравенства (1) имеем , т.е..Так как последовательность частичных сумм монотонно возрастает и ограничена сверху (числом ), то по признаку существования предела, имеет предел. Следовательно, рядсходится.

Случай 2. Несобственный интеграл расходится, тогдаи интегралнеограниченно возрастает при. Учитывая, что(см. 1) получаем, чтопри. Следовательно, рядрасходится.

Пример. Исследовать на сходимость ряд . Воспользуемся интегральным признаком Коши. Функцияудовлетворяет условиям теоремы. Поэтому находим. Значит, ряд с общим членомрасходится. Ряд, где– действительное число называетсяобобщенным гармоническим рядом. Для исследования этого ряда на сходимость применим интегральный признак Коши. Рассмотрим функцию . Эта функция непрерывна, монотонно убывает на промежуткеи. Приимеем: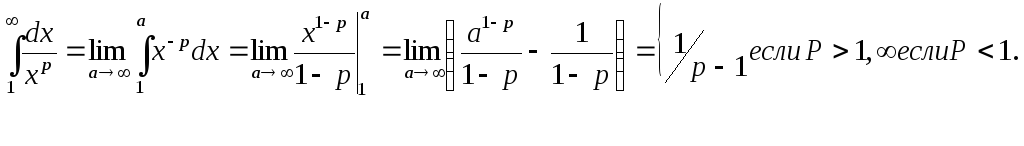. Приимеем гармонический ряд, который расходится (второй способ). Итак, гармонический ряд сходится при, расходится при.

Рассмотренные признаки сходимости знакоположительных рядов позволяют судить о сходимости практически любого положительного ряда.