
- •Лекция 1 Функции нескольких переменных
- •Функция двух переменных
- •Предел функции
- •Непрерывность функции двух переменных
- •Производные и дифференциалы функции нескольких переменных
- •Частные производные высших порядков
- •Дифференцируемость и полный дифференциал функции
- •Дифференциалы высших порядков
- •Производная сложной функции. Полная производная
- •8.Инвариантность формы полного дифференциала
- •Дифференцирование неявной функции
- •Производная по направлению
- •Градиент
- •Экстремум функции двух переменных
- •Необходимые и достаточные условия экстремума
- •Лекции №№2,3
- •II. Неопределенный интеграл
- •2. Свойства неопределенного интеграла
- •3. Таблица основных неопределенных интегралов
- •4. Основные методы интегрирования
- •5. Интегрирование рациональных функций.
- •6. Интегрирование тригонометрических функций
- •7. Интегрирование иррациональных функций
- •Лекция 4
- •III. Определенный интеграл
- •Определение определенного интеграла
- •Геометрический смысл определенного интеграла
- •3) Работа переменной силы
- •Формулы Ньютона-Лейбница
- •Основные свойства определенного интеграла
- •Вычисление определенного интеграла
- •Несобственные интегралы
- •Лекция 5
- •7. Применение определенных интегралов для расчета геометрических и физических величин различного рода
- •7.1. Вычисление площадей плоских фигур
- •7.2 Вычисление длины дуги плоской кривой
- •7.3 Вычисление объема тела
- •8. Приближенное вычисление определенного интеграла
- •8.1. Формулы прямоугольников
- •8.2. Формула трапеций
- •8.3. Формула парабол (Симпсона)
- •Лекция 6,7
- •4. Кратные интегралы
- •4.1. Двойной интеграл. Основные понятия
- •4.2. Геометрический смысл двойного интеграла
- •4.3. Основные свойства двойного интеграла
- •4.4.Вычисление двойного интеграла
- •4.5. Приложения двойного интеграла
- •4.6. Тройной интеграл. Основные понятия
- •4.7. Вычисление тройного интеграла.
- •4.8. Приложения тройного интеграла
- •Лекция 8
- •V. Числовые ряды
- •5.1. Основные понятия
- •5.2. Необходимый признак сходимости числового ряда
- •5.3. Достаточные признаки сходимости знакопостоянных рядов
- •5.4. Признак Даламбера
- •5.5. Радикальный признак Коши
- •5.6. Интегральный признак Коши. Обобщенный гармонический ряд
- •5.7. Знакочередующиеся и знакопеременные ряды Признак Лейбница
- •Общий достаточный признак сходимости знакопеременных рядов
- •5.8. Абсолютная и условная сходимость числовых рядов
- •Лекция №9 Степенные ряды
- •1 Функциональные ряды
- •1.1 Основные понятия
- •2. Некоторые приложения степенных рядов
- •2.1. Приближенное вычисление значений функций
- •2.2. Приближенное вычисление определенных интегралов
- •Лекция №10
- •VII Ряды Фурье
- •7.1. Основные понятия
- •7.2. Тригонометрический ряд Фурье
- •7.3 Разложение в ряд Фурье 2π-периодических функций. Теорема Дирихле
- •7.4. Разложение в ряд Фурье четных и нечетных функций
- •7.5. Разложение в ряд Фурье функций произвольного периода
- •Лекция 11.
- •VIII. Дифференциальные уравнения (д.У.)
- •8.1. Общие сведения на основании понятия о д.У.
- •8.2. Дифференциальное уравнение первого порядка
- •2. Метод Лагранжа
- •Лекция 12
- •8.3.Дифференциальные уравнения высших порядков
- •1.Решение путем понижения порядка уравнения.
- •2.Линейные дифференциальные уравнения высших порядков.
- •8.4. Решение ду второго порядка с постоянными коэффициентами.
- •1.Решение лоду второго порядка с постоянными коэффициентами.
- •Лекция 13
- •2. Решение лоду n –го порядка с постоянными коэффициентами.
- •Линейные неоднородные дифференциальные уравнения (лнду)
- •1.Структура общего решения лнду второго порядка.
- •2.Метод вариации произвольных постоянных.
- •3.Решение лнду второго порядка с постоянными коэффициентами и правой частью специального вида.
- •4.Решение лнду n- го порядка с постоянными коэффициентами и правой специальной частью.
- •Лекция 14
- •2.Системы линейных ду с постоянными коэффициентами.
4.3. Основные свойства двойного интеграла
Свойства двойных интегралов аналогичны свойствам интеграла от функции одной переменной. Поэтому мы просто ограничимся перечислением этих свойств.
1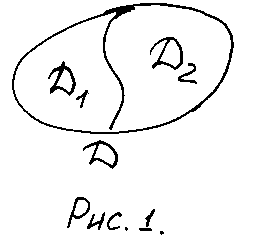 )
)![]() ,
с-const
,
с-const
2)
![]()
3) Если область
![]() разбить линией на две областиD1иD2 такие, что
разбить линией на две областиD1иD2 такие, что
![]() ,а пересечениеD1иD2 состоит лишь из
линии их разделяющей (рис.1), то
,а пересечениеD1иD2 состоит лишь из
линии их разделяющей (рис.1), то
![]() .
.
4) Если в области
![]() имеет место неравенство
имеет место неравенство![]() ≥0
то и
≥0
то и![]() .
Если в области
.
Если в области![]() функция
функция![]() и
и![]() удовлетворяют неравенству
удовлетворяют неравенству![]() ≥
≥![]() ,
то и
,
то и![]() .
.
5)
![]() ,
так как
,
так как![]() .
.
6) Если функция
![]() непрерывна в замкнутой области
непрерывна в замкнутой области![]() ,
площадь которойS, то в
этой области существует такая точка
,
площадь которойS, то в
этой области существует такая точка![]() ,
что
,
что![]() .
Величину
.
Величину![]() называют средним значением функции
называют средним значением функции![]() в области
в области![]() .
.
4.4.Вычисление двойного интеграла
Покажем, что вычисление двойного
интеграла сводится к последовательному
вычислению двух определенных интегралов.
Пусть требуется вычислить двойной
интеграл
![]() ,
где
,
где![]() непрерывна в
непрерывна в![]() .
Тогда, как это было показано выше, двойной
интеграл выражает объем цилиндрического
тела, ограниченного сверху поверхностью
.
Тогда, как это было показано выше, двойной
интеграл выражает объем цилиндрического
тела, ограниченного сверху поверхностью![]() .
Найдем этот объем используя метод
параллельных сечений. Ранее мы показали,
что
.
Найдем этот объем используя метод
параллельных сечений. Ранее мы показали,
что![]() ,
где
,
где![]() - площадь сечения плоскостью,
перпендикулярной о
- площадь сечения плоскостью,
перпендикулярной о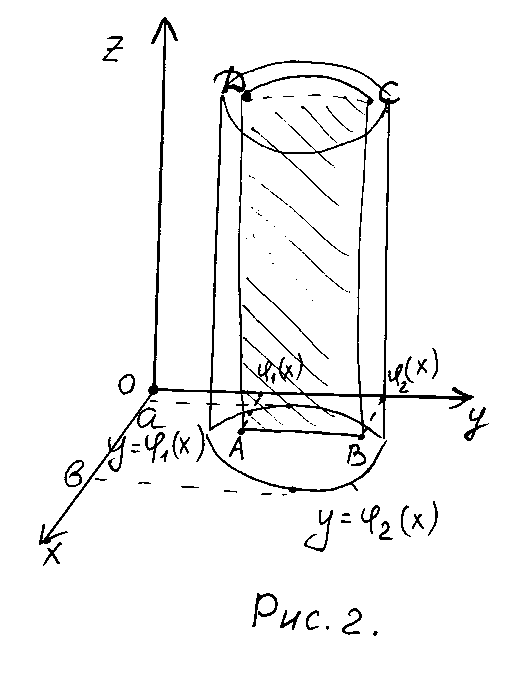 си
ох, а
си
ох, а![]() ,
,![]() - уравнения плоскостей, ограничивающих
данное тело. Положим сначала, что область
- уравнения плоскостей, ограничивающих
данное тело. Положим сначала, что область![]() представляет собой криволинейную
трапецию, ограниченную прямыми
представляет собой криволинейную
трапецию, ограниченную прямыми![]() и
и![]() и кривыми
и кривыми![]() и
и![]() ,
причем функции
,
причем функции![]() и
и![]() непрерывны и таковы, что
непрерывны и таковы, что![]() ≤
≤![]() для всех х. Такая область называется
правильной в
для всех х. Такая область называется
правильной в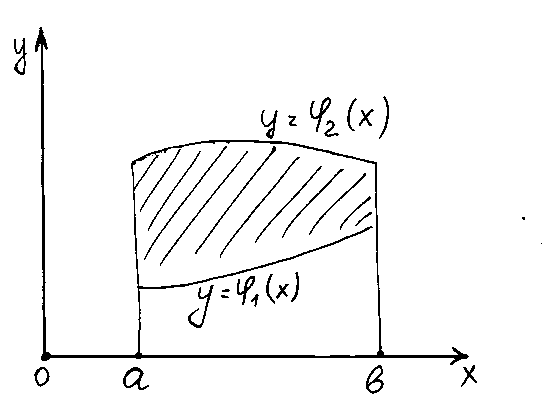 направлении оси оу. Любая прямая,
параллельная оси оу, пересекает границу
области не более, чем в двух точках.
Построим сечение цилиндрического тела
плоскостью, перпендикулярной оси ох.
направлении оси оу. Любая прямая,
параллельная оси оу, пересекает границу
области не более, чем в двух точках.
Построим сечение цилиндрического тела
плоскостью, перпендикулярной оси ох.![]() .
В сечении получим криволинейную трапецию
АВС
.
В сечении получим криволинейную трапецию
АВС![]() ,
ограниченную линиями
,
ограниченную линиями![]() ,
где
,
где![]() ,Z=0,
,Z=0,![]() и
и![]() (рис.2). ПлощадьS(x)
этой трапеции находим с помощью
определенного интеграла
(рис.2). ПлощадьS(x)
этой трапеции находим с помощью
определенного интеграла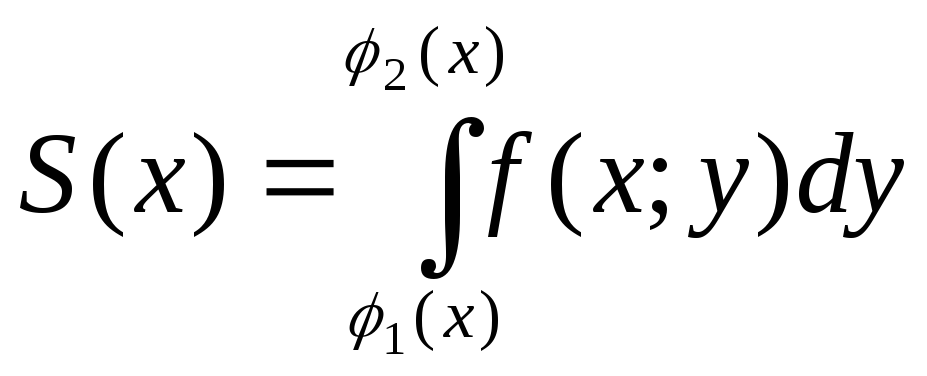 .
Теперь согласно методу параллельных
сечений искомый объем цилиндрического
тела может быть найден так:
.
Теперь согласно методу параллельных
сечений искомый объем цилиндрического
тела может быть найден так: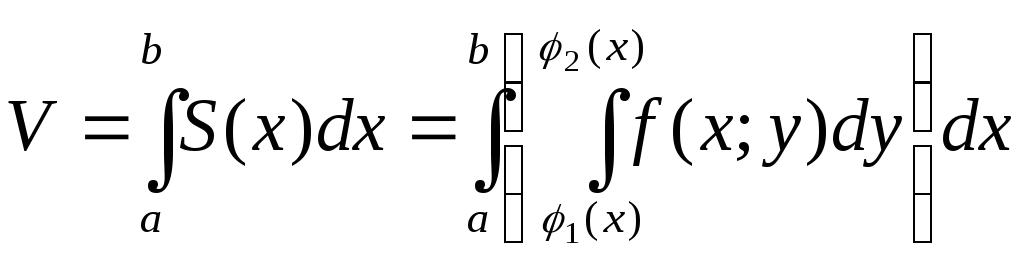 .
С другой стороны, выше мы показали, что
объем цилиндрического тела определяется
как двойной интеграл от функции
.
С другой стороны, выше мы показали, что
объем цилиндрического тела определяется
как двойной интеграл от функции![]() ≥0
по области
≥0
по области![]() .
Следовательно
.
Следовательно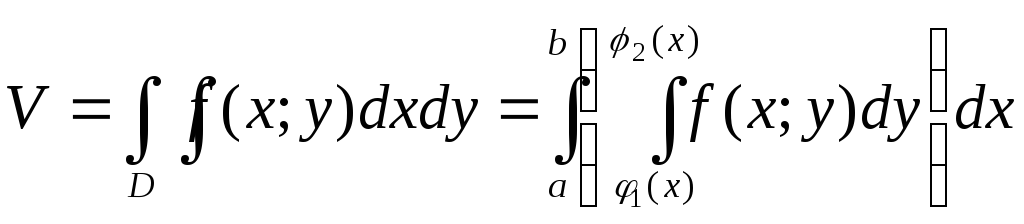 .
Это равенство обычно записывают в виде
:
.
Это равенство обычно записывают в виде
: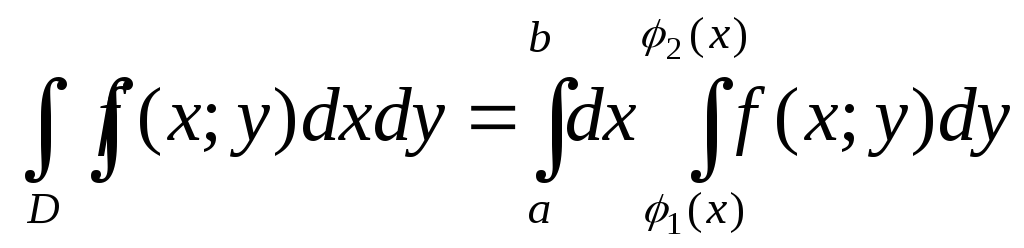 .
Полученная формула представляет собой
способ вычисления двойного интеграла.
Правую часть называют двукратным или
повторным интегралом функции
.
Полученная формула представляет собой
способ вычисления двойного интеграла.
Правую часть называют двукратным или
повторным интегралом функции![]() по области
по области![]() .
При этом
.
При этом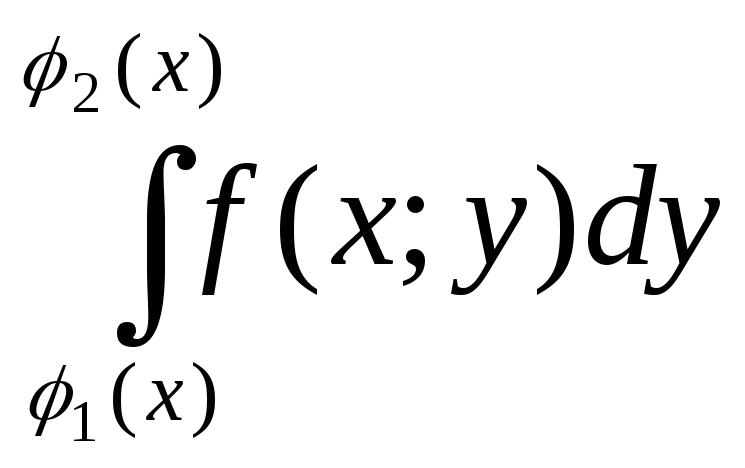 называют внутренним интегралом. Для
вычисления двукратного интеграла
сначала берем внутренний интеграл,
затем берем внешний. Т.е. результат
первого интегрирования интегрируем по
х в пределах от а до b.
называют внутренним интегралом. Для
вычисления двукратного интеграла
сначала берем внутренний интеграл,
затем берем внешний. Т.е. результат
первого интегрирования интегрируем по
х в пределах от а до b.
Если же область
![]() ограничена прямыми
ограничена прямыми![]() ,
,![]()
![]() ,
кривыми
,
кривыми![]() ,
,![]() (
(![]() )
для всех у. Т.е. область
)
для всех у. Т.е. область![]() правильна в направлении оси ох, то
рассекая тело плоскостью
правильна в направлении оси ох, то
рассекая тело плоскостью![]() получим
получим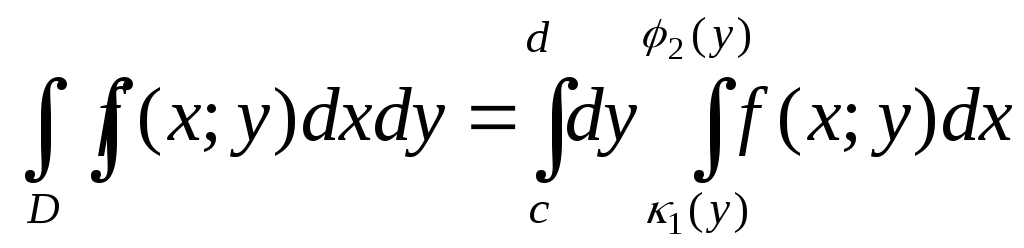 .
Здесь при вычислении внутреннего
интеграла, считаем
.
Здесь при вычислении внутреннего
интеграла, считаем![]() .
.
Пример.Вычислить![]() ,
где
,
где![]() ограничена линиями
ограничена линиями![]() ,
,![]() ,
,![]() .
.![]()
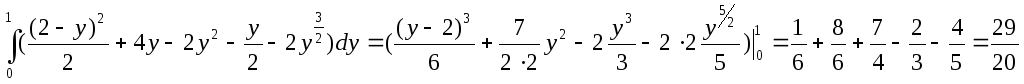 ;
;
4.5. Приложения двойного интеграла
Приведем некоторые примеры применения двойного интеграла.
Объем тела
Как уже говорилось, объем цилиндрического
тела можно найти по формуле
![]() ,
где
,
где![]() -
уравнение поверхности, ограничивающей
тело сверху.
-
уравнение поверхности, ограничивающей
тело сверху.
Площадь плоской фигуры
Если положить в формуле для объема тела
через двойной интеграл
![]() =1,
то цилиндрическое тело превратить в
прямой цилиндр с высотой Н=1. Объем такого
цилиндра численно равен, как известно,
площадиSоснования
=1,
то цилиндрическое тело превратить в
прямой цилиндр с высотой Н=1. Объем такого
цилиндра численно равен, как известно,
площадиSоснования![]() .
При этом получится формула для вычисления
площадиSобласти
.
При этом получится формула для вычисления
площадиSобласти![]()
![]() .
.
Масса плоской фигуры
Пусть дана плоская пластина
![]() с переменной плотностью γ, которую можно
записать как функцию
с переменной плотностью γ, которую можно
записать как функцию![]() .
.
Разобьем пластину на элементарные части
![]() ,
площади которых обозначим через
,
площади которых обозначим через![]() .
В каждой области
.
В каждой области![]() возьмем произвольную точку
возьмем произвольную точку![]() .
Если область
.
Если область![]() достаточно мала, то плотность в каждой
точке этой области
достаточно мала, то плотность в каждой
точке этой области![]() мало отличаются друг от друга. Считая
эту плотность в
мало отличаются друг от друга. Считая
эту плотность в![]() величиной постоянной мы можем найти
массу
величиной постоянной мы можем найти
массу![]() :
:![]() ,
а так как масса всей пластины
,
а так как масса всей пластины![]() ,
то можно записать
,
то можно записать![]() .
Точное значениеmполучим,
как предел этой суммы при
.
Точное значениеmполучим,
как предел этой суммы при![]() и
и![]()
![]() ,
т.е.
,
т.е.![]() .
.
Статические моменты и центр тяжести плоской фигуры
Статические моменты могут быть вычислены
с использованием раннее полученных
соотношений по следующим формулам:
![]() и
и![]() ,
а координаты центра масс фигуры по
формулам:
,
а координаты центра масс фигуры по
формулам:![]() и
и![]() .
.
