7.2. Тригонометрический ряд Фурье

С помощью так называемого тригонометрического ряда любую (практически) периодическую функцию можно представить в виде ряда, членами которого являются простые гармоники. Тригонометрическим рядом называется функциональный ряд вида , где действительные числаa₀…a_n, b_n (n=1,2…) называются коэффициентами ряда. Этот ряд можно записать в виде . Действительно, положив,, получимч.т.д., при этоми. Свободный член ряда записан в видедля единообразнополучающихся в дальнейшем формул.

Приведем соотношения, которые нам в дальнейшем пригодятся. Считая m и n целыми и положительными, найдем 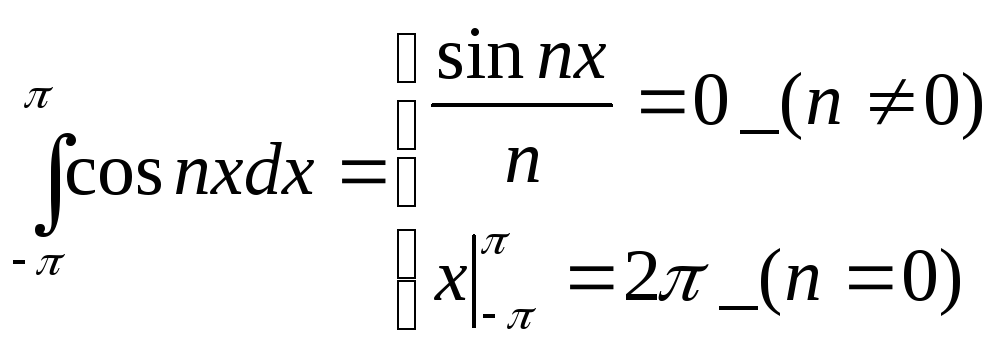(1),

, при любом n. (2)

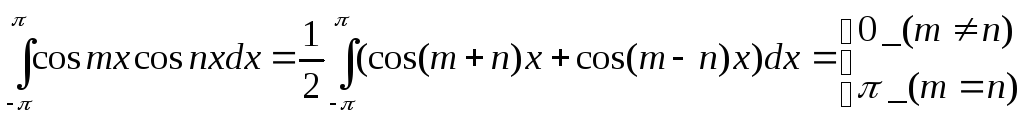(3)

(4)

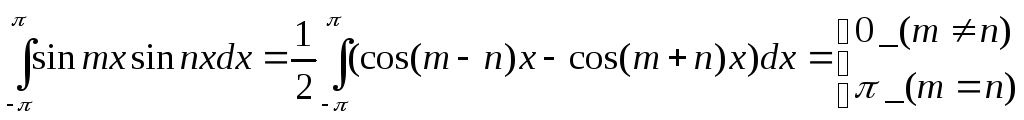(5)

Формулы (1-5) показывают, что функции ,, …,обладают свойствомортогональности – интеграл от произведения любых двух функций этого семейства на интервале, имеющий длину 2π, равен нулю. Кроме того, соотношения (1-5) справедливы и в случае, когда область интегрирования есть отрезок .

Пусть - произвольная периодическая функция с периодом 2π. Предположим, что функцияразлагается в тригонометрический ряд, т.е.является суммой ряда(6)

Так как функция и сумма ряда имеют период 2π, то ее можно рассматривать в любом промежутке длины 2π. В качестве основного промежутка возьмем отрезок, также удобно взять отрезоки предположим, что наш ряд на этом отрезке можно почленно интегрировать. Вычислим коэффициентыи. Для этого проинтегрируем обе части ряда в пределах от –π до π.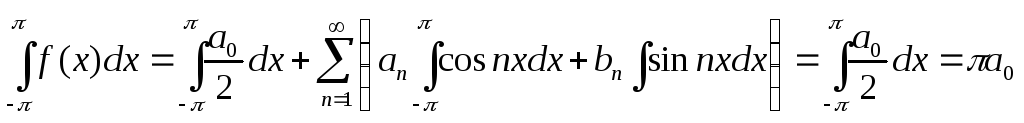интегралы от всех, кроме нулевого, членов ряда равны 0 в силу формул (1) и (2). Отсюда. Умножив обе части нашего ряда (6) наи проинтегрировав полученный ряд в пределах от –π до π., получим. В силу соотношений (1) (3) и (4) из этого соотношения приполучим, откуда,Аналогично, умножив соотношение (6) наи проинтегрировав почленно на отрезке, найдем,Числа, определяемые по приведенным выше формулам, называются коэффициентами Фурье функции, а тригонометрический ряд с такими коэффициентами рядом Фурье функции. Для интегрируемой на отрезкефункциизаписывают~и говорят, что функциисоответствует ее ряд Фурье. Если ряд Фурье сходится, его сумму обозначают.

7.3 Разложение в ряд Фурье 2π-периодических функций. Теорема Дирихле

Выясним условия, при которых знак соответствия (~) можно заменить знаком равенства (=), т.е. условия, при которых ряд Фурье функции сходится и имеет своей суммой как раз функцию.

Будем рассматривать функции , имеющие период. Такие функции называются 2π-периодическими. Сформулируем теорему, представляющую достаточное условие разложимости функции в ряд Фурье.

Теорема Дирихле. Пусть 2π-периодическая функция на отрезке удовлетворяет двум условиям:

1) кусочно-непрерывна, т.е. непрерывна или имеет конечное число точек разрыва 1 рода.

2) кусочно-монотонна, т.е. монотонна на всем отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна. Тогда соответствующей функцииряд Фурье сходится на этом отрезке и при этом:

1. В точках непрерывности функции сумма ряда совпадает с самой функцией.

2. В каждой точке разрыва функции сумма ряда равна. Т.е. равна среднеарифметическому пределу функциисправа и слева.

3. В точках и(на концах отрезка) сумма ряда равна.

Таким образом, если функция удовлетворяет условиям 1 и 2 теоремы Дирихле, то на отрезкеимеет место разложение, причем коэффициенты вычисляются по полученным ранее формулам для (). Это равенство может нарушиться только в точках разрыва функциии на концах отрезка. В силу периодичности исходной функции и суммы ряда Фурье может быть получено указанное разложение во всей области определения функции. Условиям Дирихле удовлетворяют большинство функций, которые встречаются в различных научных задачах. Однако существуют функции, не удовлетворяющие условиям Дирихле, но при этом разложимые в ряд Фурье, т.е. теорема Дирихле дает лишь достаточное условие разложения функции в ряд, но не необходимое.