9. Дифференцирование неявной функции

Функция Z= f(х; у) называется неявной, если она задается уравнением F(x,y,z)=0 неразрешенным относительноZ. Найдем частные производныефункцииZзаданной неявно. Для этого подставив в уравнение вместоZфункцию f(х;у) получим тождествоF(x,y, f(х,у))=0. Частные производные поxи yфункции, тождественно равной нулю, также равны нулю.

F(x,y, f (х, у)) ==0 (yсчитаем постоянным)

F(x,y, f (х, у)) ==0 (xсчитаем постоянным)

Откуда и

Пример: Найти частные производные функцииZзаданной уравнением.

Здесь F(x,y,z)=; ; ; . По формулам приведенным выше имеем:

и

9. Производная по направлению

Пусть функция двух переменных Z= f(x; у) задана в некоторой окрестности т. М (x,y). Рассмотрим некоторое направление, определяемое единичным вектором, где (см. рис.).

На прямой, проходящей по этому направлению через т. М возьмем т. М₁() так, что длинаотрезкаMM₁ равна . Приращение функцииf(M) определяется соотношением, гдесвязаны соотношениями. Предел отношенияприбудет называться производной функциив точкепо направлениюи обозначаться.

=

Если функция Zдифференцируема в точке, то ее приращение в этой точке с учетом соотношений дляможет быть записано в следующей форме.

поделив обе части на

и переходя к пределу при получим формулу для производной функции Z= f(х; у) по направлению:

9. Градиент

Рассмотрим функцию трех переменных дифференцируемой в некоторой точке.

Градиентом этой функции в точке М называется вектор, координаты которого равны соответственно частным производнымв этой точке. Для обозначения градиента используют символ.=.

.Градиент указывает направление наибыстрейшего роста функции в данной точке.

Поскольку единичный вектор имеет координаты (), то производная по направлению для случая функции трех переменных записывается в виде, т.е.имеет формулу скалярного произведения векторови. Перепишем последнюю формулу в следующем виде:

, где- угол между вектороми. Поскольку, то отсюда следует, что производная функции по направлению принимаетmaxзначение при=0, т.е. когда направление векторовисовпадают. При этом.Т.е., на самом деле градиент функции характеризует направление и величину максимальной скорости возрастания этой функции в точке.

9. Экстремум функции двух переменных

Понятия max,min, экстремума функции двух переменных аналогичны соответствующим понятиям функции одной переменной. Пусть функция Z= f(x; у) определена в некоторой областиDи т. Мпринадлежит к этой области. Точка Мназывается точкойmaxфункции Z= f(x; у), если существует такая δ-окрестность точки, что для каждой точки из этой окрестности выполняется неравенство. Аналогичным образом определяется и точкаmin, только знак неравенства при этом изменится. Значение функции в точкеmax(min) называется максимумом (минимумом). Максимум и минимум функции называются экстремумами.

9. Необходимые и достаточные условия экстремума

Теорема:(Необходимые условия экстремума). Если в точке Мдифференцируемая функция Z= f(x; у) имеет экстремум, то ее частные производные в этой точке равны нулю:,.

Доказательство: зафиксировав одну из переменныхxилиy, ревратим Z= f(x; у) в функцию одной переменной, для экстремума которой вышеописанные условия должны выполняться. Геометрически равенстваиозначают, что в точке экстремума функции Z= f(x; у), касательная плоскость к поверхности, изображающую функциюf(x,y)=Zпараллельна плоскостиOXY, т.к. уравнение касательной плоскости естьZ=Z_0. Точка, в которой частные производные первого порядка функции Z= f(x; у) равны нулю, т.е.,, называются стационарной точкой функции. Функция может иметь экстремум в точках, где хотя бы одна из частных производных не существует. НапримерZ=|-| имеетmaxв точкеO(0,0), но не имеет в этой точке производных.

Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками. В критических точках функция может иметь экстремум, а может и не иметь. Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума. Например, приZ=xyточкаO(0,0) является критической. Однако экстремума в ней функцияZ=xyне имеет. (Т.к. вIиIIIчетвертяхZ>0, а вIIиIV–Z<0). Таким образом для нахождения экстремумов функции в данной области необходимо подвергнуть каждую критическую точку функции дополнительному исследованию.

Теорема: (Достаточное условие экстремумов). Пусть в стационарной точкеи некоторой окрестности функция f(x; у) имеет непрерывные частные производные до 2^огопорядка включительно. Вычислим в точкезначения,и . Обозначим

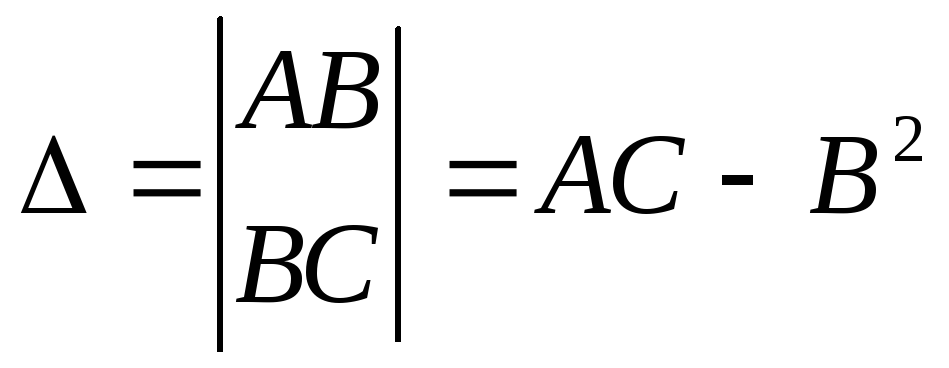
Тогда:

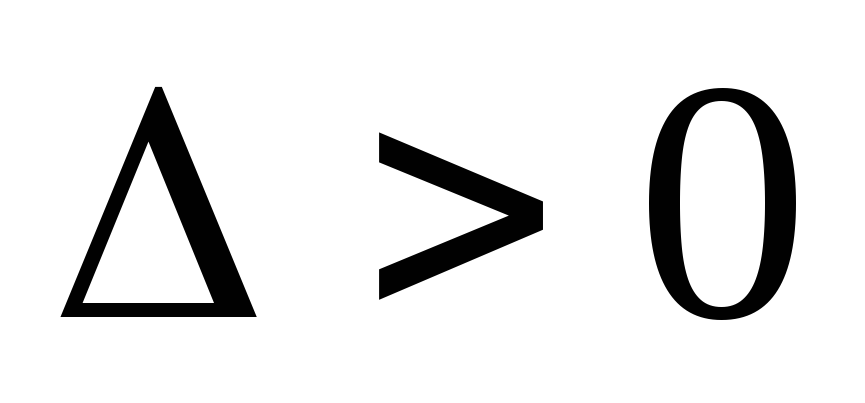1. если , то f(x; у) в точке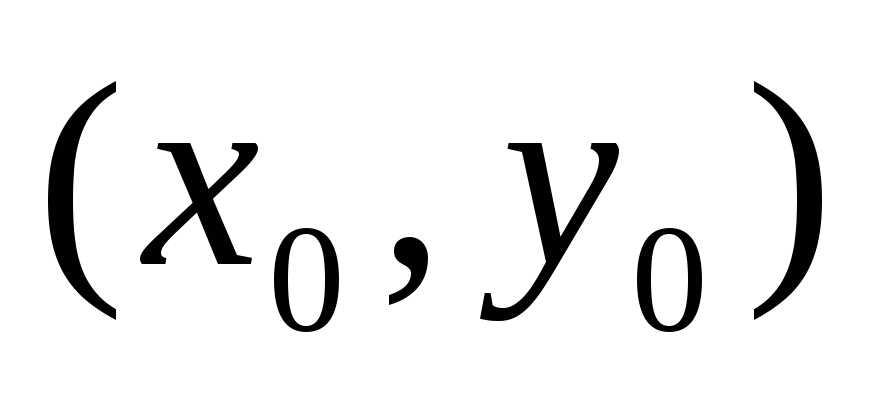имеет экстремумmax, если А<0 иmin, если А>0.

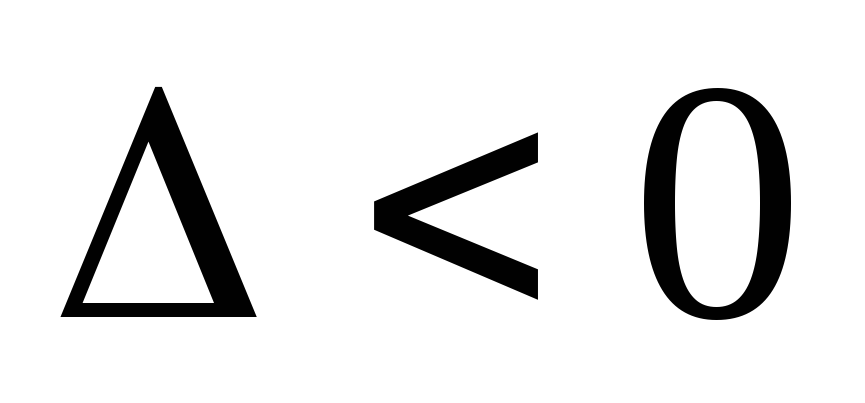2. если , то f(x; у) в точке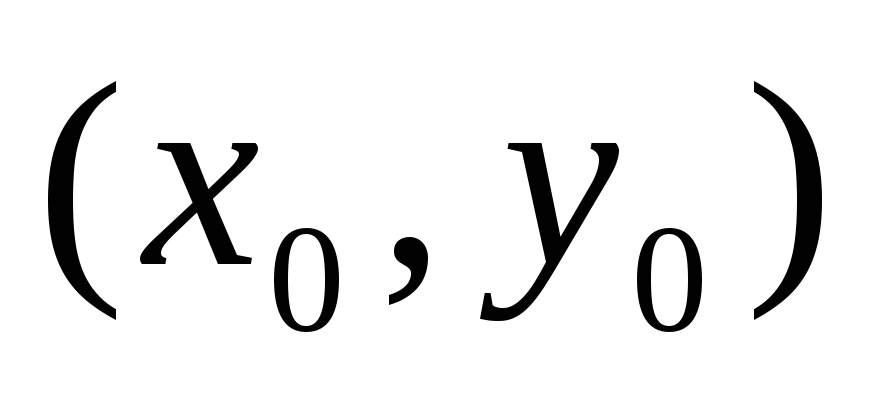экстремума не имеет.

В случае если , экстремум в точкеможет быть, а может и не быть. Необходимы дополнительные исследования.