4.6. Тройной интеграл. Основные понятия

Обобщением определенного интеграла на случай функции трех переменных является так называемый тройной интеграл. Теория тройного интеграла аналогична теории двойного интеграла, поэтому изложим ее в сокращенном виде.

Пусть в замкнутой области V пространства oxyzзадана непрерывная функция. Разбив область V сеткой поверхностей наnчастейи выбрав в каждой их них произвольную точкусоставим интегральную суммудля функциипо области V (∆V_i– объем элементарной областиV_i). Если предел интегральной суммы существует при неограниченном увеличении числаn таким образом, что каждаяV_i стягивается в точку, то его называют тройным интегралом от функции по области V и обозначают(или). Таким образом, по определению получаем. Здесь- элемент объема- диаметрi-области.

Теорема.Если функциянепрерывна в ограниченной замкнутой области V, то предел интегральной суммы приbсуществует и не зависит ни от способа разбиения области V на части, ни от выбора точекв них.

Тройной интеграл обладает теми же свойствами, что и двойной:

1) , где.

2) .

3) , если, а пересечениеV₁ иV₂ состоит из границы, их разделяющей.

4) , если в V. Если же в V, то и.

5) , так как в случаелюбая интегральная сумма имеет види численно равна объему тела.

6) Оценка тройного интеграла

, гдеmиM– соответственно наименьшее и наибольшее значение функциив области V.

7) Теорема о среднем значении

Если функция непрерывна в замкнутой области V, то в этой области существует такая точка, что, где V – объем тела.

4.7. Вычисление тройного интеграла.

Вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов. Пусть областью интегрирования является тело, ограниченное снизу поверхностью , сверху поверхностью, причеми(≤) – непрерывные функции в замкнутой области, являющейся проекцией тела на плоскость оху (рис.1). Будем считать область V правильной в направлении осиoz. Любая прямая, параллельная осиoz, пересекает границу области не более, чем в двух точках. Тогда для любой непрерывной в области V функцииимеет место соотношение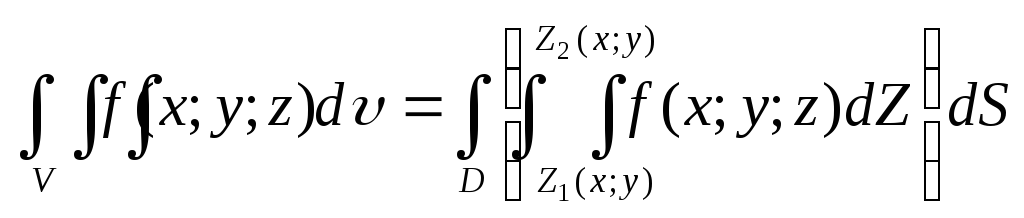, сводящее вычисление тройного интеграла к вычислению двойного интеграла от однократного (доказательство этого соотношения мы упускаем). При этом сначала вычисляется внутренний интеграл по переменнойZпри постоянных х и у в пределах измененияZ. Нижней границей интеграла является аппликата точки АК – точки входа прямой, параллельной осиoz, в область V, т.е., верхней границей аппликата точки В – точки выхода прямой из области V, т.е.. Результат вычисления этого интеграла есть функция двух переменных х и у. Если областьограничена линиями,(a<b),и, гдеи- непрерывные на отрезкефункции, причем≤(рис.2), то, переходя от тройного интеграла к повторному получаем формулу: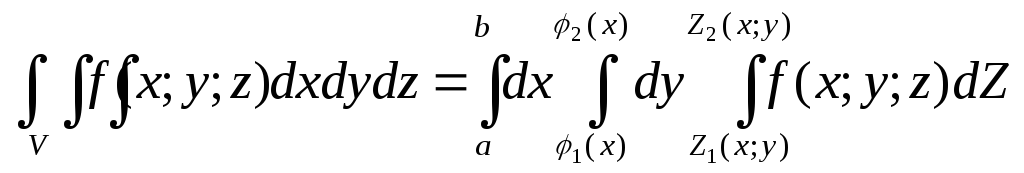. С помощью этого соотношения и производятся вычисления тройных интегралов.

П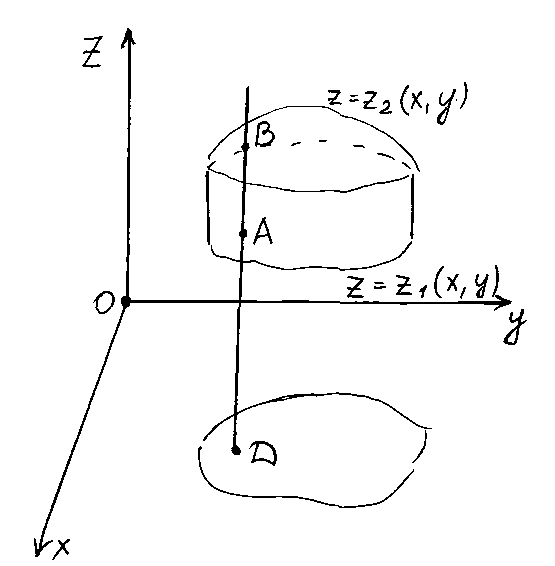ример.Вычислить, где V ограничивается плоскостями,,и(рис.1). Область V является правильной в направлении осиoz(как в направлении ох и оу). Ее проекция на плоскость оху является правильной в направлении оу и ох. Поэтому, применяя выше полученное соотношению имеем.