
- •Лекция 1 Функции нескольких переменных
- •Функция двух переменных
- •Предел функции
- •Непрерывность функции двух переменных
- •Производные и дифференциалы функции нескольких переменных
- •Частные производные высших порядков
- •Дифференцируемость и полный дифференциал функции
- •Дифференциалы высших порядков
- •Производная сложной функции. Полная производная
- •8.Инвариантность формы полного дифференциала
- •Дифференцирование неявной функции
- •Производная по направлению
- •Градиент
- •Экстремум функции двух переменных
- •Необходимые и достаточные условия экстремума
- •Лекции №№2,3
- •II. Неопределенный интеграл
- •2. Свойства неопределенного интеграла
- •3. Таблица основных неопределенных интегралов
- •4. Основные методы интегрирования
- •5. Интегрирование рациональных функций.
- •6. Интегрирование тригонометрических функций
- •7. Интегрирование иррациональных функций
- •Лекция 4
- •III. Определенный интеграл
- •Определение определенного интеграла
- •Геометрический смысл определенного интеграла
- •3) Работа переменной силы
- •Формулы Ньютона-Лейбница
- •Основные свойства определенного интеграла
- •Вычисление определенного интеграла
- •Несобственные интегралы
- •Лекция 5
- •7. Применение определенных интегралов для расчета геометрических и физических величин различного рода
- •7.1. Вычисление площадей плоских фигур
- •7.2 Вычисление длины дуги плоской кривой
- •7.3 Вычисление объема тела
- •8. Приближенное вычисление определенного интеграла
- •8.1. Формулы прямоугольников
- •8.2. Формула трапеций
- •8.3. Формула парабол (Симпсона)
- •Лекция 6,7
- •4. Кратные интегралы
- •4.1. Двойной интеграл. Основные понятия
- •4.2. Геометрический смысл двойного интеграла
- •4.3. Основные свойства двойного интеграла
- •4.4.Вычисление двойного интеграла
- •4.5. Приложения двойного интеграла
- •4.6. Тройной интеграл. Основные понятия
- •4.7. Вычисление тройного интеграла.
- •4.8. Приложения тройного интеграла
- •Лекция 8
- •V. Числовые ряды
- •5.1. Основные понятия
- •5.2. Необходимый признак сходимости числового ряда
- •5.3. Достаточные признаки сходимости знакопостоянных рядов
- •5.4. Признак Даламбера
- •5.5. Радикальный признак Коши
- •5.6. Интегральный признак Коши. Обобщенный гармонический ряд
- •5.7. Знакочередующиеся и знакопеременные ряды Признак Лейбница
- •Общий достаточный признак сходимости знакопеременных рядов
- •5.8. Абсолютная и условная сходимость числовых рядов
- •Лекция №9 Степенные ряды
- •1 Функциональные ряды
- •1.1 Основные понятия
- •2. Некоторые приложения степенных рядов
- •2.1. Приближенное вычисление значений функций
- •2.2. Приближенное вычисление определенных интегралов
- •Лекция №10
- •VII Ряды Фурье
- •7.1. Основные понятия
- •7.2. Тригонометрический ряд Фурье
- •7.3 Разложение в ряд Фурье 2π-периодических функций. Теорема Дирихле
- •7.4. Разложение в ряд Фурье четных и нечетных функций
- •7.5. Разложение в ряд Фурье функций произвольного периода
- •Лекция 11.
- •VIII. Дифференциальные уравнения (д.У.)
- •8.1. Общие сведения на основании понятия о д.У.
- •8.2. Дифференциальное уравнение первого порядка
- •2. Метод Лагранжа
- •Лекция 12
- •8.3.Дифференциальные уравнения высших порядков
- •1.Решение путем понижения порядка уравнения.
- •2.Линейные дифференциальные уравнения высших порядков.
- •8.4. Решение ду второго порядка с постоянными коэффициентами.
- •1.Решение лоду второго порядка с постоянными коэффициентами.
- •Лекция 13
- •2. Решение лоду n –го порядка с постоянными коэффициентами.
- •Линейные неоднородные дифференциальные уравнения (лнду)
- •1.Структура общего решения лнду второго порядка.
- •2.Метод вариации произвольных постоянных.
- •3.Решение лнду второго порядка с постоянными коэффициентами и правой частью специального вида.
- •4.Решение лнду n- го порядка с постоянными коэффициентами и правой специальной частью.
- •Лекция 14
- •2.Системы линейных ду с постоянными коэффициентами.
Лекция 4
III. Определенный интеграл
Определение определенного интеграла
Пусть в нашем распоряжении есть функция
![]() ,
определенная на отрезке
,
определенная на отрезке![]() .
.
Разобьем отрезок на n произвольных частей точками
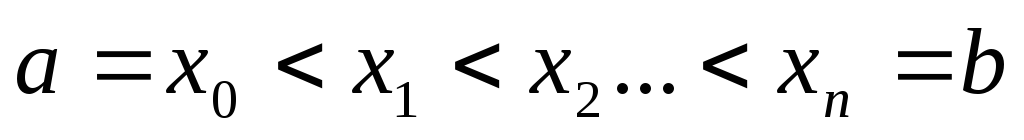 .
.В каждом из отрезков
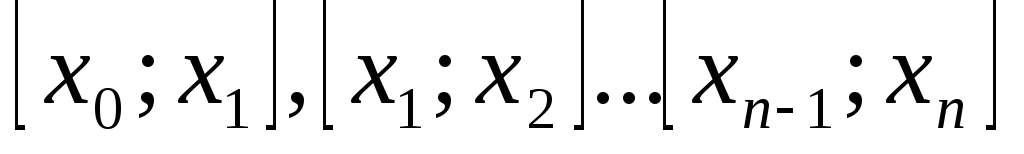 выберем произвольную точку
выберем произвольную точку ивычислим значение функции в
ней, т.е.величину
ивычислим значение функции в
ней, т.е.величину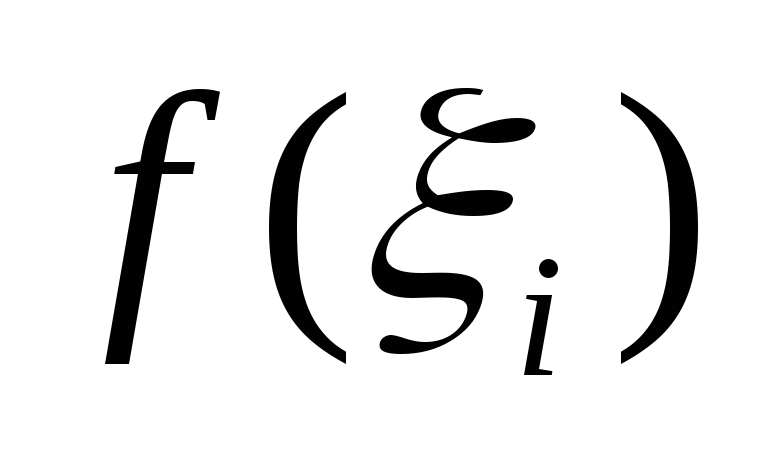
Умножим найденное значение функции
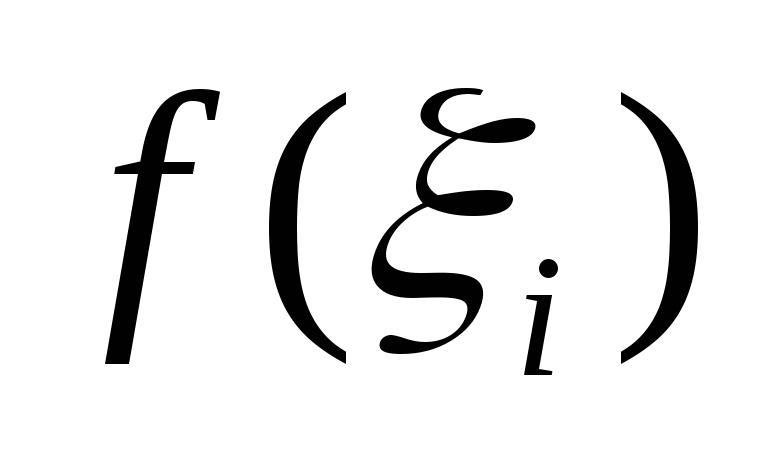 на
длину соответствующего отрезка
на
длину соответствующего отрезка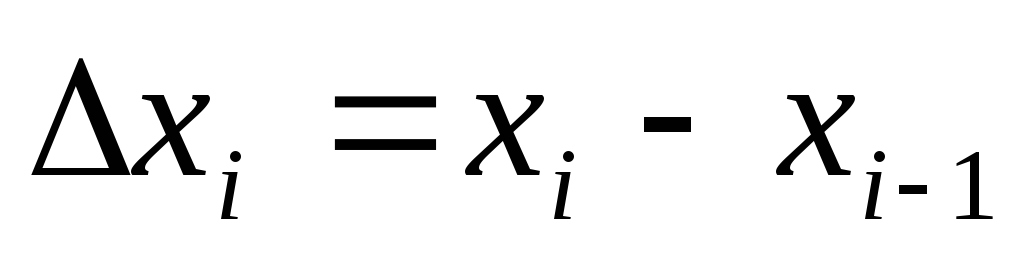 и получим величину
и получим величину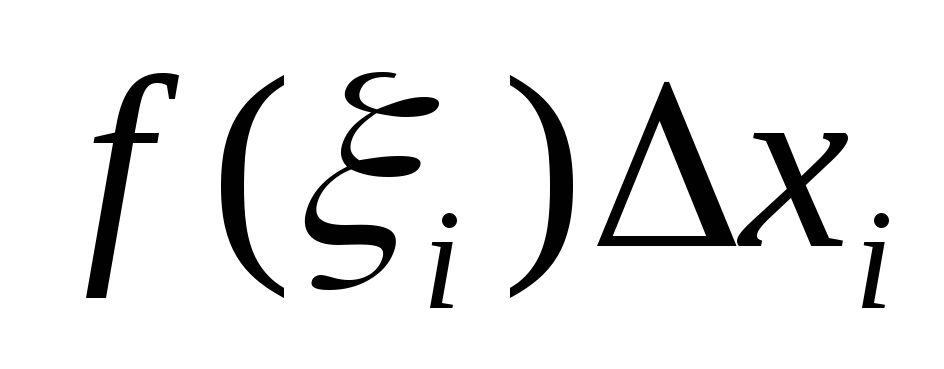 .
.Составим сумму Snвсех таких произведений
 .Сумма
подобного вида называется интегральной
суммой функции
.Сумма
подобного вида называется интегральной
суммой функции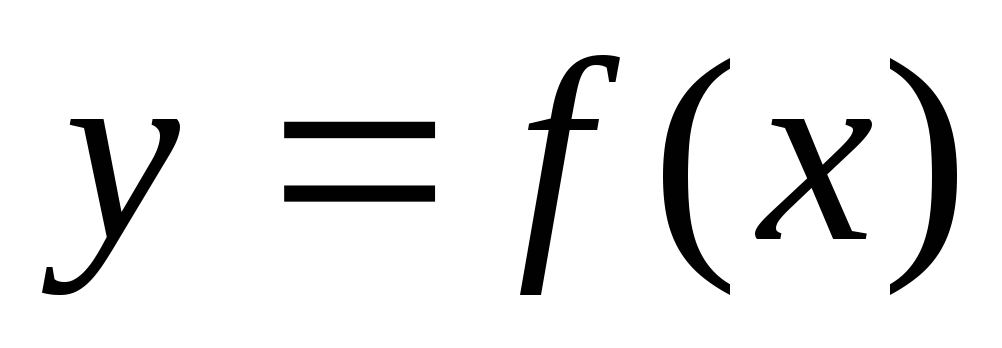 на отрезке
на отрезке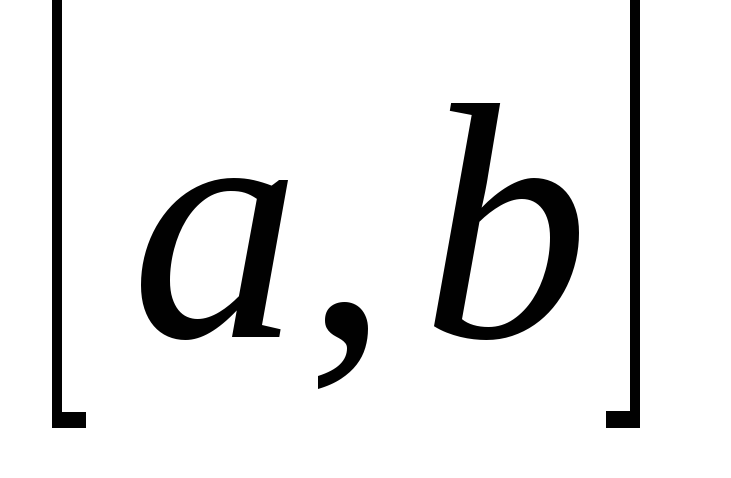 .
.Обозначим через
 длину наибольшего частичного отрезка
длину наибольшего частичного отрезка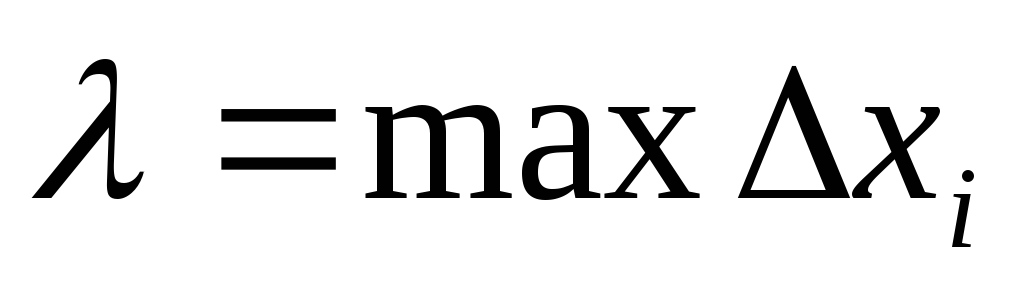 .
.Найдем предел интегральной суммы при условии
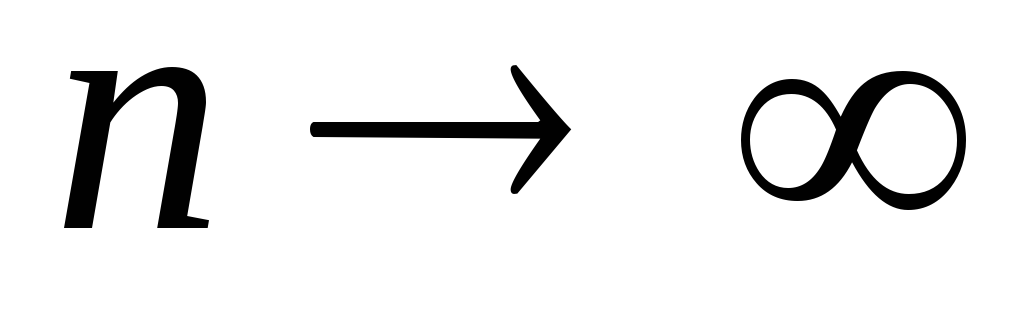 так, что
так, что .
.
Если при этом интегральная сумма Sn
имеет предел равныйI,
который не зависит от способа разбиения
отрезка![]() на частичные отрезки, ни от выбора точек
в них, то числоIназывается
определенным интегралом функции
на частичные отрезки, ни от выбора точек
в них, то числоIназывается
определенным интегралом функции![]() на отрезке
на отрезке![]() и обозначается
и обозначается![]() .
Таким образом,
.
Таким образом,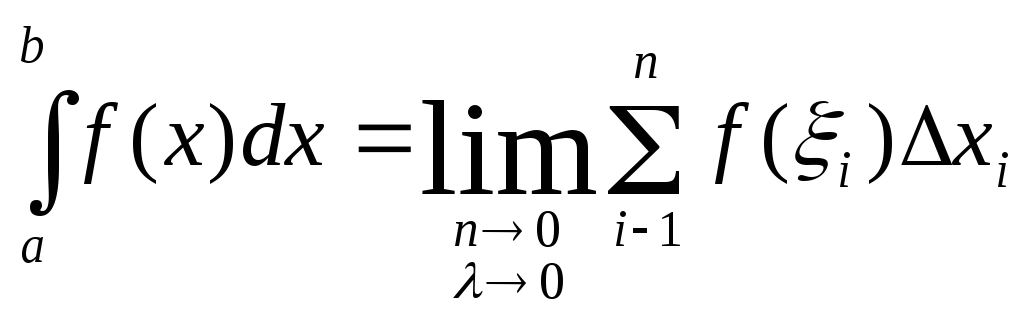 .
Числаaиbназываются нижними и верхними пределами
интегрирования,
.
Числаaиbназываются нижними и верхними пределами
интегрирования,![]() - подынтегральной функцией,
- подынтегральной функцией,![]() dx– подынтегральным выражением,x– переменной интегрирования,
dx– подынтегральным выражением,x– переменной интегрирования,![]() - областью интегрирования функции
- областью интегрирования функции![]() ,
для которой на отрезке
,
для которой на отрезке![]() существует определенный интеграл
существует определенный интеграл![]() ,
называется интегрируемой на этом
участке.
,
называется интегрируемой на этом
участке.
Теор. Коши. Если функция![]() непрерывна на отрезке
непрерывна на отрезке![]() ,
то определенный интеграл
,
то определенный интеграл![]() существует.
существует.
Непрерывность функции является достаточным условием ее интегрируемости. Однако, неопределенный интеграл может существовать и для некоторых разрывных функций, в частности для всякой ограниченной на отрезке функции, имеющей на нем конечное число точек разрыва.
Геометрический смысл определенного интеграла
Пусть на отрезке
![]() задана непрерывная функция
задана непрерывная функция![]() .
Нарисуем график этой функции. Фигура
ограниченная сверху графиком функции
.
Нарисуем график этой функции. Фигура
ограниченная сверху графиком функции![]() ,
снизу осьюox, сбоку линиямиx=aиx=bназывается криволинейной трапецией.
Найдем площадь этой трапеции. Для этого
отрезок
,
снизу осьюox, сбоку линиямиx=aиx=bназывается криволинейной трапецией.
Найдем площадь этой трапеции. Для этого
отрезок![]() разделим точками
разделим точками![]() наnчастей и т.д. повторяя
то, что мы делали выше, получим
наnчастей и т.д. повторяя
то, что мы делали выше, получим![]() - будет равна площади ступенчатой фигуры
и приближено площади криволинейной
трапеции
- будет равна площади ступенчатой фигуры
и приближено площади криволинейной
трапеции
![]()
С уменьшением величины
![]() точность приближенияSкриволинейной трапеции кSпрямоугольной. Точность записанного
выше соотношения возрастает. Поэтому
за точное значение площади криволинейной
трапеции принимается пределS,
к которому стремится площадь ступенчатой
фигурыSn,
когда
точность приближенияSкриволинейной трапеции кSпрямоугольной. Точность записанного
выше соотношения возрастает. Поэтому
за точное значение площади криволинейной
трапеции принимается пределS,
к которому стремится площадь ступенчатой
фигурыSn,
когда![]() так,
что
так,
что![]() при
при![]() .
.
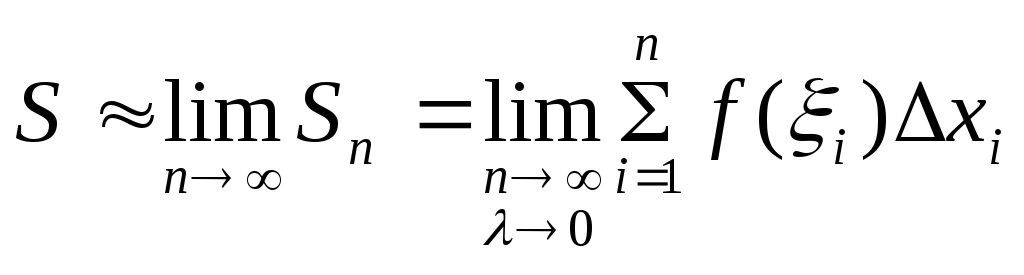 ,
то есть
,
то есть![]() .
.
Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции. В этом и состоит геометрический смысл определенного интеграла.
3) Работа переменной силы
Пусть материальная точка перемещается
под действием силы F,
направленной вдоль осиOXи имеющей переменную величину![]() .
Найдем работу по перемещению точки М
на
.
Найдем работу по перемещению точки М
на![]() .
.![]() .
Для определения приближенного значения
работы на всем участке
.
Для определения приближенного значения
работы на всем участке![]() ,
нам надо произвести суммирование на
всем отрезке.
,
нам надо произвести суммирование на
всем отрезке.
![]() .
.
Точность этого равенства возрастает с
уменьшением
![]() и увеличениемn. Поэтому
за точное значение работы принимается
предел этой суммы
и увеличениемn. Поэтому
за точное значение работы принимается
предел этой суммы
![]()
![]() .
.
Формулы Ньютона-Лейбница
Пусть
![]() - функция, интегрируемая на
- функция, интегрируемая на![]() .
.
Теорема: Если![]() - непрерывна на отрезке
- непрерывна на отрезке![]() и
и![]() ее первообразная на отрезке
ее первообразная на отрезке![]() (
(![]() =
=![]() ),
то имеет место соотношение
),
то имеет место соотношение![]()
![]() .
.
Доказательство:
Для этого отрезок
![]() разделим точками
разделим точками![]() наnотрезков. Введем
средние точки для каждого из отрезков
наnотрезков. Введем
средние точки для каждого из отрезков![]() .
Рассмотрим соотношение
.
Рассмотрим соотношение![]() .
.
Преобразуем каждую разность в скобках
по формуле Лагранже
![]() .
.
Получим:
![]() ,
,
т.е.
![]()
![]() .
Т.к.
.
Т.к.![]() непрерывна на
непрерывна на![]() ,
то она интегрируема на
,
то она интегрируема на![]() ,
поэтому перейдя к пределу при
,
поэтому перейдя к пределу при![]() .
Получим:
.
Получим:
![]()
![]() .
.
Формула Ньютона-Лейбница позволяет
получить удобный способ вычисления
определенных интегралов. Чтобы вычислить
определенный интеграл от неправильной
функции на отрезке
![]() надо найти ее первообразную функцию
надо найти ее первообразную функцию![]() и взять разность
и взять разность![]() значений этой первообразной на концах
отрезка
значений этой первообразной на концах
отрезка![]() .
.
Пример:
![]() .
.
