
- •Лекция 1 Функции нескольких переменных
- •Функция двух переменных
- •Предел функции
- •Непрерывность функции двух переменных
- •Производные и дифференциалы функции нескольких переменных
- •Частные производные высших порядков
- •Дифференцируемость и полный дифференциал функции
- •Дифференциалы высших порядков
- •Производная сложной функции. Полная производная
- •8.Инвариантность формы полного дифференциала
- •Дифференцирование неявной функции
- •Производная по направлению
- •Градиент
- •Экстремум функции двух переменных
- •Необходимые и достаточные условия экстремума
- •Лекции №№2,3
- •II. Неопределенный интеграл
- •2. Свойства неопределенного интеграла
- •3. Таблица основных неопределенных интегралов
- •4. Основные методы интегрирования
- •5. Интегрирование рациональных функций.
- •6. Интегрирование тригонометрических функций
- •7. Интегрирование иррациональных функций
- •Лекция 4
- •III. Определенный интеграл
- •Определение определенного интеграла
- •Геометрический смысл определенного интеграла
- •3) Работа переменной силы
- •Формулы Ньютона-Лейбница
- •Основные свойства определенного интеграла
- •Вычисление определенного интеграла
- •Несобственные интегралы
- •Лекция 5
- •7. Применение определенных интегралов для расчета геометрических и физических величин различного рода
- •7.1. Вычисление площадей плоских фигур
- •7.2 Вычисление длины дуги плоской кривой
- •7.3 Вычисление объема тела
- •8. Приближенное вычисление определенного интеграла
- •8.1. Формулы прямоугольников
- •8.2. Формула трапеций
- •8.3. Формула парабол (Симпсона)
- •Лекция 6,7
- •4. Кратные интегралы
- •4.1. Двойной интеграл. Основные понятия
- •4.2. Геометрический смысл двойного интеграла
- •4.3. Основные свойства двойного интеграла
- •4.4.Вычисление двойного интеграла
- •4.5. Приложения двойного интеграла
- •4.6. Тройной интеграл. Основные понятия
- •4.7. Вычисление тройного интеграла.
- •4.8. Приложения тройного интеграла
- •Лекция 8
- •V. Числовые ряды
- •5.1. Основные понятия
- •5.2. Необходимый признак сходимости числового ряда
- •5.3. Достаточные признаки сходимости знакопостоянных рядов
- •5.4. Признак Даламбера
- •5.5. Радикальный признак Коши
- •5.6. Интегральный признак Коши. Обобщенный гармонический ряд
- •5.7. Знакочередующиеся и знакопеременные ряды Признак Лейбница
- •Общий достаточный признак сходимости знакопеременных рядов
- •5.8. Абсолютная и условная сходимость числовых рядов
- •Лекция №9 Степенные ряды
- •1 Функциональные ряды
- •1.1 Основные понятия
- •2. Некоторые приложения степенных рядов
- •2.1. Приближенное вычисление значений функций
- •2.2. Приближенное вычисление определенных интегралов
- •Лекция №10
- •VII Ряды Фурье
- •7.1. Основные понятия
- •7.2. Тригонометрический ряд Фурье
- •7.3 Разложение в ряд Фурье 2π-периодических функций. Теорема Дирихле
- •7.4. Разложение в ряд Фурье четных и нечетных функций
- •7.5. Разложение в ряд Фурье функций произвольного периода
- •Лекция 11.
- •VIII. Дифференциальные уравнения (д.У.)
- •8.1. Общие сведения на основании понятия о д.У.
- •8.2. Дифференциальное уравнение первого порядка
- •2. Метод Лагранжа
- •Лекция 12
- •8.3.Дифференциальные уравнения высших порядков
- •1.Решение путем понижения порядка уравнения.
- •2.Линейные дифференциальные уравнения высших порядков.
- •8.4. Решение ду второго порядка с постоянными коэффициентами.
- •1.Решение лоду второго порядка с постоянными коэффициентами.
- •Лекция 13
- •2. Решение лоду n –го порядка с постоянными коэффициентами.
- •Линейные неоднородные дифференциальные уравнения (лнду)
- •1.Структура общего решения лнду второго порядка.
- •2.Метод вариации произвольных постоянных.
- •3.Решение лнду второго порядка с постоянными коэффициентами и правой частью специального вида.
- •4.Решение лнду n- го порядка с постоянными коэффициентами и правой специальной частью.
- •Лекция 14
- •2.Системы линейных ду с постоянными коэффициентами.
1.Решение путем понижения порядка уравнения.
Суть этого метода состоит в том, что с помощью замены переменной (подстановки) данное ДУ сводится к уравнению порядок которого ниже.
Рассмотрим три вида уравнений решенных таким способом.
1)
![]()
Порядок этого уравнения можно легко
понизить введя
![]() такую, что
такую, что![]() ,
тогда
,
тогда![]() и после подстановки получим
и после подстановки получим![]() ,
,
решив его, найдем
![]() и тогда решая
и тогда решая![]() получим общее решение первоначального
уравнения
получим общее решение первоначального
уравнения![]() .
.
На практике можно понизить порядок
путем последовательного интегрирования
уравнения. Т.к.
![]() ,
то наше уравнение можно записать в виде
,
то наше уравнение можно записать в виде![]() ,
тогда интегрируя уравнение
,
тогда интегрируя уравнение![]() получим
получим![]() или
или![]()
Интегрируя последнее уравнение по х
найдем
![]()
т.е.
![]() - общее решение данного уравнения.
- общее решение данного уравнения.
Если дано уравнение
![]() ,то
проинтегрировав его последовательноnраз ,найдем общее решение
уравнения:
,то
проинтегрировав его последовательноnраз ,найдем общее решение
уравнения:
![]()
Пример:![]()
![]()
![]()
![]() -
общее решение.
-
общее решение.
2)
![]() .
.
Обозначим
![]() ,где
,где![]() - новая неизвестная функция. Тогда
- новая неизвестная функция. Тогда![]() и наше уравнение примет вид:
и наше уравнение примет вид:![]() .
Пусть
.
Пусть![]() - общее решение полученного уравнения.
Тогда заменяя Р на
- общее решение полученного уравнения.
Тогда заменяя Р на![]() получаем
получаем![]() .
Это уравнение можно интегрировать
.
Это уравнение можно интегрировать
![]() . Частным случаем рассмотренного
уравнения является
. Частным случаем рассмотренного
уравнения является![]() .
Оно интегрируется тем же способом :
.
Оно интегрируется тем же способом :![]() .
Получаем
.
Получаем![]() с разделяющимися переменными.
с разделяющимися переменными.
Если задано уравнение вида
![]() б то его порядок можно понизить наkединиц положив
б то его порядок можно понизить наkединиц положив![]() .Тогда
.Тогда![]() и уравнение примет вид
и уравнение примет вид![]()
Частным случаем последнего уравнения
служит
![]() или
или![]() .
С помощью замены
.
С помощью замены![]() это уравнение сводится к ДУ первого
порядка.
это уравнение сводится к ДУ первого
порядка.
Пример: ![]() Полагая
Полагая![]() получим
получим![]() - уравнение с разделяющимися переменными
- уравнение с разделяющимися переменными![]() интегрируя получим
интегрируя получим![]() ,
возвращаясь к исходной переменной
,
возвращаясь к исходной переменной
![]()
3) Уравнение вида
![]() .
.
Для понижения порядка этого уравнения
введем функцию
![]() зависящую
от переменной
зависящую
от переменной![]() ,полагая
,полагая![]() .
Дифференцируя это равенство по
.
Дифференцируя это равенство по![]() с учетом, что
с учетом, что![]() получим
получим![]() , т.е.
, т.е.![]()
тогда после подстановки получим
![]() .
Пусть
.
Пусть![]() является общим решением этого уравнения.
Заменяя функцию
является общим решением этого уравнения.
Заменяя функцию![]() на
на![]() получаем
получаем![]() - ДУ с разделяющимися переменными.
Интегрируя его найдем общий интеграл
нашего уравнения.
- ДУ с разделяющимися переменными.
Интегрируя его найдем общий интеграл
нашего уравнения.![]() . Частным случаем ДУ является уравнение
. Частным случаем ДУ является уравнение![]() .Это
уравнение решается при помощи аналогичной
подстановки
.Это
уравнение решается при помощи аналогичной
подстановки![]() и
и![]() .
.
Точно также решается уравнение
![]() ,
его порядок понижается на единицу
заменой
,
его порядок понижается на единицу
заменой![]() по правилу дифференцирования сложной
функции
по правилу дифференцирования сложной
функции![]() .
.
![]() и т.д.
и т.д.
2.Линейные дифференциальные уравнения высших порядков.
Уравнение вида
![]() где
где![]() -
-
заданные функции (от![]() )
называютлинейным ДУ n-го
порядка .
)
называютлинейным ДУ n-го
порядка .
Оно содержит искомую функцию
![]() и
все ее производные лишь в первой степени.
Функции
и
все ее производные лишь в первой степени.
Функции![]() называются коэффициентами уравнения,
а
называются коэффициентами уравнения,
а![]() - его свободным членом .Если
- его свободным членом .Если![]() то уравнение называетсяоднородным
линейным дифференциальным уравнением.
Если
то уравнение называетсяоднородным
линейным дифференциальным уравнением.
Если![]() ,
то уравнение называетсянеоднородным.
,
то уравнение называетсянеоднородным.
Разделив уравнение на
![]() и обозначив
и обозначив![]()
можно записать уравнение в виде приведенного уравнения
![]() (10)
(10)
В дальнейшем будем рассматривать
уравнения типа (10) считая, что свободный
член и коэффициенты являются непрерывными
функциями ( на некотором интервале
![]() .
.
Линейные однородные ДУ второго порядка
Рассмотрим линейное однородное дифференциальное уравнение (ЛОДУ) второго
порядка
![]() (11)
(11)
Теорема 3 Если функции![]() и
и![]() являются частными решениями уравнения
(11) , то решением этого уравнения является
также функция
являются частными решениями уравнения
(11) , то решением этого уравнения является
также функция![]() , где
, где![]() и
и![]() произвольные постоянные.
произвольные постоянные.
Из теоремы вытекает, что если
![]() и
и![]() - решения уравнения (11),то решениями
этого уравнения будут также функции
- решения уравнения (11),то решениями
этого уравнения будут также функции![]()
![]() и
и![]() .
Решение содержит две постоянные величины
.
Решение содержит две постоянные величины![]() и
и![]() .Возникает
вопрос : будет ли это решение общим
решением уравнения (11)? Для ответа на
этот вопрос необходимо ввести понятие
линейной зависимости и линейной
независимости функций.
.Возникает
вопрос : будет ли это решение общим
решением уравнения (11)? Для ответа на
этот вопрос необходимо ввести понятие
линейной зависимости и линейной
независимости функций.
Функции
![]() и
и![]() называются линейно независимыми на
интервале
называются линейно независимыми на
интервале![]() если равенство
если равенство
![]() (12)
(12)
выполняется тогда и только тогда , когда
![]() .Если
хотя бы одно из чисел
.Если
хотя бы одно из чисел![]() или
или
![]() отличны
от нуля и равенство (12) выполняется ,то
функции
отличны
от нуля и равенство (12) выполняется ,то
функции![]() и
и![]() называютсялинейно зависимымина
называютсялинейно зависимымина![]() .Очевидно,
что функции
.Очевидно,
что функции![]() и
и![]() линейно зависимы, тогда и только тогда
когда они пропорциональны т.е. для всех
линейно зависимы, тогда и только тогда
когда они пропорциональны т.е. для всех![]() выполняется равенство
выполняется равенство![]() или
или![]() ,
где
,
где![]() .
.
Например, функции
![]() и
и![]() линейно зависимы, т.к.
линейно зависимы, т.к.![]() а
а![]() и
и![]() линейно независимы т.к.
линейно независимы т.к.![]() .
.
Оказывается, что совокупность любых
двух линейно независимых на интервале
![]() частных решений
частных решений![]() и
и![]() ЛОДУ второго порядка определяетфундаментальную систему решений этого уравнения: любое произвольное
решение может быть получено как комбинация
ЛОДУ второго порядка определяетфундаментальную систему решений этого уравнения: любое произвольное
решение может быть получено как комбинация![]() .
.
Теперь можно сформулировать при каких условиях только что приведенная комбинация будет общим решением уравнения (11).
Теорема 4 ( Структура общего решения ЛОДУ второго порядка)
Если два частных решения
![]() и
и![]() ЛОДУ (11) образуют на интервале
ЛОДУ (11) образуют на интервале![]() фундаментальную систему, то общим
решением этого уравнения является
функция
фундаментальную систему, то общим
решением этого уравнения является
функция![]() (12)
(12)
где
![]() - произвольныеconst.
- произвольныеconst.
Согласно теореме 3 функция (12) является решением уравнения (11).Поэтому остается доказать, что это решение общее, т.е. что из него можно выделить единственное частное решение, удовлетворяющее заданным начальным условиям
![]() где
где
![]() .
.
Это легко можно доказать, но мы этого делать не будем.
Линейные однородные ДУ n- го порядка.
Полученные выше результаты можно распространить на линейные однородные дифференциальные уравнения n-го порядка, имеющие вид
![]() (13)
(13)
1. Если функция
![]() является частным решением уравнения
(13), то его решением является и функция
является частным решением уравнения
(13), то его решением является и функция![]()
![]() .
.
2. Функции
![]() называются линейно независимыми на
называются линейно независимыми на![]() ,
если равенство
,
если равенство![]() выполняется лишь в случае, когда все
числа
выполняется лишь в случае, когда все
числа![]() ,
в противном случае (если хотя бы одно
из чисел
,
в противном случае (если хотя бы одно
из чисел![]() не равно нулю) функции
не равно нулю) функции![]() -
-
линейно зависимы.
3. Частные решения
![]() уравнения (13) образуютфундаментальную
систему решений на
уравнения (13) образуютфундаментальную
систему решений на![]() ,
если они линейно независимые решения
в этом промежутке.
,
если они линейно независимые решения
в этом промежутке.
Общее решение ЛОДУ(13) имеет вид
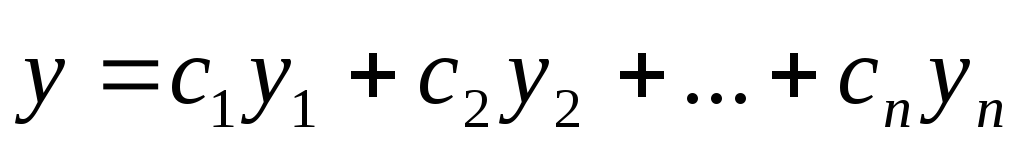 ,
где
,
где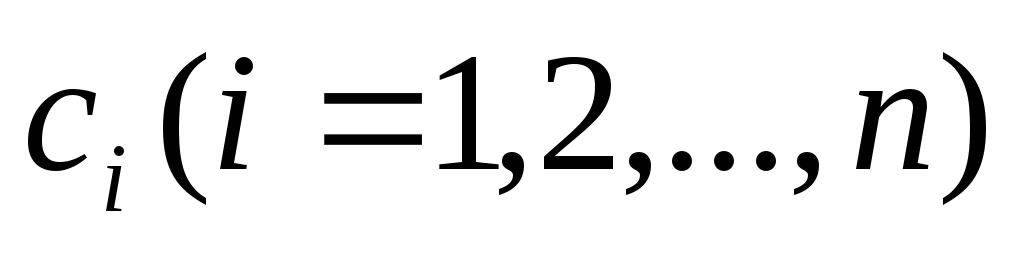 -
произвольные постоянные,
-
произвольные постоянные, - частные решения уравнения (13), образующие
фундаментальную систему.
- частные решения уравнения (13), образующие
фундаментальную систему.
