7.4. Разложение в ряд Фурье четных и нечетных функций

Если разлагаемая на отрезке функцияявляется четной или нечетной, то это отражается на формулах коэффициентов Фурье и на вид самого ряда. Если функциячетная, то ее ряд Фурье имеет вид(1), гдеи.

Если функция нечетная, то ее ряд Фурье имеет вид(2), где.

Доказательство. Как известно, если интегрируема на симметричном отрезке, то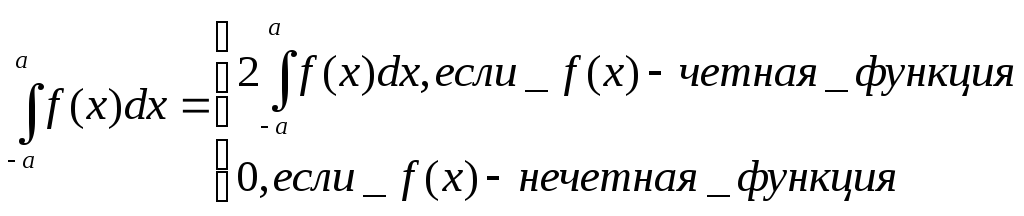. Если функция- четная, то- четная функция, а- нечетная функция.

Если же - нечетная функция, то, очевидно, функция- нечетная, а- четная. С учетом записанного соотношения из формул, ранее записанных дляполучаем формулы (1) и (2).

7.5. Разложение в ряд Фурье функций произвольного периода

Разлагать в ряд Фурье можно и периодические функции с периодом, отличным от 2π.

Пусть функция , определенная на отрезкеимеет период 2e , гдеe – произвольное положительное число) и удовлетворяет на этом отрезке условиям Дирихле. Сделав подстановку , данную функциюпреобразуем в функцию, которая определена на отрезкеи имеет период. Действительно, если, то, если, тои приимеем, т.е.. Разложение функциив ряд Фурье на отрезкеимеет вид, где(),().

Возвращаясь к переменной и заметив, что,, получим, где() ,().

Полученный ряд с коэффициентами, вычисляемые по выше записанным формулам, называется рядом Фурье для функции с периодом.

Все теоремы, имеющие место для рядов Фурье 2π-периодических функций, остаются в силе и для рядов Фурье функций, период которых . В частности, еслина отрезкечетная, то ее ряд Фурье имеет вид, где,,Если- нечетная функция, то, где,

Пример. Разложить функцию на интервалев ряд Фурье.

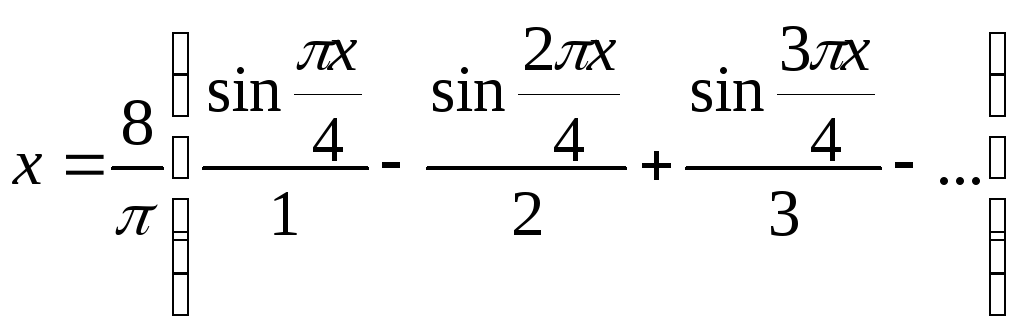Данная функция нечетная, удовлетворяет условиям Дирихле. По полученным только что формулам при получаем, где,Вычислим:,Таким образом,, для.

Лекция 11.

VIII. Дифференциальные уравнения (д.У.)

8.1. Общие сведения на основании понятия о д.У.

При решении различных задач в различных областях науки, в том числе в экономике, часто используют математические модели, при описании которых применяют уравнения, связывающие независимую переменную, искомую функцию и ее производные. Такие уравнения и называются дифференциальными. Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество. Так решением уравнения является функция– первообразная для функции.

Если искомая неизвестная функция зависит от одной переменной, то Д.У. называют обыкновенным, в противном случае Д.У. в частых производных. Далее будем рассматривать только обыкновенные Д.У. наивысший порядок производной, входящей в Д.У. называется порядком этого уравнения (например - обыкновенное уравнение четвертого порядка). Процесс нахождения решения Д.У. называется его интегрированием.

В качестве примера решения задач с использованием Д.У. можно, например, рассмотреть уравнение Циолковского. Обозначим скорость ракеты в некоторый момент времени череза массу- . пусть в этот момент времени включается двигатель, причем скорость выхлопных газов равна. Через времямасса ракеты уменьшается и станет равной, а скорость увеличится и станет равной. Сравним импульс системы ракеты + выхлопные газы в моменты времении. Первый равен, второй– импульс выхлопных газов. Итоговое уравнение примет вид (согласно закону сохранения импульса).

Пренебрегая бесконечно малой второго порядка , получим:

или – это дифференциальное уравнение с разделенными переменными. Решая его методом интегрирования получим, считая. Получим. Эта формула определяет изменение скорости ракеты в зависимости от изменения ее массы (формула Циолковского).