8.2. Формула трапеций

Эту формулу получают аналогично формуле прямоугольников. Только на каждом частичном отрезке криволинейная трапеция заменяется обычной.

Разобьем отрезок наравных частей с длиной. Абсциссы точек деления. Пустьсоответствующие им ординаты графика функции, тогда расчетные формулы для этих значений примут вид:,. Заменим кривуюломаной линией, звенья которой соединяют концы ординати. Тогда площадь криволинейной трапеции с основанием,и высотой:

или- это формула трапеций. Абсолютная погрешностьприближения, полученного по формуле трапеций, оценивается с помощью формулы:

, где- максимальное значение.

8.3. Формула парабол (Симпсона)

Если заменить график функции на каждом отрезкене отрезками прямых, как в случае формулы трапеции, а дугами парабол, то получим более точную формулу вычисления интеграла.

Выводить мы ее не будем, а ограничимся записью конечного выражения:

- это так называемая формула Симпсона.

Абсолютная погрешность оценивается соотношением, где- максимальное значение.

Лекция 6,7

4. Кратные интегралы

4.1. Двойной интеграл. Основные понятия

Обобщением определенного интеграла на случай функции двух переменных является так называемый двойной интеграл.

П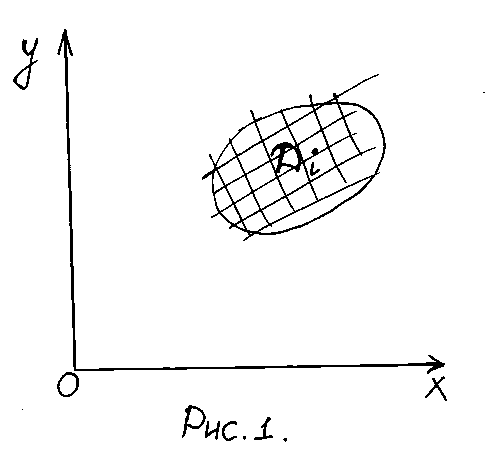усть в замкнутой областиплоскостизадана непрерывная функция. Разобьем областьнаnэлементарных областей(рис.1), площади которых обозначим через, а диаметры (наибольшие расстояния между точками области) – через. В каждой областивыберем произвольную точку, умножим значениефункции в этой точке наи составим сумму всех таких произведений:. Эта сумма называется интегральной суммойв области. Рассмотрим предел интегральной суммы, когдаnстремится к бесконечности таким образом, что. Если этот предел существует и не зависит ни от способа разбиения областина части, ни от выбора точек в них, то он называется двойным интегралом от функциипо областии обозначаетсяили. Таким образом двойной интеграл определяется равенством. В этом случае функцияназывается интегрируемой в области,- область интегрирования; х, у – переменные интегрирования,dxdy(илиdS) элемент площади.

Для всякой ли функции существует двойной интеграл? Ответ дает следующая теорема:

Теорема.(Достаточное условие интегрируемости функции) Если функциянепрерывна в замкнутой области, то она в этой области интегрируема.

Далее мы будем рассматривать только непрерывные функции, хотя двойной интеграл может существовать не только для непрерывных функций.

4.2. Геометрический смысл двойного интеграла

Р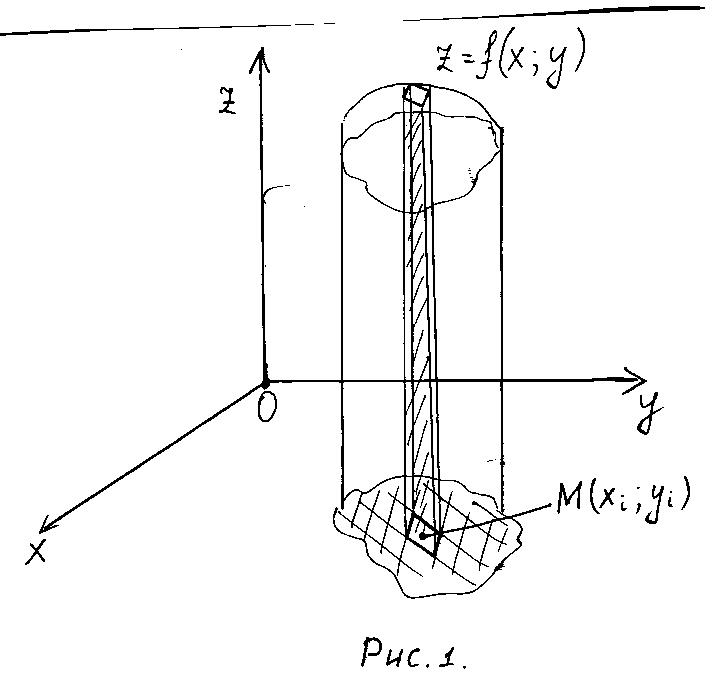ассмотрим задачу по определению объема цилиндрического тела. Пусть это тело ограничено сверху поверхностью≥0. Снизу замкнутой областьюплоскостис боков цилиндрической поверхностью, образующая которой параллельна осиOZ, а направляющей служит граница области(рис.1). Такое тело называется цилиндрическим. Найдем его объем V. Для этого разобьем область(проекция поверхностина плоскости) произвольным образом наобластей, площади которых равны. Рассмотрим цилиндрические столбцы с основаниями, ограниченные сверху кусками поверхности. На рис.1 один из них выделен. В своей совокупности они составляют тело. Обозначив объем столбика через, получим:.

Возьмем на каждой площади произвольную точкуи заменим каждый столбик прямым цилиндром с тем же основаниеми высотой. Объем этого цилиндра приближено равен объемуцилиндрического столбика, т.е.. Тогда получим. Это равенство тем точнее, чем больше числои чем меньше размеры элементарных областей. Естественно принять предел этой суммы при условии, что, аза объемцилиндрического тела, т.е.или записать эту сумму.

Итак, величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. В этом и состоит геометрический смысл двойного интеграла.