7.3 Вычисление объема тела

а) Вычисление объема тела по известным площадям параллельных сечений.

П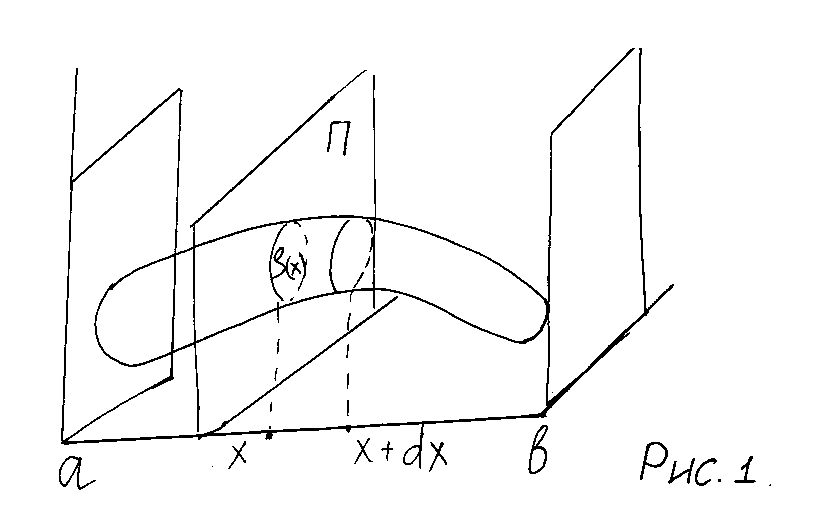усть требуется найти объем тела V при известной площади S сечений этого тела относительно плоскости, перпендикулярной некоторой оси, например, ох;. Применим метод 2.

Через произвольную точку проведем плоскость, перпендикулярную оси ох. Обозначим черезплощадь сечения тела этой плоскостью.считаем известной и изменяющейся непрерывно при изменении. Черезобозначим объем части тела, лежащие левее плоскости. Будем считать, что на отрезкевеличинаесть функция от, т.е.. Теперь найдем дифференциал функции. Он представляет собой слой тела, заключенного между параллельными плоскостями, пересекающими осьв точкахи, который можно приближено принять за цилиндр с основаниеми высотой(рис.1). поэтому дифференциал объема. Тогда для нахождения полного объема это соотношение надо проинтегрировать в пределах отдо.

- полученная формула называется формулой объема тела по площади параллельных сечений.

Пример: Найти объем эллипсоида. Если эллипсоид рассечен плоскостью, параллельной плоскостии на расстоянииот нееполучим эллипс (см. рис. 2).

.

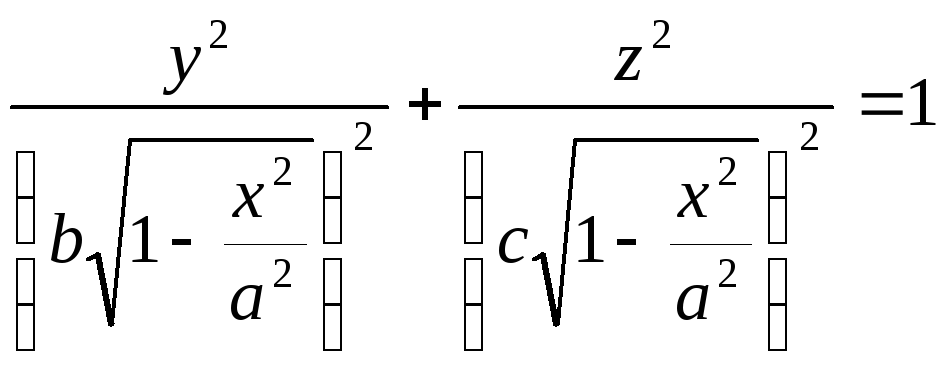
Площадь этого эллипса равна . Поэтому объем эллипсоида

б) Объем тела вращения

П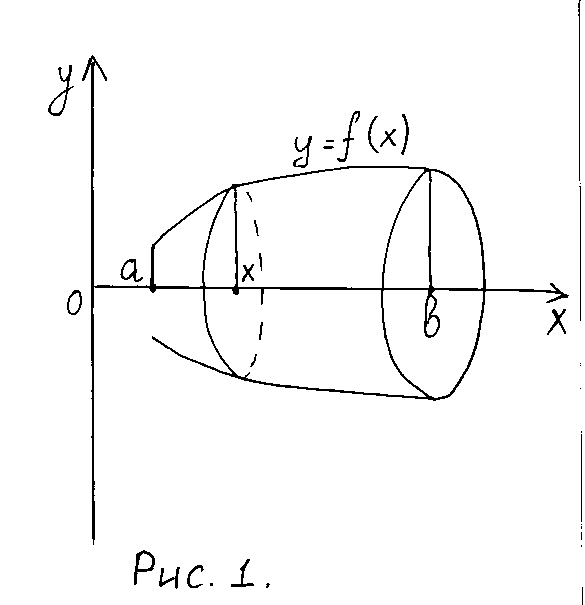усть вокруг осивращается криволинейная трапеция, ограниченная непрерывной линиейотрезкоми прямымии. Полученная от вращения фигура, называется телом вращения. Сечение этого тела - плоскостью, перпендикулярной оси, проведенной через произвольную точку, есть круг радиуса. Следовательно,. Поскольку- выражение для объема тела вращения вокруг оси. Если криволинейная трапеция ограничена графиком непрерывной функциии прямымипри условии, то для объема тела, образованного вращением этой трапеции относительно оси, по аналогии с полученным выше можно записать:

в) Вычисление координат центра тяжести плоской фигуры

П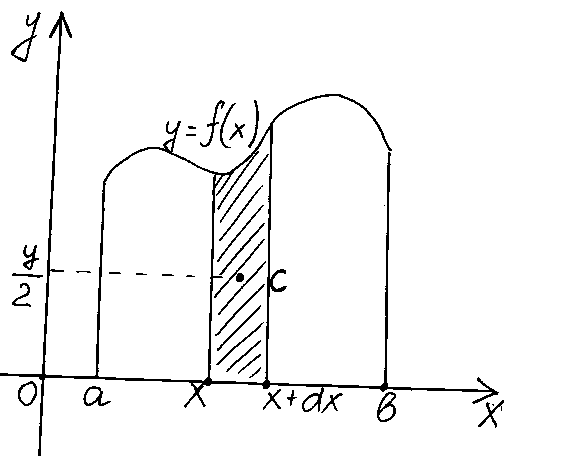усть дана материальная плоская фигура (пластина), ограниченная кривойи прямыми(рис. 2). Будем считать, что плотность пластиныесть величина. Тогда масса всей пластины, т.е.Выделим элементарный участок пластины в виде бесконечно малой узкой вертикальной полосы и будем считать его прямоугольником. Его масса равна. Центр тяжести прямоугольника лежит на пересечении диагоналей прямоугольника. Это точкастоит от осина расстоянии, а от осина расстоянии. Тогда для элементарных статистических моментов относительно осейиполучим следующие соотношения:и. Отсюда;. Если обозначим координаты центра тяжести плоской фигурыто получим, что;, т.е.илии.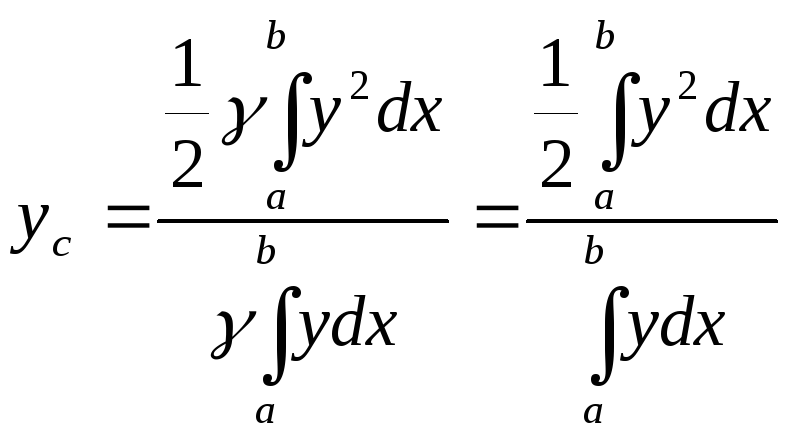

8. Приближенное вычисление определенного интеграла

Пусть требуется найти определенный интеграл от непрерывной функции. Если можно найти первообразнуюфункции, то интеграл находится по формуле Ньютона-Лейбница:

. Но поиск первообразной функции иногда весьма сложен, кроме того не для всякой функции первообразная выражается через элементарные функции. В этих и других случаях прибегают к приближенным формулам, с помощью которых интеграл находится с любой степенью сложности.

8.1. Формулы прямоугольников

П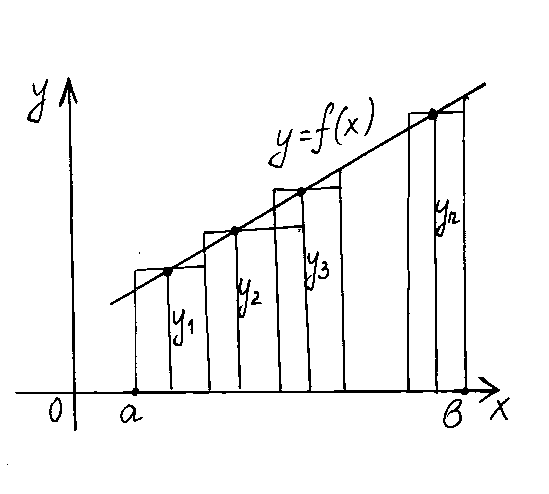усть на отрезкезадана непрерывная функция. Требуется вычислитьинтегралчисленно равный площади соответствующей трапеции. Разобьем основание этой трапеции, т.е. отрезокнаравных частей длиныс помощью точек. Можно записать, что. В середине каждого отрезка. Построим ординатуграфика функции. Приняв эту ординату за высоту, построим прямоугольник с площадью. Тогда сумма площадей всех прямоугольников даст площадь фигуры, представляющую собой приближенное значение искомого определенного интеграла: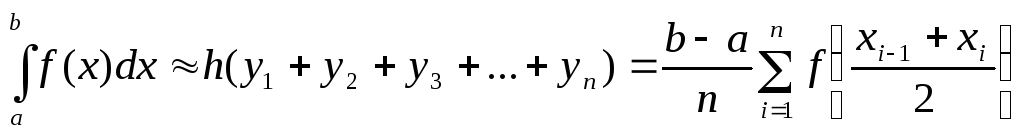. Эта формула и называется формулой прямоугольников. Абсолютная погрешность оценивается с помощью следующего соотношения, где- максимальное значениена отрезке.