Питання для самоконтролю

1. Судження: його структура (суб’єкт, предикат, зв’язка ). Судження і речення.

2. Основні види суджень.

3. Поділ суджень: за характером предиката, за якістю зв’язки, за обсягом суб’єкта, за модальністю.

4. Розподіленість термінів у простих атрибутивних судженнях.

5. Співвідношення між судженнями, логічний квадрат.

Бібліографічний список

Основна література (4), (9), (12)

Додаткова література (1)

Тема 4. Основні закони логіки. Умовиводи. Дедуктивні умовиводи

Мета: засвоїти що таке умовиводи, види умовиводів: безпосередні й опосередковані (дедуктивні, індуктивні, традуктивні). Закони формальної логіки. Правильність та істинність міркувань. Поняття силогізму; простий категоричний силогізм; структура простого категоричного силогізму (засновники: більший і менший, висновок, терміни: середній і крайній (більший і менший)). Модуси простого категоричного силогізму (загальні поняття). Складні, скорочені і складно-скорочені категоричні силогізми (полісилогізм, ентимема, сорит), езпосередні умовиводи (перетворення, обернення, протиставлення предикату).

План вивчення теми

1. Що таке умовиводи, види умовиводів: безпосередні й опосередковані (дедуктивні, індуктивні, традуктивні).

2. Правильність та істинність міркувань. Поняття силогізму; простий категоричний силогізм; структура простого категоричного силогізму (засновники: більший і менший, висновок, терміни: середній і крайній (більший і менший)).

3. Модуси простого категоричного силогізму (загальні поняття). Складні, скорочені і складно-скорочені категоричні силогізми (полісилогізм, ентимема, сорит, епіхейрема).

4. Безпосередні умовиводи (перетворення, обернення, протиставлення предикату).

5. Силогізм зі складаними і простими засновниками (розподілово-категоричний, умовно-категоричний, умовно-розділовий).

Методичні рекомендації до самостійної роботи

Закони логіки використовуються при розв’язанні складних логічних задач у кібернетиці, теорії релейно-контактних схем, у роботі електронно-обчислювальних машин, автоматичних пристроїв, математичній лінгвістиці тощо.

Закон тотожності виражає тотожність думки самій собі. Цей закон дозволяє досягти визначеності мислення. Визначеність думки – істотна властивість правильного мислення. Думка повинна зберігати чітко визначений зміст, скільки б разів вона не повторювалася.

Закон тотожності формулюється так: кожна думка має бути чіткою за обсягом, ясною за змістом і залишатися незмінною в ході одного й того ж міркування.

Із сутності закону випливає важлива вимога: не можна різні думки приймати за тотожні. Цей закон спрямований безпосередньо проти нечітких, неясних, розпливчастих думок, а опосередковано – проти їх двозначності та багатозначності.

Закон тотожності записується таким чином: „Р є Р” (або Р = Р), де Р означає будь-яку думку. Формула читається „Р тотожно Р”. В символічній логіці цей закон виражається формулою РР, де Р – якесь висловлювання. Читається: „якщо Р, то Р” або ж: 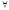х (Р(х) Р(х)), де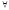– квантор загальності, що заміняє слова „будь-який”, „жоден”. Читається так: „для всякого х істинно, що якщо х має Р, то х має цю властивість”, „Р тоді і тільки тоді, коли Р”.

Вперше закон тотожності сформулював Арістотель. Він писав, що неможливо що-небудь мислити, якщо не мислять щось одне. Арістотель не дав закону своєї назви. Вона з'явилося в логіці пізніше. Сам же закон в різні епохи, в різних народів отримував неоднозначне тлумачення і досить різні формулювання.

Закон тотожності виявляє „свою дію” у процесі використання вже існуючих понять. Якби в них не було визначеності, якби вони кожного разу змінювали свій зміст і свій обсяг, то ми не могли б їх застосовувати. Так, знаючи точне визначення поняття „товар”, ми можемо чітко, однозначно відповісти, у якому випадку та або інша річ, що задовольняє вимогам людини, є товаром.

Якби поняття не були визначеними за своїм змістом й обсягом, то ми не змогли б виділити їхні види і роди, встановити стосунки між ними, робити над ними логічні операції – визначення, розподіл, узагальнення та обмеження.

Закон тотожності застосовується також і до аналізу суджень. Визначеність понять, з яких вони утворюються, служить найважливішою передумовою їхньої визначеності. Але і цим дієвість закону тотожності не вичерпується. Адже найбільш глибока сутність суджень виявляється у відтворюваних ними зв'язках і відносинах дійсності. Якщо ці зв’язки і відносини визначені, то і судження буде вірно „відображати” їх. Воно буде визначеним.

Найбільш однозначно закон тотожності виявляється в судженнях типу: „Сонце є сонце” або „Війна є війна”... і т.п. У них безпосередньо розкривається тотожність предмета із самим собою. Такі судження часто мають місце у практиці мислення. Різновидом суджень, що виражають об'єктивну тотожність, є судження типу: „Негативний результат – теж результат” та ін.

Закон тотожності поширюється і на значну кількість умовиводів. Так, простий категоричний силогізм можливий, зокрема, тому що середній термін, що зв'язує більшу і меншу посилки, зберігає в них той самий зміст. А більший і менший терміни не тільки зберігають свій зміст у посилках і висновках, але якщо вони не розподіляються у посилках, то не можуть бути розподілені і в висновку. В іншому випадку, силогізм виявляється неправильним. Нарешті, у доведенні, якщо воно теж є вірним, закон тотожності проявляється у тому, що і теза, і засади зберігають своє .значення і зміст протягом усієї даної логічної процедури. Без цього доведення не відбулося б, або було б неправильним.

З цього короткого огляду видно, що закон тотожності універсальний у значенні охоплення усіх без винятку форм мислення, будь-якої думки взагалі.

Із закону тотожності випливають певні вимоги. Це логічні норми, установки, приписи або правила, що формулюються самими людьми на основі закону, і яких необхідно дотримуватись, щоб мислення було правильним, таким, що веде до істини. Їх можна звести до наступних:

а) кожне поняття, судження і т.д. повинне вживатися в тому самому, визначеному змісті і залишатися незмінним в процесі всього мислення;

б) закон тотожності вимагає досягнення визначеності думки у термінах (іменах). Це означає, що кожний термін (ім’я), який використовується у засновках, має бути точно визначеним. Наприклад, стверджуючи, що „А є В”, необхідно встановити тотожність „А” і „В”. Так, визначаючи трикутник А як геометричну фігуру В, ми припускаємося помилки, оскільки судження В має загальний зміст. Правильним визначенням буде наступне: трикутник – це геометрична фігура на площині, що обмежена трьома прямими, що перетинаються, і внутрішні кути якого дорівнюють 180;

в) закон тотожності вимагає розрізнювати формальну і змістовну тотожність;

г) закон тотожності характеризується комунікативним аспектом. В процесі спілкування необхідно враховувати тотожність і відмінність між словами. Мається на увазі синонімія, омонімія, полісемія.

Вимагаючи визначеності, однозначності думки, закон тотожності, у той же час, спрямований проти будь-якої нечіткості, неточності, розмитості наших думок, понять і таке інше. У тих випадках, коли вимоги закону тотожності порушуються, виникають численні логічні помилки. Вони називаються по-різному: „амфіболія” (двозначність, тобто вживання того самого слова-аноніма одночасно у різних смислах), „змішання понять”, „плутанина в поняттях”, „підміна одного поняття іншим”, „підміна тези” і таке інше.

Дуже важливо дотримуватися вимог закону тотожності у дискусіях і суперечках. Щоб дискусія не була безпредметною, необхідно завжди точно визначати предмет дискусії і точно з'ясовувати зміст ключових понять у ній.

Закон несуперечностіУперше цей закон сформулював Арістотель. Він писав, що „невозможно, чтобы одно и то же в одно и то же время было и не было присуще одному и тому же, в одном и том же отношении”. В іншому місці: „Невозможно что-либо вместе утверждать и отрицать”.

Чому ж цей закон отримав назву несуперечності? Перш за все тому, що цим законом описується логічне протиріччя. Що таке логічне протиріччя? Очевидно, що це два несумісних, взаємовиключаючих одне одного висловлювання про що-небудь. Однак далеко не завжди взаємовиключаючі висловлення виявляються логічним протиріччям. Розглянемо, як приклад, наступні пари міркувань. Наприклад: „Ніч довга” – „День короткий”. Тут ми маємо два протилежних висловлювання. Однак вони стосуються різних явищ. Такі два висловлення можуть бути одночасно істинними. Логічного протиріччя тут немає, є лише відображення протилежних властивостей, які характеризують день і ніч.

А якщо ми висловимо дві протилежні думки про один і той самий предмет? Чи можуть вони бути одночасно істинними, тобто, чи не утворять вони логічне протиріччя? Ні, але за умови, якщо предмет розглядається в різний час. Наприклад: „Жовтневий день короткий” – „Червневий день довгий”. Чи можуть бути одночасно істинними протилежні висловлювання про один і той самий предмет, узяті в один і той же час? Так, але при одній умові: якщо він розглядається у різних відношеннях. Наприклад: „Жовтневий день короткий у порівнянні з червневим” – „Жовтневий день довгий у порівнянні із січневим”. Розглянемо, нарешті, останній випадок. Чи можуть бути одночасно істинними два протилежних судження про один і той самий предмет, які розглядаються в той же самий час і у тому самому відношенні? Ні. Жовтневий день у порівнянні з червневим, не може бути одночасно і довгим, і коротким Якщо ми будемо міркувати так, то допустимо логічне протиріччя.

Логічне протиріччя – це такий характер мислення, коли висловлюються два взаємовиключаючих судження про один і той самий предмет, який розглядається в той же самий час і в тому самому відношенні. Що ж характерно для логічного протиріччя? Яка у ньому прихована закономірність? Як ми могли переконатися, на відміну від інших висловлювань, два таких висловлювання не можуть бути одночасно істинними. Сфера закону несуперечності широка. Цей закон є, насамперед, узагальненням практики оперування судженнями. У ньому відображається закономірне відношення між двома судженнями – стверджувальним і заперечним, відношення несумісності за їх істинністю: якщо одне з них істинно, то інше неодмінно хибне. Оскільки судження поділяються на стверджувальні і заперечні, а вони, у свою чергу, на істинні і хибні, то цим пояснюється універсальний характер закону несуперечності. Природно, що оскільки з простих суджень утворюються складні, то закон протиріччя діє і тоді, коли вони знаходяться у відношенні заперечення.

Цей закон описує також відношення між поняттями, зокрема, відношення несумісності. Так, якщо ліс „хвойний”, то він не може бути „листяним” (відношення супідрядності); якщо людина „щедра”, то вона не може бути „скупою” (відношення протилежності). Звичайно, все це виявляється у процесі функціонування понять.

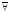
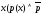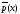Закон несуперечності виражається формулою „Р не є не-Р”, зміст якої полягає в тому, що не можуть бути одночасно істинними судження „Р” і його заперечення „не-Р”. Символічно закон виражається за допомогою квантора спільності (х)), де – заперечення усієї формули, – заперечення Р(х), тобто (не-Р(х)). Читається: „для всякого Р(х) має місце, що Р(х) і його заперечення не можуть бути одночасно істинними”.

Закон несуперечності іноді називають законом непротиріччя, оскільки він заперечує протиріччя суджень і умовиводів, вказує на помилку і, тим самим, вимагає несуперечності. В історії розвитку філософії і логіки закон несуперечності відіграв „видатну” роль. Чи можна просте механічне переміщення описати несуперечливо? Саме так була сформульована проблема давньогрецьким філософом Зеноном в апорії „Стріла”. Її зміст полягає у тому, що рух неможливий при допущенні переривчастості простору. На думку Зенона, траєкторію стріли, що летить, можна представити як сукупність „місць” чи крапок, які займає стріла у послідовні моменти часу. Зенон ототожнював предмет і його місце: стріла стоїть, тому що вона всякий раз співпадає зі своїм місцем, а співпадає зі своїм місцем – отже, стоїть у ньому.

Цікаві докази і міркування Арістотель, який одним із перших проаналізував апорію Зенона „Стріла” (Аристотель. Соч. В 4-х Т. – Т.3. – М., 1981. – С. 179 – 181).

На думку деяких дослідників, апорії Зенона послужили логічною основою розвитку механіки (Библер В.С. Генезис понятия „движение” (Категории механики) // Анализ развивающегося понятия. – М., 1967. – С. 119 – 193).

Відомий логік О.А. Івін, характеризуючи цю проблему, пише: „Рух внутрішньо суперечливий і вимагає для свого опису об'єктів типу рухоме тіло, що знаходиться в даному місці, і рухоме тіло, що не знаходиться в даному місці”.

Оскільки суперечливий не лише механічний рух, але і всяка зміна зовні, будь-яке описуване явище в динаміці повинно бути – при такому підході – внутрішньо суперечливим. Зрозуміло, цей підхід являє собою „непорозуміння” (Ивин А.А. Логика. Учеб. пособие. – М., 1977. – С. 15).

Як бачимо, логіка закону несуперечності і його „застосування” на практиці у різних авторів і донині викликає неадекватну оцінку. Корисно проаналізувати міркування Арістотель, який, зокрема, писав: „Третье – (рассуждение Зенона. – авторы), о котором только что было упомянуто, состоит в том, что летящая стрела стоит неподвижно; это вытекает из предположения, что время слагается из [отдельных] „теперь”; если это не признать, силлогизма не получится” (Аристотель. Соч. В 4-х Т. – Т.3. – С. 200).

Закон несуперечності містить декілька вимог до висловлювання думки:

а) забороняє використання протилежних (взаємовиключаючих) суджень в структурі одного міркування;

б) визначає критерій логічності міркування як несуперечність;

в) спонукає відшукувати істинні кваліфікації суджень, що використовуються у міркуваннях;

г) вимагає виявляти неприховані і приховані протиріччя у структурі міркування;

д) зобов’язує розрізняти реальні і уявні протиріччя.

Слід зазначити, що використання закону протиріччя приводить дослідника до питання про „природу” і форму протиріччя. Це досить складна проблема. Традиційно виділяють такі форми протиріччя.

Діалектичне протиріччя. Навколишня (соціальна і природна) дійсність мінлива і рухома, дійсність постійно і безперервно змінюється. Якщо уважно розглядати будь-який матеріальний процес, то в ньому легко виявити протилежні, виключаючі одна одну сторони існування властивостей, зв’язків, відношень. Ці протиріччя існують об’єктивно, в самій дійсності і знаходять своє віддзеркалення, відображення у людських думках, тому діалектичне протиріччя (якщо брати до уваги розвиток знань) є протиріччям знання, яке розвивається. Будь-яке об’єктивне протиріччя на рівні теоретичного мислення необхідно відобразити максимально точно „в логічно несуперечливій формі”, щоб за можливостями не ототожнювати суб’єктивні і об’єктивні протиріччя.

Проблема об’єктивного протиріччя, так чи інакше, приводить до питання про співвідношення діалектичної і формальної логіки і, зокрема, про застосування основних форм мислення (поняття, судження і умовивід) в діалектичній логіці.

Ми вважаємо, що мислення людини (незалежно від того, усвідомлює вона це чи ні) не обмежується тільки цими трьома формами мислення. Воно значно ширше. Зокрема, людина використовує філософські категорії. Аналіз філософських категорій виходить за межі формальної логіки.

Коротко охарактеризуємо особливості понять і суджень як форм мислення.

Логічне протиріччя є відношенням взаємовиключаючих суджень, які розглядаються в одному контексті. Кожне, будь-яке судження тотожне самому собі і не змінюється у структурі даного міркування.

Протиріччя-парадокс – особливий вид протиріччя. Відомий парадокс Бертрана Рассела про цирульника, який голить тих чоловіків, які не голяться самі (самостійно). У підсумку, на питання, хто голить цирульника – немає відповіді. Якщо він голить сам себе, то його не може голити цирульник (а він і є цирульником) і, навпаки, якщо його голить цирульник, то він не може голити сам себе. В жартівливій формі тут закладено протиріччя-парадокс, який привів до кризи теорії множин (фундаментального розділу математики), оскільки Б. Рассел мав на увазі різні множини і підмножини. Парадокси вказують на те, що є факти, які суперечать існуючим науковим теоріям.

Закон виключеного третього формулюється так: із двох суджень (висловлювань), в одному з яких стверджується те, що заперечується в іншому, – одне неодмінно істинно. Наприклад: „Самара впадає у Дніпро”, „Самара не впадає у Дніпро”. Одне із суджень істинне, а інше – хибне.

Символічно закон виключеного третього записується формулою: „Р або не-Р”. Читається формула так: „Р або (невірно, що Р)”.

Назва закону виражає його зміст: із двох суперечних одне одному висловлювань одне – істинне. Третьої можливості немає. Зазначений закон був відомий ще Арістотелю. Але давньогрецький філософ висловив сумнів в універсальній „дії” закону виключеного третього. „...Невозможно, – писав Арістотель, – чтобы одно и то же в то же время было и не было присуще одному и тому же в одном и том же отношении (и все другое, что мы могли бы еще уточнить, пусть будет уточнено во избежание словесных забруднений) – это, конечно, самое достоверное из всех начал”.

Варто мати на увазі, що закон виключеного третього стосується тільки осмислених висловлювань. Проте, аналіз закону виключеного третього голландським математиком Л. Брауером і російським математиком М.О.Васильєвим привів до створення нового напрямку у логіці – інтуїтивістської логіки, у якій даний закон не приймається і відкидаються всі способи і міркування, що пов'язані з ним.

Щоб зрозуміти зміст закону, наведемо дві пари несумісних висловлювань.

1) „Байкал глибокий” – „Байкал мілкий”;

2) „Байкал глибокий” – „Байкал неглибокий”.

У першій парі суджень предикатами виступають протилежні поняття („глибокий” і „мілкий”), а у другій – суперечні поняття („глибокий” – „неглибокий”). Між ними є не тільки подібність, але і відмінність. Протилежні поняття заперечують один одного, але не вичерпують обсягу родового. Чи можуть два висловлювання з протилежними предикатами бути одночасно істинними? Ні. Про це говорить закон несуперечності. Але чи можуть вони бути одночасно хибними? Так, тому що не вичерпують всі можливі варіанти. Можна сказати, що „Байкал середньої глибини”. Закон виключеного третього тут не діє.

Що ж стосується суперечних понять („глибокий” – „неглибокий”), то вони не тільки заперечують один одного, але й вичерпують обсяг родового поняття. Виникають ті ж самі питання. Чи можуть обидва судження з подібними предикатами бути одночасно істинними? Ні. В даному випадку справедливий закон несуперечності. А чи можуть вони бути одночасно хибними? На відміну від першої пари, вони не можуть бути одночасно хибними. Адже третього тут не існує, тому що озеро або глибоке, або неглибоке. Одне із них неодмінно істинне.

Неважко зрозуміти, яка сфера дії цього закону. Вона теж досить широка. Як і закон несуперечності, закон виключеного третього – це результат узагальнення практики застосування суджень. Але якщо в законі несуперечності відображаються відносини за істинністю, то в законі виключеного третього – за хибністю. (Він діє у відносинах між суперечними (контрадикторними) судженнями (А-О, Е-І)). Але цей закон не спрацьовує у відносинах між протилежними (контрарними) судженнями (А-Е), хоча закон несуперечності діє і тут: вони не можуть бути разом істинними, але можуть бути одночасно хибними. Сфера закону виключеного третього виявляється й у складних судженнях (наприклад, у строгій диз'юнкції, коли складові судження взаємно виключають один одного, а, отже, не можуть бути разом не тільки істинними, але і помилковими).

Закон виключеного третього діє також в умовиводах і доказах.

Наприклад, він лежить в основі безпосередніх умовиводів через перетворення суджень у логічному квадраті. Встановлюючи хибність якої-небудь тези, ми тим самим доводимо істинність суперечній їй тези, оскільки обоє вони не можуть бути разом хибними. Враховуючи цей закон можна сформулювати певні вимоги до мислення. Щоб зрозуміти принциповий зміст цього закону, згадаємо історію з бурідановим ослом. Як говорить легенда, він помер від голоду, тому що так і не зміг вибрати одну з однакових (зовсім однакових) оберемків сіна. Перед людиною теж нерідко постає дилема, але вже інша: вибирати не з однакових, а із взаємозаперечувальних висловлювань. Закон виключеного третього саме і висуває вимогу вибору – одного з двох – за принципом “або”, “tertium nin datur” (третього не дано). Він означає, що при розв'язанні альтернативного питання, не можна ухилятися від однозначної відповіді; не можна шукати щось проміжне, середнє, третє. З такого роду альтернативами людина зустрічається досить часто. Ще в Стародавньому Римі народився крилатий вислів: “Aut Caesar, aut nihil” (буквально “Або Цезар, або ніщо”), який іноді вживають в узагальненому розумінні: “Все або ніщо”.

Закон виключеного третього містить у собі такі вимоги:

а) формулює альтернативність А і не-А і вимагає зробити вибір між ними за істинними ознаками;

б) забороняє вибирати замість альтернативи ще які-небудь судження (наприклад, або людина смертна, або безсмертна);

в) встановлює відношення контрарності (протилежності) між альтернативними поняттями, судженнями таким чином, що кожне з них є запереченням іншого;

г) містить вимогу до логічного мислення, згідно якої протилежне істині є хибність.

Закон достатньої підстави вимагає, щоб ніщо не приймалося просто так на віру. У кожному висловлюванні варто вказувати підстави, завдяки яким воно вважається істинним. Закон: “всяка думка повинна мати достатню підставу” виражає обов'язковість структури думки, що приводить до істини. Можна сказати, що у своїй діяльності люди керуються наступним принципом: якщо ти хочеш, щоб висловлену тобою думка визнали інші, постарайся обґрунтувати її.

Закон достатньої підстави теж містить ряд вимог:

а) всі засновки мислення (умовиводи, доведення, висновки) мають бути обґрунтованими;

б) обґрунтованою вважається будь-яка істинна характеристика судження (хибне судження, імовірне судження);

в) в обґрунтуванні суджень необхідно розрізняти логічне обґрунтування і фактичне обґрунтування.

Умовивід – це форма мислення, в якій з одного або кількох істинних суджень-засновків на основі певних правил виводу отримують нове судження-висновок, який логічно випливає із змісту вихідних суджень. Взагалі умовиводи за спрямованістю процесу мислення, залежно від того, як рухаються знання, – від більш загального до менш загального, від одиничного до часткового чи й до загального, від знань певного ступеня загальності до знань такого ж ступеня загальності – поділяються на дедуктивні, індуктивні, традуктивні, або умовиводи за аналогією (аналогія).

Безпосередній – умовивід, до складу якого входить лише один засновок. Це вид дедуктивних умовиводів, в яких з одного судження (засновку), за певними правилами, виводять нове судження (висновок). Оскільки засновок безпосереднього умовиводу виражається судженням, то цей вид умовиводу здійснюється у формі перебудови судження.

За способом утворення висновків, тобто за способом перебудови судження-засновку, розрізняють три види безпосередніх умовиводів: перетворення, обернення, протиставлення предикату, протиставлення суб’єктові, умовиводи за логічним квадратом і на основі одиничного судження.

Обернення – це перебудова судження, внаслідок якої суб’єкт і предикат міняються місцями, зв’язка залишається без зміни, квантор перед новим суб’єктом визначається за правилом: якщо предикат в засновках нерозподілений, то він не може бути розподіленим в якості суб’єкта у висновку.

Основою для обернення є, зокрема, та обставина, що в судженні містяться знання про предмети, які мисляться як у суб’єкті, так і в предикаті. Внаслідок обернення змінюється предмет думки. Наприклад:

Всі матеріалісти – філософи.

Отже, деякі філософи – матеріалісти.

В обох судженнях мислиться тільки те, що передається на схемі заштрихованою її частиною. У першому судженні обсяг поняття „матеріалісти” (менший круг на схемі) ототожнюється з частиною обсягу поняття „філософи” (на схемі – та частина більшого кругу, яка закрита меншим). А в другому судженні (висновку) – навпаки.

Здійснюючи обернення, необхідно дотримуватися вимоги рівності обсягів термінів: обсяги термінів висновку повинні дорівнювати обсягам відповідних термінів засновку. Правда, сама структура судження не завжди чітко виражає характер обсягу термінів. Це стосується, передусім, предикатів стверджувальних суджень.

Традиційно розрізняють два види обернення: просте, або чисте, і обернення з обмеженням. Проте такий поділ має штучний характер. Прості обернення утворюються тоді, коли і S і Р вихідного судження або розподілені, або нерозподілені. Обернення з обмеженням можна зробити тоді, коли у вихідному судженні суб’єкт є розподіленим, предикат – нерозподіленим, або навпаки. Наведемо приклад простого обернення: „Деякі студенти – спортсмени. Деякі спортсмени – студенти”. Прикладом обернення з обмеженням може бути: „Всі гітаристи – музиканти. Деякі музиканти – гітаристи”.

Розглянемо, як здійснюється обернення суджень, різних за кількістю і якістю (А, Е, І, О).

1. Загальностверджувальне судження – (А). (Всі S є Р / Деякі Р є S). Наприклад: Всі люди є смертними істотами (А). Отже, деякі смертні істоти є людьми (І). Інший приклад: Всі квадрати є ромбами з прямими кутами (А). Отже, всі ромби з прямими кутами є квадратами (А).

Деякі загальностверджувальні судження перебудовуються при оберненні на загальнозаперечні.

2. Загальнозаперечне судження – Е. (Жодне S не є Р / Жодне Р не є S) – обертається на загальнозаперечне. Наприклад:

Жоден патріот не відмовляється від культури свого народу (Е).

Отже, жоден з тих, хто відмовляється від культури свого народу,

не є патріотом (Е).

3. Частковостверджувальне судження – (І). (Деякі S є Р / Деякі Р є S) при оберненні, як правило, перебудовується на частковостверджувальне.

Наприклад: Деякі вчені – митці (І)

Отже, деякі митці – вчені (І).

Інколи частковостверджувальні судження перебудовуються при оберненні на загальностверджувальні. Це стосується виділяючих суджень.

Наприклад: Деякі люди, і тільки люди, мають високу мораль.

Отже, всі, хто має високу мораль – люди.

4. Частковозаперечне судження – (О) операції обернення практично не підлягають, бо при оберненні вони дають невизначені знання.

Наприклад: Деякі птахи не хижаки (О).

Отже, жоден хижак не належить до птахів-нехижаків (Е).

Перетворення – це перебудова судження, внаслідок якої з вихідного судження (засновку) виводиться рівнозначне нове судження (висновок), але протилежної якості: стверджувальне судження перетворюється на заперечне, а заперечне – на стверджувальне. Перетворення – це такий умовивід, який дозволяє отримати нові знання про суб’єкт через визначення його відношення до доповнення предиката. Перетворення здійснюється шляхом подвійного заперечення: частку „не” ставимо перед зв’язкою та предикатом.

Наприклад: Всі S є Р

Всі S не є не-Р

Наприклад: Всі веселки є чудовим явищем природи.

Всі веселки не є не чудовим явищем природи.

Якщо перетворюються загальнозаперечні або частковозаперечні судження, то слід запам’ятати, що заперечуюча зв’язка перетворюється на стверджувальну.

Жодне S не є Р

Жодне S не є не-Р

Жодне S є не-Р

Наприклад: Жодний кит не є рибою.

Всі кити є не риби.

Перетворенню підлягають всі чотири типи суджень А, І, Е, О за такими схемами:

А	Всі S є Р. Отже, жодне S не є не-Р.	Всі метали електропровідні. Отже, жоден метал не є не електропровідним.
Е	Жодне S не є Р. Отже, всі S є не-Р.	Жоден патріот не є зрадником. Отже, кожен патріот є незрадником.
І	Деякі S є Р. Отже, деякі S не є не-Р.	Деякі числа прості. Отже, деякі числа не є непрості.
О	Деякі S не є Р. Отже, деякі S є не-Р.	Деякі числа не є прості. Отже, деякі числа є непрості.

Здійснюючи перетворення судження, необхідно змінити його якість, залишивши без змін кількість. Замінивши зв’язку “є” на “не є”, домагаємося перетворення стверджувального судження на заперечне. Але одержане судження виявляється нерівнозначним вихідному. Щоб нейтралізувати вказаний вплив частки “не”, треба ввести ще одну аналогічну частку, приєднавши її до імені, яким позначається предикат висновку. Внаслідок такої процедури предикатом висновку стає поняття, суперечне предикатові засновку. А замінивши зв’язку “не є” заперечного судження-засновку на “є”, домагаємося перетворення заперечного судження на стверджувальне. Але при цьому знову змінюється зміст вихідного судження. Вихід тут один: до імені, яким позначається предикат висновку, слід додати частку “не”, тобто знов-таки предикат засновку замінюється у висновку на суперечне йому поняття.

Під збереженням кількості судження мають на увазі, що загальностверджувальне судження перетворюється на загальнозаперечне (і навпаки), а частковостверджувальне – на частковозаперечне (і навпаки). Безпосередньо ж це виявляється в збереженні тих самих кванторів (чи відповідних кванторних слів).

Результат перетворення можна знову перетворити на вихідне судження. Ця закономірність виражається таким правилом: подвійне заперечення будь-чого рівносильне ствердженню того ж самого.

Наприклад: Київ – столиця України.

Отже, Київ не є нестолицею України.

Отже, Київ є не нестолицею України

(що рівнозначно судженню “Київ – столиця України”).

Протиставлення – перебудова судження, в ході якої одночасно здійснюються і перетворення, і обертання в тій чи іншій послідовності.

Якщо судження спочатку перетворюється, а потім обертається, то такий умовивід називається протиставленням предикатові. А якщо судження спочатку обертається, а потім перетворюється, то ми маємо справу з протиставленням суб’єктові.

При протиставленні предикатові суб’єкт вихідного судження стає предикатом висновку, а суб’єктом висновку виступає поняття, суперечне предикатові вихідного судження (засновку).

Коротко зміст цієї логічної операції можна виразити так:

1. замість Р беремо не-Р;

2. міняємо місцями S і не-Р;

3. зв’язку міняємо не протилежну.

Отже, щоб здійснити протиставлення предикату, треба спочатку виконати перетворення судження, а потім – обернення.

Наприклад:

1. Будь-яка наукова теорія об’єктивно відображає дійсність.

2. Будь-яка наукова теорія є такою, що об’єктивно відображає дійсність.

3. Будь-яка наукова теорія не є такою, що не об’єктивно відображає дійсність.

Висновок:

4. Будь-яка наукова теорія, що не об’єктивно відображає дійсність, не є такою.

Розглянемо, як здійснюється протиставлення предикатові в судженнях типу А, Е, І, О.

1) Загальностверджувальне судження (А) перебудовується за схемою “Всі S є Р. Отже, жодне не-Р не є S”.

Наприклад: Всі квадрати паралелограми (А).

Отже, жоден непаралелограм не є квадратом (Е).

Здійснимо цю логічну операцію шляхом послідовного застосування перетворення і обернення:

Всі квадрати – паралелограми (А).

Отже, жоден квадрат не є непаралелограмом (Е).

Отже, жоден непаралелограм не є квадратом (Е).

Тут обсяг поняття “квадрат” несумісний з обсягом поняття “непаралелограм”. Розглянемо це за допомогою схеми 2. Загальностверджувальне судження:

Схема 2. Загальностверджувальне судження

2. Загальнозаперечне судження (Е) перебудовується за схемою “Жодне S не є Р. Отже, деякі не-Р є S”.

Наприклад: Жодне просте число не ділиться на чотири (Е).

Отже, принаймні деякі числа, що не діляться на чотири, є простими (І).

Послідовно застосувавши перетворення і обернення, одержимо:

Жодне просте число не ділиться на чотири (Е).

Отже, кожне просте число є тим, що не ділиться на чотири (А).

Отже, принаймні деякі числа, які не діляться на чотири, є простими (І).

3. Перебудова частковостверджувального судження (І) у формі протиставлення предикатові дає бідне, невизначене знання, тому до неї практично не вдаються.

4. Частковозаперечне судження перебудовується у формі протиставлення предикатові за схемою “Деякі S не є Р. Отже, деякі не-Р є S”.

Наприклад: Деякі ссавці не є хижаками (О).

Отже, деякі нехижаки є ссавцями (І).

Можна дійти висновку, що при протиставленні предикатові якість усіх суджень змінюється.

Третій вид умовиводу цікавий тим, що він будується як комбінація перших двох: перетворення + обернення. Ну, а якщо ми результат протиставлення предикату знову перетворимо? В такому випадку ми отримаємо вид безпосереднього умовиводу, який зазвичай не аналізується в літературі з логіки, але який є цілком реальним. Таким чином проводимо: перетворення + обернення + перетворення. Що ж ми отримаємо? Розглянемо на прикладі загальностверджувального судження.

Всі S є Р. Перетворюємо. Жодне S не є не-Р. Проводимо обернення. Жодне не-Р не є S. Перетворюємо. Всі не-Р є не-S. Що ми отримали?

Ми отримали загальностверджувальне судження про відношення доповнення до предикату до доповнення до суб’єкту. Змістовний приклад:

Всі веселки – чудові.

Все, що нечудово, є не-веселкою.

Зрозуміло, що ми отримали вид безпосереднього умовиводу, якому ще немає певної назви. Але важливо підкреслити, що і традиційна логіка не є закритою системою і зовсім не виключає досліджень і експериментів.

При протиставленні суб’єктові предикат вихідного судження стає суб’єктом висновку, а предикатом висновку береться поняття, суперечне суб’єктові засновку. При цьому якість судження завжди змінюється.

Розглянемо, як здійснюється протиставлення суб’єктові в судженнях, різних за кількістю і якістю (А, Е, І, О).

Протиставлення суб’єктові відбувається за різними схемами в судженнях різного типу (А, Е, І, О).

1. Загальностверджувальне – “Всі S є Р. Отже, деякі (жоден) Р не є не-S”.

Наприклад: Всі квадрати є ромбами.

Отже, деякі ромби не є неквадратами.

2) Загальнозаперечне – “Жоден S не є Р. Отже, всі Р є не-S”.

Наприклад: Жоден ромб не є трикутником.

Отже, всі трикутники є неромбами.

3) Частковостверджувальне – “Деякі S є Р. Отже, деякі (жоден) Р не є не-S”.

Наприклад: Деякі студенти – спортсмени.

Отже, деякі спортсмени не є нестудентами.

4) Частковозаперечне судження, як правило, не піддається перебудові за схемою протиставлення суб’єктові, оскільки така операція малоефективна.

До безпосередніх часто відносять і деякі інші різновиди умовиводів, зокрема, контрапозицію просту (її формула: (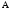)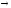(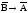)) та ті умовиводи, в основі яких лежить характервідношень між судженнями за “логічним квадратом”.

Безпосередні умовиводи мають певне пізнавальне значення, а їх осмислення підвищує логічну культуру людини. Вони дають можливість одержати нову інформацію; виявити знання, які містяться в судженні неявно; уточнити співвідношення обсягів суб’єкта і предиката; чітко усвідомити, яка інформація є в судженні, а якої немає; тонко охопити майже невловимі нюанси думок.

Категоричним силогізмом називається такий опосередкований дедуктивний умовивід, що складається з двох засновків (посилок) і висновку, які є категоричними судженнями. До складу простого категоричного силогізму входять: більша посилка, менша посилка і висновок.

Поняття, які входять до складу силогізму, називають його термінами. Оскільки до складу простого категоричного силогізму входять три простих судження, то звідси випливає висновок, що цей силогізм складається із шістьох термінів. Проте при ближчому ознайомленні з ним виявляється, що до його складу входять лише терміни, кожен з яких двічі повторюється. Отже, кожний простий категоричний силогізм має три терміни.

Наприклад: Всі люди (М) смертні (Р).

Сократ (S) – людина (М).

Отже, Сократ (S) – смертний (Р),

де: S – Сократ; Р – смертний; М – люди; “всі” – квантор загальності.

Неважко помітити, що в засновках є всі три терміни, які фігурують у силогізмі, а один термін навіть двічі повторюється (у нашому прикладі – “люди”, “людина”).

Термін, який повторюється в засновках і пов’язує їх між собою, але відсутній у висновку, називається середнім, а два інших терміни – крайніми.

Ширший за обсягом (родовий) крайній термін називають більшим (він виконує у висновку роль предиката), а вужчий за обсягом крайній термін – меншим (він виконує у висновку роль суб’єкта).

Засновок, до складу якого входить більший термін, називають більшим, а засновок, до складу якого входить менший термін – меншим.

Беручи до уваги саме таку будову простого категоричного силогізму та роль у ньому середнього терміна, його можна визначати і як такий, який є умовиводом про відношення двох термінів на підставі їх відношення до третього терміна.

Отже, запам’ятаємо, що:

S – менший термін (є суб’єктом висновку);

Р – більший термін (є предикатом у висновку);

М – середній термін (термін, що є в обох засновках, але відсутній у висновках).

Тобто, структуру наведеного категоричного силогізму можна записати так:

М – Р

S – M

S – P

Середній термін М виконує роль сполучної ланки між більшим і меншим термінами, завдяки йому стає можливим із двох суджень (засновків) вивести третє судження (висновок), котре є новим знанням.

Слід звернути увагу на такий важливий момент: менший і більший терміни позначаються такими ж символами, як суб’єкт (S) і предикат (Р) судження, проте у силогізмі йдеться лише про терміни висновку, тому ці символи треба застосовувати у вказаному значенні (до суб’єкта і предиката висновку).

В основі висновку в категоричному силогізмі лежить загальне правило, яке називають аксіомою силогізму: “Все, що належить до загального, належить і до часткового, яке входить до обсягу цього загального”. Це означає, що всі ознаки, властиві родовому поняттю, належать і видовим поняття, що входять до роду, іншими словами, “ознака ознаки речі є ознакою самої речі”.

Щоб простий категоричний силогізм був правильний, необхідно брати істинні посилки і дотримуватися ряду правил силогізму, що стосуються термінів і посилок. Але потрібно зазначити, що можливі випадки, коли засновки хибні, а висновок істинний. Наприклад:

Вовки суть травоїдні.

Корови суть вовки.

Корови суть травоїдні.

Правила вживання термінів простого категоричного силогізму

1. У кожному силогізмі повинно бути тільки три терміни S, M і Р. Порушення цього правила призводить до логічної помилки, яка має назву “почетверіння термінів”.

Наприклад:

Закони (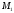) є об’єктивні і вони не залежать від волі й бажання людей (Р).

Конституція України (S) є законом ().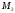

Отже, Конституція України (S) не залежить від волі й бажання людей (Р).

У цьому силогізмі не три, а чотири терміни, оскільки слово “закон” використовується в засновках із різним значенням. У більшому засновку під “законом” ми розуміємо “об’єктивний закон дійсності”, а в меншому – “юридичний закон”. Отже, середній термін у цьому силогізмі відсутній, тому й висновок є хибним.

2. Середній термін має бути розподіленим принаймні в одному із засновків. Якщо середній термін нерозподілений, то висновок зробити не можна. Наприклад: (1) Деякі натуралісти спостережливі.

(2) Всі фізики суть натуралісти.

Отже, всі фізики спостережливі.

Перший засновок є частковостверджувальним судженням, в якому і суб’єкт, і предикат є нерозподіленими. Середній термін (М) не входить ні до одного із засновників, тобто він не зв’язує більший термін з меншим. Внаслідок чого не може бути певного висновку.

Розглянемо інший приклад:

Всі великі поети мають сильну уяву.

Всі великі поети – вразливі люди.

? ? ? ? ? ?

Тут не можна зробити висновок про те, що “Всі вразливі люди мають сильну уяву”. Тут істинним буде частковий висновок: “Деякі вразливі люди мають сильну уяву”. Із засновків видно, що в обсяг Р безумовно входить вся та частина обсягу S, що зайнята обсягом М. Тому засновки дають правильний висновок: “Деякі S належать до обсягу Р”. Отже, ми можемо сформулювати слідуюче правило.

3. Термін, який є нерозподіленим у засновку, не може бути розподіленим у висновку.

Наприклад:

Всі люди дихають киснем.

Земноводні – не люди.

Отже, вони не дихають киснем.

Саме це правило порушене у наведеному вище прикладі: більший термін “ті, хто дихає киснем” був нерозподіленим у засновку (як предикат стверджувального судження), а у висновку став розподіленим (як предикат заперечного судження). Цей силогізм неправильний, бо неналежність земноводних до людей не є достатньою підставою для твердження, ніби земноводні не належать до тих, хто дихає киснем, оскільки “ті, хто дихає киснем” є поняттям родовим стосовно поняття “людина”.

Помилки цього типу називають “недозволеним розширенням більшого терміна”, оскільки в засновку він мислився не в повному обсязі, а у висновку – в повному. При порушенні правила силогізму щодо крайнього терміна трапляється й помилка “недозволеного розширення меншого терміна”.

Хибність цього силогізму можна довести і шляхом графічного зображення співвідношення обсягів його термінів (Схема 3). Поняття “земноводні”, крім вказаних на схемі випадків, можна розглядати ще й як перехресне стосовно “тих, хто дихає киснем”, як таке, в якому мисляться не тільки всі, хто дихає киснем, крім людей, але й ті, хто не дихає киснем (принаймні деякі з них) тощо.

Схема 3.

Правила посилок (засновків) простого категоричного силогізму

1. Із двох заперечних посилок (засновків) не можна зробити ніякого висновку.

Прикладом порушення цього правила може бути наведений силогізм:

Трапеції (М) не є ромби (Р).

Квадрати (S) не є трапеції (М).

? ? ? ? ?

У цьому прикладі середній термін не зв’язує ні суб’єкт, ні предикат, а тому висновок зробити не можна.

2. Якщо одна з посилок (засновків) заперечна, то і висновок повинен бути заперечним, і навпаки, для отримання заперечного висновку необхідно, щоб один із засновків був заперечним.

Наприклад:

Жодне М не є Р.

Всі S є М.

Отже, …

3. Із двох часткових суджень висновку зробити не можна.

Наприклад:

Деякі М є Р	Деякі М є Р
Деякі S є М	Деякі S не є Р

4. Із двох стверджувальних посилок не можна зробити заперечного висновку.

5. Якщо один із засновків є частковим судженням, то і висновок має бути частковим.

Фігури і модуси простого категоричного силогізму та їх різновиди

Залежно від того, яке місце у посилках (засновках) займає середній термін М щодо Р (більшої посилки) і S (меншої посилки), категоричний силогізм набуває чотири фігури, або форми. Перші три фігури вивів ще Арістотель. Кожна фігура має свої особливі правила, які можна обґрунтувати, посилаючись на правила термінів.

Першою називають таку фігуру силогізму, в якій середній термін (М) займає місце суб’єкта в більшому засновку і місце предиката – в меншому.

Схема першої фігури:

М Р

S М

Наприклад: Усі студенти (М) люблять логіку (Р).

Іванова (S) – студентка (М).

Отже, Іванова (S) – любить логіку (Р).

Правила першої фігури:

1. Більша посилка (засновок) повинна бути загальним судженням. Зазначимо, що суб’єкт більшого засновку повинен бути розподіленим, оскільки він виконує роль середнього терміна.

2. Менша посилка (засновок) повинна бути стверджувальним судженням.

Другою називають таку фігуру силогізму, в якій середній термін (М) займає місце предиката і в більшому, і в меншому засновках.

Схема другої фігури:

Р М

S М

Наприклад: Жодна книга (Р) не є періодичним виданням (М).

Журнал (S) є періодичне видання (М).

Журнал (S) не є книга (Р).

Правила другої фігури:

1. Більша посилка (засновок) повинна бути загальним судженням.

2. Одна з посилок (засновків) повинна бути заперечним судженням.

Третьою називають таку фігуру силогізму, в якій середній термін займає місце суб’єкта і в більшому, і в меншому засновках.

Схема третьої фігури:

М Р

М S

Наприклад: Електрон (М) має негативний заряд (Р).

Електрон (М) – елементарна частка (S).

Деякі елементарні частки (S) мають негативний заряд (Р).

Правила третьої фігури:

1. Менша посилка (засновок) повинна бути стверджувальним судженням.

2. Висновок має бути частковим судженням.

Четвертою називають таку фігуру силогізму, в якій середній термін займає місце предиката в більшому засновку і суб’єкта – в меншому.

Схема четвертої фігури:

Р М

М S

У практиці мислення четвертою фігурою користуються вкрай рідко і звичайно її зводять до третьої фігури.

Наприклад:

Всі письменники – художники.

Деякі художники – класики.

Деякі художники – класики.

Правила четвертої фігури:

1. Якщо один із засновків – заперечне судження, то більший засновок – загальне судження.

2. Якщо більший засновок – стверджувальне судження, то менший – загальне судження.

3. Якщо менший засновок – стверджувальне судження, то висновок – часткове судження.

Усі силогізми другої, третьої і четвертої фігур можна перетворити в силогізм першої фігури за допомогою операцій перетворення і обертання. Така процедура називається зведенням силогізмів.

Кожна фігура силогізму має певні модуси (різновиди), що залежать від самої структури силогізму, тобто від тих суджень А, І, О, Е, які входять до його складу.

Модусами фігур силогізму називають різновиди фігур силогізму, що відрізняються за кількісною і якісною характеристиками посилок (засновків). Модус (з латинської – міра, норма, різновид) дає змогу встановити хибний висновок. Усіх модусів може бути 64, однак, лише за тієї умови, коли основою поділу є тільки кількісна і якісна специфіка складового силогізму – його засновків і висновків. Якщо ж за основу поділу взяти як згадані ознаки, так і місце середнього терміна, то одержимо 256 модифікацій силогізму. Однак, деякі з них повторюються, тому залишається лише 19, з яких практично використовують 14 (5 модусів четвертої фігури зводяться до інших).

Модуси першої фігури категоричного силогізму: ААА; ЕАЕ; АІІ; ЕІО.

Модуси другої фігури категоричного силогізму: ЕАЕ; АЕЕ; ЕІО; АОО.

Модуси третьої фігури категоричного силогізму: ААІ; ІАІ; АІІ; ЕАО; ОАО; ЕІО.

Модуси четвертої фігури категоричного силогізму: ААІ; АЕЕ; ІАІ; ЕАО; ЕІО.

Наприклад:

Модус ААА

І фігура	ІІ фігура	ІІІ фігура	IV фігура
Всі М є Р	Всі Р є М	Всі М є Р	Всі Р є М
Всі S є М	Всі S є М	Всі М є S	Всі М є Р
Всі S є Р	Всі S є Р	Всі S є Р	Всі S є Р

Правильними є наступні модуси щодо кожної фігури:

І фігура	ІІ фігура	ІІІ фігура	IV фігура
ААА (Barbara) EAE (Celarent) AII (Darii) EIO (Ferio)	EAE (Cesare) AEE (Camestres) EIO (Festino) AOO (Baroko)	AAI (Darapti) IAI (Disamis) AII (Datisi) EAO (Felapton) OAO (Bocardo) EIO (Ferison)	AAI (Bramantipi) AEE (Camenes) IAI (Dimaris) EAO (Fesapo) EIO (Fresison)

Кожний правильний модус категоричного силогізму має свою назву, в якій голосні літери означають якісну і кількісну характеристику засновків і висновків.

Перша фігура

Barbara (AAA)

„Всякий, кто оставляет умирать с голоду тех, кого он должен накормить, – убийца.

Все богатые, которые не жертвуют на общественные нужды, оставляют умирать с голоду тех, кого они должны накормить.

Следовательно, они убийцы”.

Celarent (EAE)

Жодна планета не світить власним світлом.

Юпітер – планета.

Отже, Юпітер не світить власним світлом.

Darii (AII)

Всі метали проводять електричний струм.

Деякі рідини є металами.

Отже, деякі рідини проводять електричний струм.

Ferio (EIO)

Жоден раб не є вільною людиною.

Деякі люди є рабами.

Отже, деякі люди не є вільними.

Друга фігура

Cesare (EAE)

„Ни один лжец не заслуживает доверия.

Всякий добропорядочный человек заслуживает доверия.

Ни один добропорядочный человек не лжец”.

Camestres (AEE)

Кожний простий категоричний силогізм має три терміни.

Даний умовивід не має трьох термінів.

Отже, цей умовивід не є простим категоричним силогізмом.

Festino (EIO)

Жодна серйозна людина не є легковажною.

Деякі люди є легковажними.

Отже, деякі люди не є серйозними.

Baroko (AOO)

„Всякой добродетели сопутствует скромность.

Бывает рвение без скромности.

Следовательно, бывает рвение, которое не есть добродетель”.

Третя фігура

Darapti (AAI)

„Бесконечная делимость материи непостижима.

Бесконечная делимость материи не подлежит сомнению.

Есть не подлежащие сомнению истины, которые непостижимы”.

Felapton (EAO)

„Ни один человек не может уйти от самого себя.

Всякий человек – враг самому себе.

Есть враги, от которых не уйти”.

Disamis (IAI)

„Есть злые люди, обладающие огромным состоянием.

Все злые люди несчастны.

Есть несчастные, обладающие огромным состоянием”.

Bocardo (ОАО)

„Есть гнев, который не предосудителен.

Всякий гнев – страсть.

Есть страсти, которые не предосудительны”.

Ferison (EIO)

„Никакая глупость не красноречива.

Есть глупости, выраженные посредством фигур.

Есть фигуры, которые не красноречивы”.

Четверта фігура

Bramantip (ААІ)

Всі метали – є речовинами.

Всі речовини мають вагу.

Деякі тіла, що мають вагу, суть метали.

Camenes (АЕЕ)

Всі квадрати є паралелограми.

Жодний паралелограм не є трапецією.

Жодна трапеція не є квадратом.

Fresison (ЕІО)

Жодна доброчесність не заперечує любові до істини.

Існує любов до спокою, яка заперечує любов до істини.

Отже, існує любов до спокою, яка не є доброчесністю.

Dimaris (IAI)

Деякі філософи є політиками.

Всі політики дуже амбіціозні люди.

Деякі амбіціозні люди є філософами.

Fesapo (EAO)

Жоден аспірант не є студентом.

Всі студенти повинні складати іспити.

Деякі особи, які повинні складати іспити, – не аспіранти.

(Деякі приклади в лапках ми взяли із книги А. Арно і П. Ніколь „Логика, или Искусство мыслить”.)

Скорочений силогізм (ентимема)

Опосередкований дедуктивний умовивід, як ми бачили раніше, складається з двох засновків і висновку. Але в процесі мислення умовиводи іноді будуються в скороченому вигляді, тобто не висловлюють або не встановлюють усіх трьох частин. Л. Фейєрбах вважав, що дотепна манера писати полягає в тому, що висловлюється не все, оскільки передбачається наявність розуму і в читача. Умовивід, у якому пропущена одна з його частин, але яка мається на увазі, називається скороченим умовиводом або ентимемою. Термін „ентимема” у перекладі з грецького означає „у розумі”, „у думках”. Ентимеми бувають із пропущеною більшою посилкою, із пропущеною меншою посилкою, і з пропущеним висновком.

Наведемо приклад ентимеми з пропущеною більшою посилкою: „Це слово утворене від дієслівної основи, тому що є дієприкметником”.

У нескороченій формі воно буде мати такий вигляд:

Всі дієприкметники утворені від дієслівної основи.

Дане слово – дієприкметник.

Отже, дане слово утворене від дієслівної основи.

Приклад ентимеми з пропущеною меншою посилкою: „Всі власні імена пишуться з прописної букви, отже, "Мінськ" пишеться з прописної букви”.

У нескороченій формі даний умовивід має вигляд:

Всі власні імена пишуться з прописної букви.

Мінськ – власне ім'я

Отже, "Мінськ" пишеться з прописної букви.

Приклад ентимеми з пропущеним висновком: "Всі спортсмени витривалі, а Петров – спортсмен."

Повна форма даного висновку має такий вигляд:

Всі спортсмени витривалі.

Петров – спортсмен.

Отже, Петров – витривалий.

Ентимеми можуть включати не тільки категоричні, але й умовні і розділові судження.

Наприклад: "Мідь піддана тертю, отже, вона нагрівається."

У даному випадку ентимема умовно-категоричного умовиводу із опущеною умовною посилкою: "Якщо мідь піддати тертю, то вона нагріється."

Щоб відновити силогізм, необхідно, перш за все, визначити, що в ньому пропущено – один із засновків, чи висновок. Зовнішня ознака, чим є те, чи інше судження – засновком чи висновком, виступають відповідні сполучники.

Посилка (засновок), звичайно, стоїть після сполучників „оскільки”: „тому що”, „бо” і т.д., а висновок стоїть після слів: "отже", "тому", "тому що".

Наприклад: „Цей фізичний процес не є випаром, тому що не відбувається перехід речовини з рідини в пар”.

Сформулюємо повний категоричний силогізм:

Випаровування є процес переходу речовини з рідини в пар.

Цей фізичний процес не є переходом речовини з рідини в пар.

Отже, цей фізичний процес не є випаровуванням.

Приведений категоричний силогізм побудований по ІІ фігурі: одна з посилок і висновок є заперечувальним судженням, велика посилка є теж судження.

Якщо судження в ентимемі незалежні одне від одного і виражені складносурядними реченнями, то в ній пропущено висновок.

З’ясувавши, яка частина силогізму пропущена, необхідно його відновити.

Полісилогізмом називаються два або кілька простих категоричних силогізмів, зв’язаних один з одним таким чином, що висновок попереднього силогізму (просилогізму) стає засновком наступного силогізму (епісилогізму). Розрізняють прогресивний і регресивний полісилогізми.

У прогресивному (поступальному) полісилогізмі висновок попереднього стає більшим засновком наступного силогізму. Схема прогресивного полісилогізму така:

Всі А є В.

Всі С є А.

Наприклад:

Всі метали (А) електропровідні (В).

Лужноземельні метали (С) – метали (А).

Всі С є В.

Всі Д є В.

Всі Д є В.

Лужноземельні метали (С) – електропровідні (В).

Кальцій (Д) – лужноземельний метал (В).

Кальцій (Д) – електропровідний (В).

Регресивний (зворотний) полісилогізм – це такий складний силогізм, у якому висновок попереднього силогізму стає меншою посилкою наступного силогізму, а думки рухаються від менш загального до більш загального.

Загальна схема регресивного полісилогізму для загальностверджувальних посилок має вигляд:

Всі В суть С.

Всі А суть В.

Всі С суть Д.

Всі А суть С.

Всі А суть Д.

Складноскорочені силогізми

Прогресивний і регресивний полісилогізми дуже часто використовуються у скороченій формі – у вигляді соритів.

Сорит (нагромаджений, купа) – складноскорочений силогізм, у якому не висловлюють, а тільки мають на увазі більші або менші засновки і всі висновки, крім останнього.

Розрізняють сорити двох видів: прогресивний (гокленієвський) і регресивний (аристотелівський).

Гокленієвський сорит – прогресивний полісилогізм, у якому пропущено всі більші засновки, крім першого, та всі висновки, крім останнього.

Традиційний приклад:

Тварина є субстанція.

Чотириноге є тварина.

Кінь є чотириноге.

Буцефал є кінь.

Буцефал є субстанція.

У гокленієвському сориті в першому засновку є термін, який відіграє роль предиката у висновку, а в останньому засновку – термін, який займає місце суб’єкта у висновку.

Якщо відновити цей складноскорочений силогізм, то ми одержимо цілу низку простих силогізмів, поєднаних в один полісилогізм.

1.	Тварина є субстанція. Чотириноге є тварина. Чотириноге є субстанція.
2.	(Чотириноге є субстанція). Кінь є чотириноге. Кінь є субстанція.
3.	(Кінь є субстанція). Буцефал є кінь. Буцефал є субстанція.

Аристотелівський сорит – регресивний полісилогізм, у якому пропущено всі менші засновки, крім першого, і всі висновки, крім останнього.

Знову беремо традиційний приклад:

Буцефал є кінь.

Кінь є чотириноге.

Чотириноге є тварина.

Тварина є субстанція.

Буцефал є субстанція.

В аристотелівському сориті об’єкт висновку беруть з першого засновку, а його предикат – з останнього.

Відновивши цю різновидність сориту, одержимо такі складові полісилогізму:

1.	Кінь є чотириноге. Буцефал є кінь. Буцефал є чотириноге.
2.	Чотириноге є тварина. (Буцефал є чотириноге). Буцефал є тварина.
3.	Тварина є субстанція. (Буцефал є тварина). Буцефал є субстанція.

Отже, схема прогресивного сориту:

Всі А суть В.

Всі С суть А.

Всі Д суть С.

Всі Е суть Д.

Всі Е суть В

Схема регресивного сориту:

Всі А суть В.

Всі В суть С.

Всі С суть Д.

Всі А суть Д.