
- •Міністерство освіти і науки України
- •Дніпропетровська державна фінансова академія
- •Програма навчальної дисципліни
- •1. Мета та завдання навчальної дисципліни
- •2. Інформаційний обсягнавчальної дисципліни модуль і. Математичні моделі у фінансах
- •Тема 1. Регресійні моделі дослідження фінансової діяльності на регіональному і державному рівні
- •Тема 2. Моделювання фінансової діяльності із застосуванням виробничих функцій та методів диференційного числення
- •Тема 3. Дослідження моделей оптимізації фінансової діяльності за допомогою методів математичного програмування
- •Тема 4. Імовірнісні моделі у фінансах
- •Тема 5. Arima-моделі та моделі лонгітюдних даних
- •Тема 6. Методи багатовимірного статистичного аналізу
- •Питання для самоконтролю
- •Завдання до самостійної роботи Завдання 1
- •Завдання 2
- •Завдання 3
- •Завдання 4
- •Рекомендована література
- •Питання для самоконтролю
- •Завдання до самостійної роботи Завдання 1
- •Завдання 2
- •Рекомендована література
- •[1, 2, 4, 8]
- •Тема 3. Дослідження моделей оптимізації фінансової діяльності за допомогою методів математичного програмування
- •План вивчення теми
- •Навчальні цілі
- •Завдання та методичні рекомендації до вивчення теми
- •Питання для самоконтролю
- •Завдання до самостійної роботи Завдання 1
- •Завдання 2
- •Рекомендована література
- •Питання для самоконтролю
- •Завдання до самостійної роботи Завдання 1
- •Завдання 2
- •Завдання 3
- •Питання для самоконтролю
- •Завдання для самостійного виконання
- •Рекомендована література
- •Завдання та методичні рекомендації до вивчення теми
- •Навчальні цілі
- •Завдання 1
- •Завдання 2
- •Завдання 3
- •Методичні рекомендації до практичного заняття
- •Контрольні завдання Завдання 1
- •Завдання 2
- •Завдання 3
- •Завдання 4
- •Рекомендована література
- •Завдання 2
- •Завдання 3
- •Методичні рекомендації до практичного заняття
- •Контрольні завдання Завдання 1
- •Завдання 2
- •Рекомендована література
- •Завдання №2
- •Завдання №3
- •Завдання №4
- •Завдання №5
- •5. Контрольні заходи
- •6. Література
- •Математичні моделі у фінансах
Тема 2. Моделювання фінансової діяльності із застосуванням виробничих функцій та методів диференційного числення
Застосування еластичності в аналізі фінансової діяльності підприємства. Геометрична інтерпретація еластичності. Граничні (маржинальні) і середні значення показника. Коефіцієнт еластичності.
Виробничі функції, їх властивості. Еластичність заміщення факторів.
Математична теорія фірми. Задачі на максимум прибутку або випуску при досконалій конкуренції та монополії. Оптимальний розв’язок. Граничні витрати. Граничний дохід.
Тема 3. Дослідження моделей оптимізації фінансової діяльності за допомогою методів математичного програмування
Виробнича задача оптимізації економічного показника при наявних обмеженнях ресурсів. Оптимальна модель планування виробництва. Оптимальний розподіл ресурсів.
Економічна інтерпретація пари спряжених задач. Аналіз рентабельності продукції та дефіцитності ресурсів. Аналіз обмежень дефіцитних і недефіцитних ресурсів. Аналіз коефіцієнтів цільової функції та матриці обмежень. Використання двоїстих оцінок в аналізі економічних задач.
Оптимізаційні задачі планування фінансів на підприємствах та в установах.
Задачі розподільчого типу з використанням бінарних змінних.
Тема 4. Імовірнісні моделі у фінансах
Кількісні показники ступеня ризику. Ризик в абсолютному вираженні. Ризик у відносному вираженні. Класичний та неокласичний підходи у визначенні ризику. Ступінь та зони допустимого, критичного та катастрофічного ризику. Ризик і нерівність Чебишева. Оцінка систематичного ризику.
Оцінка, порівняння проектів відносно ступеня ризику.
Елементи теорії гри. Оцінка ризику за критеріями Бейесса, Гурвица, Лапласа, Ходжеса-Лемана Вальда, Севиджа.
Змістовий модуль 2. Сучасні моделі і методи емпіричних досліджень і прогнозування в фінансовій діяльності підприємств та установ
Тема 5. Arima-моделі та моделі лонгітюдних даних
Застосування ARIMA-моделей в емпіричних дослідженнях. Лагові змінні. Базові форми ARIMA-моделей: авторегресійні моделі різних порядків, модель ковзного середнього. Прогнозування за допомогою ARIMA-моделей. Приклади застосування: моделювання доходів місцевих бюджетів в регіоні; прогнозування обсягів податкових надходжень в регіоні з урахуванням ризику.
Панельні (лонгітюдні) дані. Оцінювання параметрів регресійних моделей у випадку панельних даних. Особливості використання інструментальних змінних в моделях з панельними даними. Моделі з фіксованими та випадковими ефектами. Сучасні пакети STATA,SPSSSTATISTICA,E.VIEWS. Приклади застосування регресій з панельними даними: моделювання бюджетних надходжень та витрат на регіональному рівні.
Тема 6. Методи багатовимірного статистичного аналізу
Факторний аналіз. Метод головних компонент. Кластерний аналіз.
Застосування методів багатовимірного статистичного аналізу в моделюванні та обчисленні рейтингу. Моделювання рейтингового оцінювання за допомогою інтегрального показника на прикладах якості життя населення та розвитку страхування в регіонах України.
МОДУЛЬ ІІ
Індивідуальне науково-дослідне завдання (ІНДЗ).
Завдання та методичні рекомендації до самостійної роботи
Перелік основних видів самостійної роботи з дисципліни: опрацювання теоретичного матеріалу, розв’язування задач, відповіді на контрольні питання.
Модуль І. Математичні моделі у фінансах
Змістовий модуль 1. Базові економіко-математичні моделі в дослідженні фінансової діяльності підприємств та установ
Тема 1. Регресійні моделі дослідження фінансової діяльності на регіональному і державному рівні
План вивчення теми
Оцінка параметрів простої і множинної лінійної регресії, перевірка моделі на адекватність та прогнозування за моделлю.
Перетворення нелінійних регресій у лінійні.
Застосування регресійних моделей у прикладних задачах на регіональному і державному рівні.
Навчальні цілі
Ознайомити студентів з задачами економічного і фінансового аналізу, які розв’язуються на основі регресійних економетричних моделей.
Завдання та методичні рекомендації до вивчення теми
Докладно питання побудови різних регресій (парних та множинних лінійних, квазілінійних, нелінійних відносно факторів і параметрів, з фіктивними змінними) розглянуті в навчально-методичному посібнику «Економіко-математичні методи та моделі. Частина 2» [4].
Повторимо основні етапи побудови і аналізу лінійної парної регресії на прикладі.
Приклад. Дохід підприємства Y ( тис. грн.) наведено в таблиці:
|
Х, рік |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
|
Y, дохід |
2800,0 |
6171,0 |
7192,0 |
4929,0 |
8202,0 |
8891,5 |
10180,6 |
11260,0 |
13440,0 |
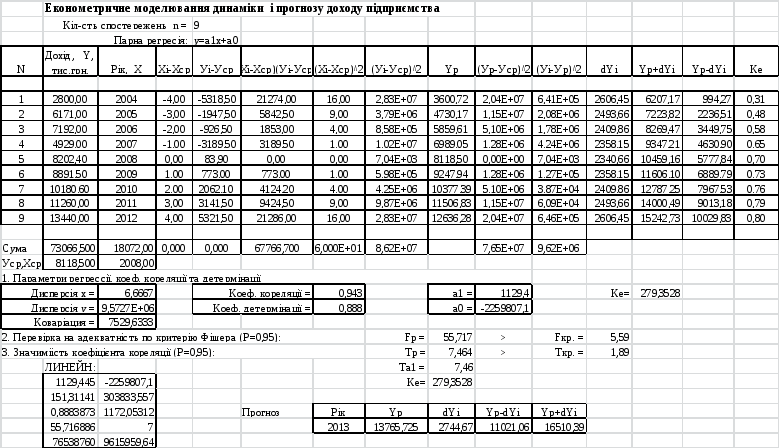
Побудуємо діаграму розподілу на основі даних спостережень. Точки спостережень групуються навколо вдаваної прямої (див. рис. на с.11, розрахунок – на с. 12). Тому припустимо, що дані спостережень наближено можна описати лінійною залежністю між фактором Х та показником Y. Побудуємо парну лінійну регресійну модель:
![]() ,
,![]() (1)
(1)
де
![]() – параметри, які треба визначити;
– параметри, які треба визначити;
![]() – відхилення фактичних значень
– відхилення фактичних значень![]() від їх оцінки
від їх оцінки![]() ;
;
![]() - кількість спостережень.
- кількість спостережень.
Параметри
![]() визначимо методом найменших квадратів,
згідно з яким, сума квадратів різниць
визначимо методом найменших квадратів,
згідно з яким, сума квадратів різниць![]() має бути мінімальною для найкращого
наближення, яке забезпечує регресія
, тобто
має бути мінімальною для найкращого
наближення, яке забезпечує регресія
, тобто
![]() .
.
За допомогою вказаного методу отримані значення параметрів:
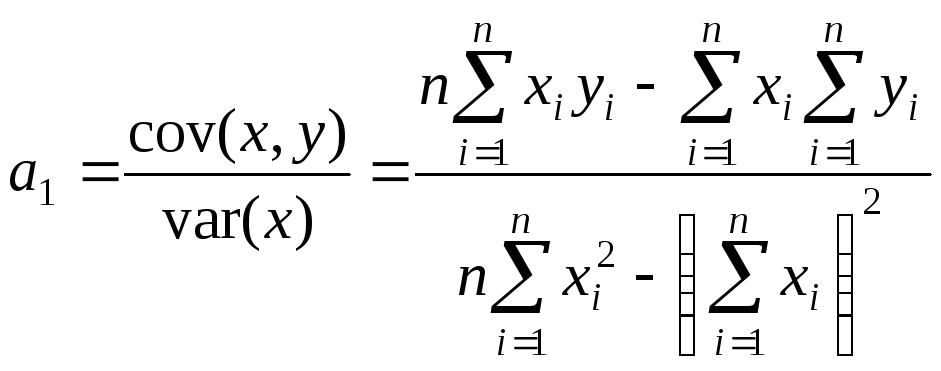 =-2259807,1, (2)
=-2259807,1, (2)
 = 1129,445, (3)
= 1129,445, (3)
де
![]() -
середні значення вибіркових даних.
-
середні значення вибіркових даних.
Отже, розрахункові значення показника обчислюються за формулою:
![]() -2259807,1 + 1129,445хі.
-2259807,1 + 1129,445хі.
Середньоквадратична помилка регресії:
 = 1172,05. (4)
= 1172,05. (4)
Відносно середнього вибіркового
значення
![]() =
8118,5 це становить 14,4 %.
=
8118,5 це становить 14,4 %.
Коефіцієнт кореляції R обчислюється за формулою :
 .
(5)
.
(5)
Для даної моделі R=0,94означає, що між фактором та показником існує тісний додатний зв'язок.
Коефіцієнт детермінації для даної моделі дорівнює
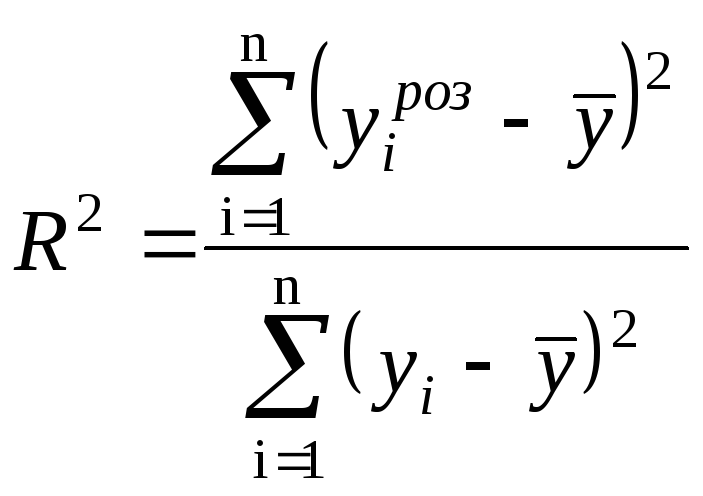 = 0,89.
(6)
= 0,89.
(6)
Таким чином, згідно з обраною моделлю, залежність показника Y пояснюється саме фактором Х, залученим у модель, з урахуванням специфікації моделі, на 89%.
Перевіримо адекватність побудованої лінійної моделі за критерієм Фішера. Для цього розрахуємо значення F-критерію згідно з моделлю:
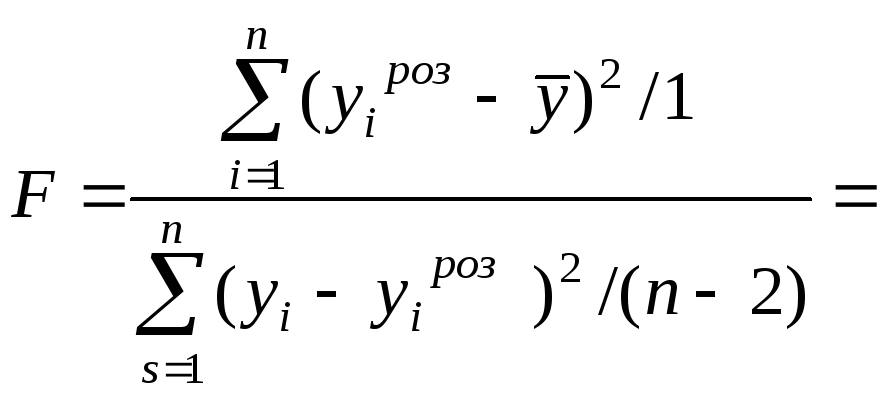 55,72.
(7)
55,72.
(7)
За статичними таблицями F-розподілу
Фішера для 5%-ого рівня значимості
(задаємо довільно) та при степенях
вільності відповідно 1 (для парної
регресії) і n-2=7 знайдемо критичне
значення![]() 5,59. Таким чином, розраховане значення
F більше, ніж критичне. Отже, можна
зробити висновок про адекватність
побудованої моделі вихідним даним за
F-критерієм Фішера.
5,59. Таким чином, розраховане значення
F більше, ніж критичне. Отже, можна
зробити висновок про адекватність
побудованої моделі вихідним даним за
F-критерієм Фішера.
Із двох оцінених параметрів саме
параметр
![]() визначає степінь залежності показника
від фактора. Тому перевіримо його
статистичну значимість. Це можна зробити
за допомогою критерію Стьюдента.
Розрахункове значення t-статистики
отримаємо як відношення
визначає степінь залежності показника
від фактора. Тому перевіримо його
статистичну значимість. Це можна зробити
за допомогою критерію Стьюдента.
Розрахункове значення t-статистики
отримаємо як відношення![]() до своєї стандартної похибки
до своєї стандартної похибки![]() :
:
![]() 7,46
, (8)
7,46
, (8)
де
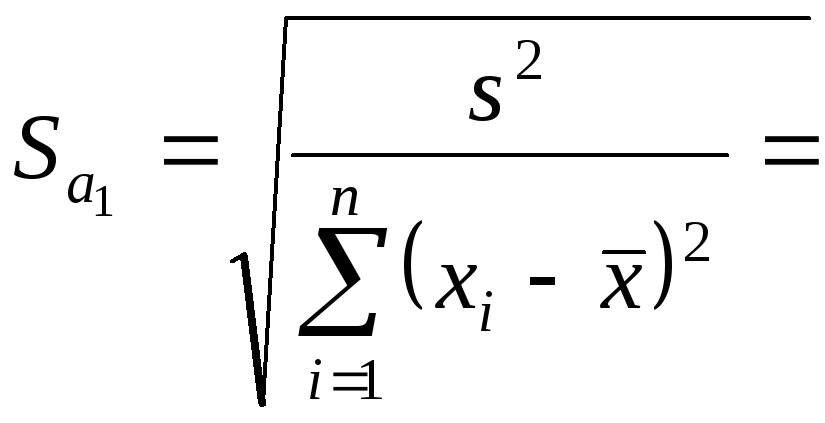 151,3,
151,3,![]() .
(9)
.
(9)
Критичне значення t-статистики знаходимо
за статистичними таблицями t-розподілу
Стьюдента при рівні значимості
![]() 0,1
(задаємо довільно) та ступенях вільностіn-2= 7:
0,1
(задаємо довільно) та ступенях вільностіn-2= 7:![]() 1,89.
1,89.
Таким чином, розрахункове значення
більше, ніж критичне. Отже, параметр
![]() з надійністю 95% (1-α/2) можна вважати
статистично значимим.
з надійністю 95% (1-α/2) можна вважати
статистично значимим.
Для оцінки впливу фактора Х на показник Y без урахування одиниць виміру обчислимо коефіцієнти еластичності для кожного спостереження за формулою
![]() (10)
(10)
та побудуємо діаграму.
Як бачимо, еластичність обсягу реалізації продукції збільшується при збільшенні затрат на рекламу.
Еластичність, що обчислена на основі середніх значень показника і фактора, складає
![]() 0,888.
0,888.
Це означає, що якщо фактор зміниться на 1%, то показник зміниться на 0,888%.
Модель є адекватною, як було показано,
зі статистично значимим параметром
![]() .
Тому її можна використовувати для
прогнозування доходу підприємства.
Визначимо прогноз на наступний 2013 рік.
.
Тому її можна використовувати для
прогнозування доходу підприємства.
Визначимо прогноз на наступний 2013 рік.
Точкову оцінку отримаємо за формулою:
![]() -2259807,1 + 1129,445хпр = 13765,725
(тис. грн.).
-2259807,1 + 1129,445хпр = 13765,725
(тис. грн.).
Далі побудуємо надійний інтервал з
границями (![]() ;
;![]() ),
де
),
де
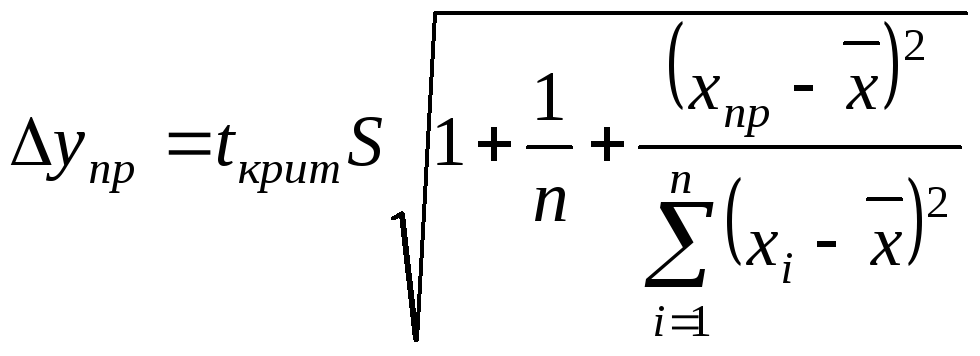 =
2744,67. (11)
=
2744,67. (11)
Границі довірчого інтервалу (11021,06; 16510,39) (тис. грн.) встановлені з надійністю 95%.

Рис. 1 – Регресія, довірча зона і прогнозні оцінки доходу
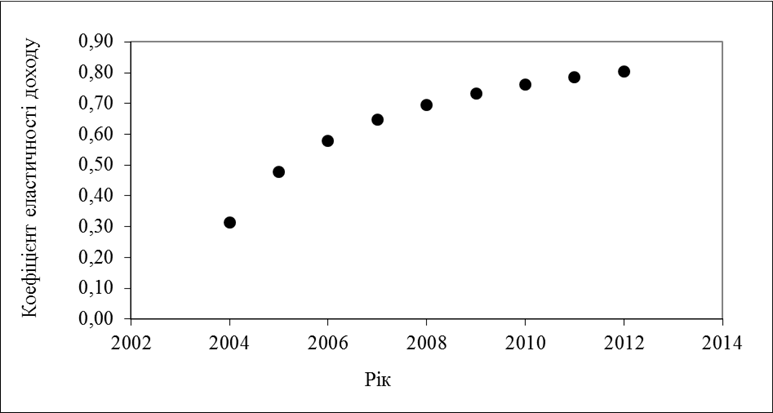
Рис.2 – Коефіцієнт еластичності доходу
Якщо виникає потреба розглядати залежність показника від декількох факторів, треба будувати множинну регресію:
![]() ,
(12)
,
(12)
де
![]() -
показник ,
-
показник ,![]() - фактори,
- фактори,![]() - випадкова величина,
- випадкова величина,
або для
![]() го
спостереження,
го
спостереження,![]() :
:
![]() .
(13)
.
(13)
В моделі мають бути присутніми тільки незалежні фактори. Одним із методів визначення наявності чи відсутності мультиколінеарності (залежності факторів) є побудова матриці парних коефіцієнтів кореляції:
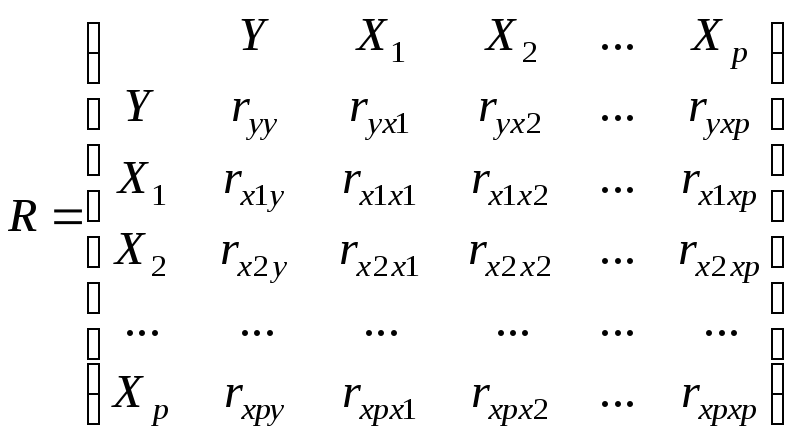 .
(14)
.
(14)
Матриця має властивості: діагональні елементи дорівнюють одиниці; матриця симетрична відносно головної діагоналі. Для розрахунку коефіцієнтів парної кореляції можна користуватися функцією КОРРЕЛ.
Для кожної пари факторів визначають коефіцієнт парної кореляції. Якщо значення коефіцієнта кореляції близько за модулем до одиниці, то між цими факторами існує тісний зв'язок, тобто фактори залежні. Треба виключити один з цих факторів. Виключають той, що має менший вплив на показник, про що свідчать коефіцієнти кореляції між факторами та показником ( у першому рядку матриці).
Параметри регресії визначаються у матричному вигляді наступним чином:
![]() ,
(15)
,
(15)
|
|
|
|
|
|
|
|
|
де
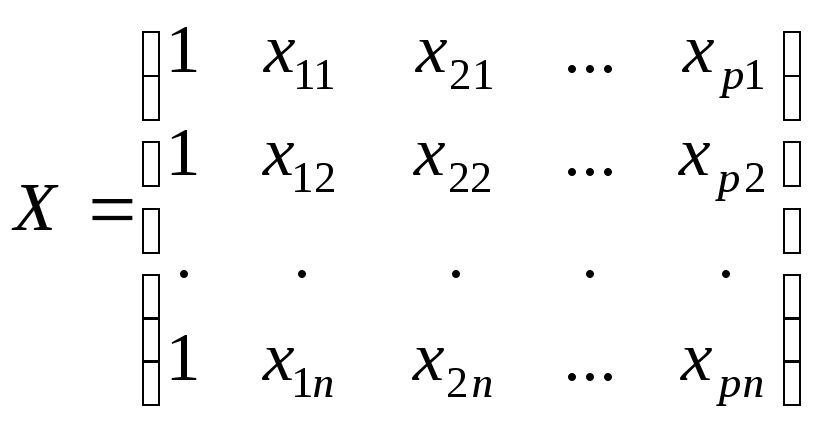 - матриця спостережень за незалежними
змінними;
- матриця спостережень за незалежними
змінними;
![]()
![]() - матриця, транспонована до матриці
- матриця, транспонована до матриці![]() ;
;
![]() - матриця, обернена до матриці
- матриця, обернена до матриці![]() ;
;
 - матриця спостережень за показником
- матриця спостережень за показником![]() ;
;
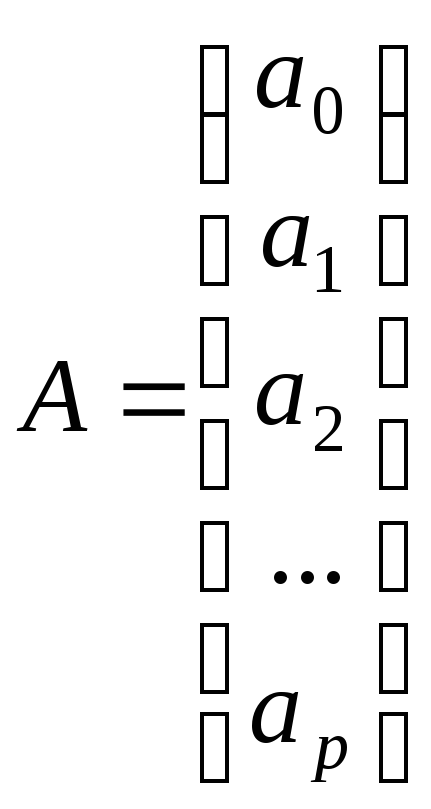 - матриця параметрів регресії;
- матриця параметрів регресії;
![]() - кількість спостережень,
- кількість спостережень,![]() -
кількість факторів.
-
кількість факторів.
Для зменшення степені залежності
коефіцієнту детермінації від кількості
факторів використовують оцінений
коефіцієнт детермінації: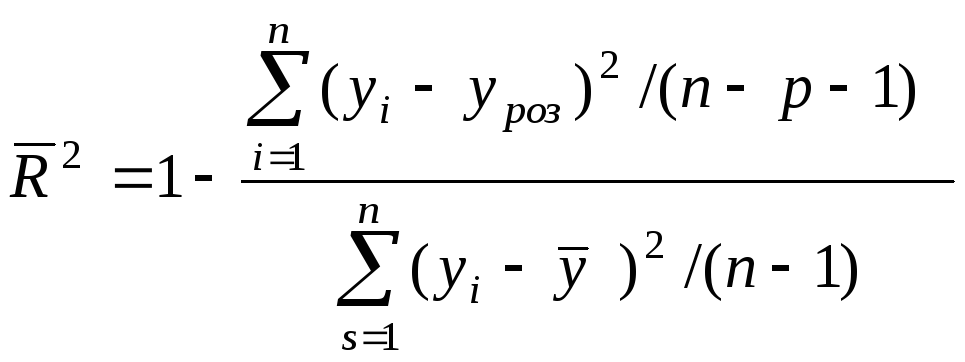 .
(16)
.
(16)
Для перевірки адекватності моделі використовується критерій Фішера, для визначення значимості параметрів регресії – критерій Стьюдента. Розрахункові значення можна отримати за формулами:
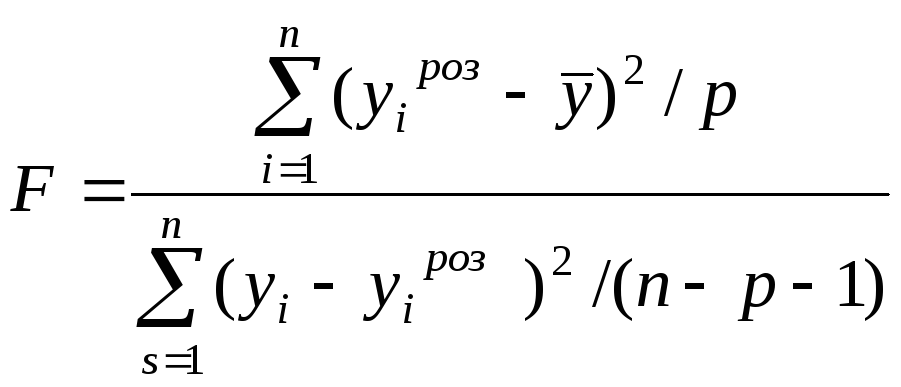 ;
;![]() .
(17)
.
(17)
Для визначення меж довірчих інтервалів показника існує формула:
(![]() ;
;![]() ),
),
![]() , (18)
, (18)
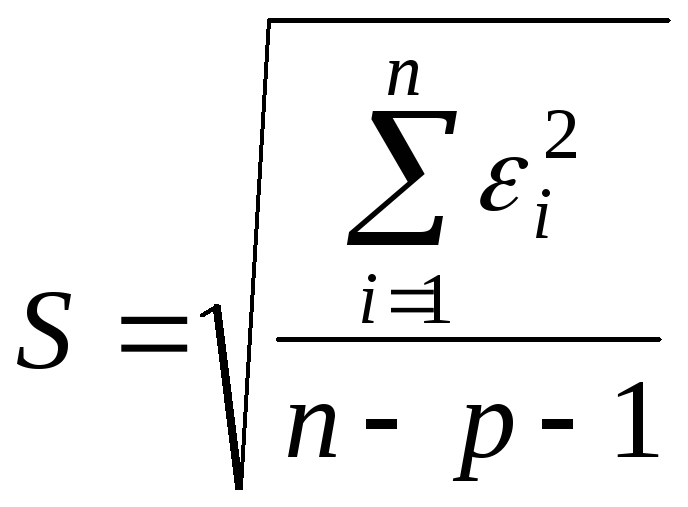 ,
(19)
,
(19)
![]() ,
(20)
,
(20)
де
![]() .
.
Використання деяких функцій в електронних таблицях EXCEL для розрахунку статистики і перевірки лінійної регресійної моделі
Для розрахунку параметрів та статистики моделі можна користуватися статистичною функцією ЛИНЕЙН:
ЛИНЕЙН (известные_значения_y;известные_значения_x;конст;статистика)
Для даної задачі:
известные_значения_y – значення обсягу реалізації продукції (масив значень У)
известные_значения_x – значення витрат на рекламу (масив значеньХ)
конст – значення, яке показує, чи необхідно, щоб константа мала нульове значення (конст має значення ЛОЖЬ, задається значення 0), чи щоб константа обчислювалася звичайним способом (конст має значення ИСТИНА, задається значення 1).
статистика – значення, яке показує, чи необхідно, щоб виводилась додаткова статистика по регресії (конст має значення ИСТИНА, задається значення 1) або треба вивести тільки значення параметрів регресії ( конст має значення ЛОЖЬ, задається значення 0).
Регресійна статистика має вигляд:
|
an |
an-1 |
… |
a1 |
a0 |
|
Sn |
Sn-1 |
… |
S1 |
S0 |
|
R2 |
Sy |
|
|
|
|
F |
Df |
|
|
|
|
ssr |
sse |
|
|
|
де
|
an, an-1,…, a0 |
Параметри регресії |
|
Sn, Sn-1,..., S0 |
Стандартні помилки параметрів an, an-1,…, a0. |
|
R2 |
Коефіцієнт детермінації. |
|
Sy |
Стандартна помилка для оцінки y |
|
F |
F-статистика. |
|
Df |
Ступені вільності |
|
ssr |
Сума квадратів регресії |
|
ssе |
Сума квадратів залишків |
Для розрахунку за допомогою функції ЛИНЕЙНтреба виконати такі дії:
викликати функцію ЛИНЕЙН(fx);
у вікні функції задати значення Х(незалежної змінної - фактора) та значенняУ(залежної змінної – показника); також задати значення статистики (1) та константи (1); Ок;
виділити область: кількість стовпчиків дорівнює кількості параметрів регресії; кількість рядків завжди однакова: 5;
натиснути функціональну клавішу F2;
натиснути одночасно клавіші Ctrl, Shift, Enter.
Критичне значення критерію Фішера знаходяться за допомогою функції FРАСПОБР(α; р; n-р-1) для надійності та при р факторах,
n – кількість спостережень,
Критичне значення критерію Стьюдента обчислюється за допомогою функції СТЬЮДРАСПОБР (α; n-р-1) для надійності 1- α ,
n – кількість спостережень, р – кількість факторів.
Для визначення добутку матриць можна користуватися функцією МУМНОЖ, для обчислення оберненої матриці - функцієюМОБР, для транспонування матриць – функцієюТРАНСП.
Перетворення нелінійних моделей докладно розглянуто в навчально-методичному посібнику «Економіко-математичні методи та моделі. Частина 2» [4].
