2. Елементи комбінаторики

Щоб обчислити ймовірність тієї чи іншої випадкової події для певного класу задач із дискретним і обмеженим простором елементарних подій, необхідно вміти обчислити кількість усіх елементарних подій (елементів множини) і числоелементарних подій, які сприяють появі випадкової події.

Існує клас задач, в яких для обчислення івикористовуються елементи комбінаторики: переставлення, розміщення та комбінації. У комбінаториці оперують множинами однотипних елементів.

Загалом множини бувають упорядковані та невпорядковані.

Множину називають упорядкованою, якщо при її побудові істотним є порядок розміщення елементів. У противному разі множину називають невпорядкованою.

Переставлення. Переставленнями із елементів називають такі впорядковані множини зелементів, які різняться між собою порядком їх розміщення.

Кількість таких упорядкованих множин обчислюється за формулою

, (2.2)

де набуває лише цілих невід'ємних значень.

Приймають, що 1! =1 і 0!=1.

Приклад 1. Задано множину цілих чисел = {1, 2, 3, 4, 5}. її елементи навмання розставляють у рядок. Обчислити ймовірності таких випадкових подій:

А — розставлені в ряд числа утворюють зростаючу послідовність;

В — спадну послідовність;

С — цифра 1 стоятиме на першому місці, а 5 — на останньому;

Розв'язання. Простір елементарних подій для цього експерименту міститиме =5!=1·2·3·4·5=120 несумісних, рівноможливих елементарних подій.

Кількість елементарних подій, що сприяють появі А дорівнює одиниці (= 1). Кількість елементарних подій, що сприяють появі В дорівнює одиниці (= 1). Для випадкової події С= 3!. Тоді

, ,.

Розміщення. Розміщеннями із n елементів по m (0 < m < n) називаються такі впорядковані множини, кожна з яких містить m елементів і які відрізняються між собою порядком розташування цих елементів або хоча б одним елементом.

Кількість таких множин обчислюється за формулою

. (2.3)

Наприклад, = 9 ·8 ·7 = 504 .

Комбінації. Комбінаціями з n елементів по m (0 < m < n) називаються такі множини з m елементів, які різняться між собою хоча б одним елементом.

Кількість таких множин

. (2.4)

3. Геометрична ймовірність

Класичне означення ймовірності придатне лише для експериментів з обмеженим числом рівноможливих елементарних подій, тобто коли множина її (простір елементарних подій) обмежена.

Якщо множина є неперервною і квадровною, то для обчислення ймовірностіА (А) використовується геометрична ймовірність

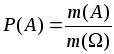. (2.5)

Якщо множина вимірюється в лінійних одиницях, тодорівнюватиме відношенню довжин, якщовимірюється у квадратних одиницях, то Р (А) дорівнюватиме відношенню площ, і т. ін.

Приклад. По трубопроводу довжиною 2 км між пунктами А і В перекачують нафту. Яка ймовірність того, що пошкодження (якщо воно відбудеться) через деякий час роботи трубопроводу станеться на певній ділянці довжиною 100 м.

Розв'язання. Простір елементарних подій , тоді . Згідно з (2.5) маємо:

.

4. Статистична ймовірність

На практиці обчислити ймовірності випадкових подій можна лише для обмеженого класу задач як для дискретних, так і для неперервних просторів елементарних подій (множини ). Для більшості задач, особливо економічних, обчислити ймовірності практично неможливо. У цьому разі використовується статистична ймовірність.

Насамперед уводиться поняття відносної частоти випадкової події .

Відносною частотою випадкової події А називається відношення кількості експериментівm, при яких подія А спостерігалася, до загальної кількості n проведених експериментів:

. (2.6)

Як і для ймовірності випадкової події, для відносної частоти виконується нерівність .

Статистичною ймовірністю випадкові події називається константа навколо якої групуються відносні частоти випадкової події.