Література

Обов’язкова: [1]. Додаткова:[1], [4], [7].

Практичні заняття №6, 7

Тема 5. Закони розподілу та числові характеристики випадкових величин

Мета заняття: Закріпити теоретичні знання і набути практичні навички використання основних законів розподілу і розрахунку числових характеристик випадкових величин в ході розв’язання практичних задач.

Обладнання: 1. Методичні рекомендації і завдання до практичних занять; 2. Мікрокалькулятори.

План заняття

1. Основні теоретичні відомості з теми заняття.

2. Розв’язування задач.

3. Підведення підсумків заняття.

Методичні рекомендації

Основними законами розподілу для ДВВ є:

1) біноміальний – випадкова величина приймає значення 0, 1, ..., n з наступними ймовірностями .

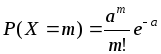2) розподіл Пуассона – випадкова величина приймає злічену множину значень . з ймовірностями.Цей розподіл використовують у задачах статистичного контролю якості, в теорії надійності, теорії масового обслуговування, для обчислення кількості вимог на виплату страхових сум за рік, кількості дефектів однакових виробів.

Основними законами розподілу для НВВ є:

1) рівномірний розподіл:

2) експоненціальний розподіл: 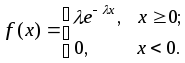, де > 0 - параметр.

3) нормальний розподіл: 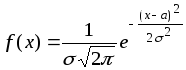, x∈ℝ.

Параметр а – математичне сподівання , – середнє квадратичне відхилення.

Якщо випадкова величина розподілена за нормальним законом, то . Справедлива також формула.

4) розподіл . Розподілом (“хі квадрат”) зk ступенями свободи називається розподіл випадкової величини , де - незалежні однаково розподілені випадкові величини з нормованим розподіломN(0, 1). Щільність розподілу випадкової величини дорівнює

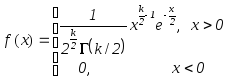, де 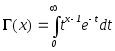– так звана гамма-функція.

5) розподіл Стьюдента. Розподілом Стьюдента (або t-розподілом) з ступенями свободи називається розподіл випадкової величини 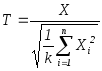, деX, X_i – незалежні однаково розподілені випадкові величини з розподілом N(0, 1).

До основних числових характеристик, які описують розподіл випадкової величини, належать математичне сподівання, дисперсія, середнє квадратичне відхилення, мода, медіана.

Математичним сподіванням випадкової величини X, визначеною на дискретному просторі, називається величина

.

Якщо простір є неперервним, то математичним сподіванням неперервної випадкової величини X називається величина

.

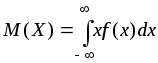Дисперсією випадкової величини X називається математичне сподівання квадрата відхилення випадкової величини від її математичного сподівання

,

або D(X)=M(X²)-M²(X).

Середнім квадратичним відхиленням випадкової величини X називають корінь квадратний із дисперсії:

Для біноміального розподілу ,.

Для розподілу Пуассона ,.

Для нормального розподілу ,.

Задачі для розв’язання

1. За заданим законом розподілу ймовірностей

обчислити M(X), D(X), (X).

2. Нехай Х – число гербів, що випали при підкиданні двох симетричних монет. Записати закон розподілу випадкової величини Х. Обчислити M(X), D(X)

3. Задано функцію розподілу ймовірностей випадкової величини Х:

.

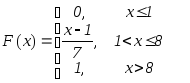Знайти M(x). Обчислити Р(2<Х<3,5).

4. Знайти математичне сподівання і дисперсію кількості очок, що з’являться в результаті одного підкидання грального кубика.

5. За заданою щільністю ймовірностей

f(x)=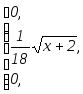

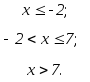
обчислити M(x).

6. Графік щільності розподілу імовірності зображено на рисунку.

f(x)

1/3

-2 -1 1 2 3 4

Знайти аналітичний вираз щільності розподілу. Обчислити D(X), (X), Мо, Ме.

7. Знайти математичне сподівання випадкової величини з а) біноміальним розподілом, б) розподілом Пуассона, в) рівномірним розподілом.

8. По мішені проведено 9 пострілів. Імовірність влучення у мішень при кожному пострілі дорівнює 0,7. Знайти математичне сподівання і дисперсію числа влучень.

9. Випадкова величина Х розподілена за нормальним законом з математичним сподіванням 40 і дисперсією 200. Обчислити ймовірність влучення Х в інтервал (30,80).

10. Випадкова величина Т – час роботи приладу має показниковий розподіл. Визначити ймовірність того, що час роботи приладу буде не менше 600 годин, якщо середній час роботи становить 400 годин.

Т е с т и

Варіант №1

1. Знайти математичне сподівання числа очок, які можуть з’явитися при підкиданні грального кубика.

а) 3; б) 1/2; в) 7/2; г) 5/2.

2. Випадкова величина Х задана щільністю імовірності:

Визначити дисперсію величини Х.

а) 1/2; б) 2/3; в) 2/9; г) -2/3

3. Випадкова величина розподілена за показниковим законом з параметром 5. Знайти М( Х ) і D( Х ).

а) М( Х )=5 D( Х )=25; б) М( Х )=0,2 D( Х )=0,2;

в) М( Х )=0,2 D( Х )=0,04; г) М( Х )=0,5 D( Х )=0,5.

4. Який з наступних законів розподілу не відноситься до розподілу дискретних випадкових величин?

а) рівномірний;

б) пуассонівський;

в) геометричний;

г) біноміальний.

5. Випадкова величина Х розподілена за законом . Знайти М(Х ) і ( Х ).

а) М( Х )=2 ( Х )=2; б) М( Х )=-1 ( Х )=2;

в) М( Х )=8 ( Х )=4; г) М( Х )=-2 ( Х )=1.

Варіант №2

1. Знайти дисперсію випадкової величини Х, що задана законом

Х	-5	0	4	5
Р	1/8	1/2	1/4	1/8

а) 86/8; б) –74/8; в) 1; г) 74/8.

2. Задана інтегральна функ­ція

F(x)=;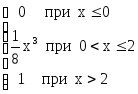

M(X) дорівнює: а) 1/2; б) 7/8; в) 7/8; г) 3/2.

3. Випадкова величина розподілена рівномірно в інтервалі (-2;2).

Знайти М( Х ) і D( Х ).

а) М( Х )=0 D( Х )=1,33; б) немає вірної відповіді;

в) М( Х )=0 D( Х )=4; г) М( Х )=0,5 D( Х )=1,25.

4. За яких умов ймовірність влучення випадкової величини Х в інтервал (c, d) знаходять за формулою: .

а) Х має рівномірний розподіл;

б) Х має показниковий розподіл;

в) Х має нормальний розподіл;

г) Х має біноміальний розподіл.

5. Випадкова величина Х має показників розподіл з параметром 3. Знайти імовірність того, що Х потрапить в інтервал (0,13; 0,7).

а) 0,555; б) 1; в) 0,34 г) 0,445.