Література

Обов’язкова: [1]. Додаткова:[1], [4], [7].

Практичне заняття №4

Тема 3. Схема незалежних випробувань

Мета заняття: Закріпити теоретичні знання і набути практичні навички використання формул для розрахунку ймовірностей у повторних незалежних випробуваннях в ході розв’язання практичних задач.

Обладнання: 1. Методичні рекомендації і завдання до практичних занять; 2. Мікрокалькулятори.

План заняття

1. Основні теоретичні відомості з теми заняття.

2. Розв’язування задач.

3. Підведення підсумків заняття

Методичні рекомендації

Якщо кожний експеримент має лише два несумісні наслідки зі сталими ймовірностями р і q, то їх називають експериментами за схемою Бернуллі. У кожному експерименті випадкова подія з імовірністю р відбувається, а з імовірністю q — не відбувається, тобто р + q = 1.

Імовірність того, що в результаті п незалежних експериментів за схемою Бернуллі подія А з'явиться т раз, подається у вигляді:

.

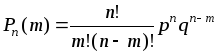Найімовірнішим числом (модою) появи випадкової події А в результаті п незалежних експериментів за схемою Бернуллі називається таке число т₀, для якого ймовірність перевищує або в усякому разі є не меншою за ймовірність кожного з решти можливих наслідків експериментів.

Якщо р≠0 і р≠1, то число т₀ можна знайти з нерівності:

.

Локальна теорема. Якщо ймовірність появи випадкової події в кожному з п незалежних експериментів є величиною сталою і дорівнює р ,то для великих значень п і т імовірність того, що випадкова подія А настане т раз, подається такою асимптотичною формулою:

,

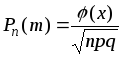де 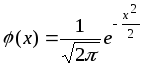–функція Гауса, .

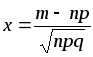Інтегральна теорема. Якщо ймовірність появи випадкової події в кожному з п незалежних експериментів є величиною сталою і дорівнює р, то для великих значень п імовірність появи випадкової події від до раз обчислюється за такою асимптотичною формулою:

,

де , .

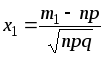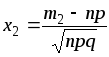Точність асимптотичної формули Лапласа для великих значень знижується з наближенням р до нуля. Тому при ,за умовиnр=а=сonst імовірність появи випадкової події m раз обчислюється за асимптотичною формулою Пуассона:

.

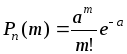Задачі для розв’язання

1. Імовірність влучення стрілком у десятку дорівнює 0,6. Чому дорівнює імовірність того, що при 8 пострілах буде 6 влучень у десятку?

2. Гральний кубик підкидають 7 разів. Знайти імовірність того, що три рази з'явиться число очок, кратне 3.

3. У кожному із семи ящиків міститься по 6 стандартних і 4 браковані однотипні деталі. Навмання з кожного ящика беруть по одній деталі. Обчислити ймовірність того, що серед семи взятих деталей стандартних буде: 1) 3; 2) не менш як 3; 3) не більш як 3.

4. На автобазі є 12 пасажирських автобусів імовірність того, що на маршрутну лінію вийде автобус, у середньому дорівнює 0,85. Знайти ймовірність того, що автобаза працюватиме в нормальному режимі, якщо для цього потрібно, аби на маршрутну лінію виїхало не менш як 9 автобусів.

5. У разі ввімкнення запалювання мотор автомобіля почне працювати з імовірністю 0,99. Яка ймовірність того, що: 1) мотор почне працювати при двох увімкненнях запалювання; 2) не більш як двох.

6. Імовірність появи успіху в кожному іспиті дорівнює 0,25. Знайти імовірність того, що при 300 іспитах успіх наступить рівно 75 разів.

7. У партії однотипних деталей стандартні становить 82%. Навмання з партії беруть 400 деталей. Яка ймовірність того, що серед них стандартних буде: 1) 355; 2) від 355 до 300 Знайти найімовірніше число появи стандартних деталей то і обчислити відповідну ймовірність.

8. В урні 100 білих і 80 чорних куль. З урни витягують n куль (з поверненням). Найімовірніше число появи білої кулі дорівнює 11. Знайти n.

9. Відомо, що серед виробів заводу стандартні деталі становлять у середньому 85%. Скільки необхідно взяти цих деталей, щоб m_o =65?

10. Телефонна станція обслуговує 1000 абонентів. Імовірність того, що протягом години абонент розмовлятиме по телефону, дорівнює в середньому 0,002. Яка ймовірність того, що протягом години одночасно розмовлятимуть по телефону: 1) 5 абонентів; 2) не більш як 5?

Т е с т и

Варіант №1

1. Ймовірність того, що в n незалежних випробуваннях подія А настане не менше m₁ і не більше m₂ раз, можна обчислити за

а) формулою повної ймовірності;

б) теоремою добутку ймовірностей;

в) формулою Пуассона;

г) інтегральною теоремою Муавра-Лапласа.

2. Імовірність влучення стрілком у мішень при одному пострілі дорівнює 0,75. Знайти ймовірність того, що при 10 пострілах буде 8 влучень?

а) 0,209; б) 0,282; в) 0,35; г) 0,273.

3. У партії однотипних деталей стандартні становлять 82%. Навмання з партії беруть 400 деталей. Знайти найімовірніше число появи стандартних деталей.

а) 320; б) 328; в) 57; г) 206.

4. Гральний кубик підкидають 800 разів. Яка ймовірність того, що кількість очок, кратна трьом, з’явиться не менше 260 та не більше 274 разів?

а) 0,4211; б) 0,1914; в) 0,4003; г) 0,2088.

5. Прилад складено з 10 блоків, надійність кожного з яких 0,8.

Блоки можуть виходити з ладу незалежно один від одного. Знайти ймовірність того, що відмовлять 2 блоки.

а) 0,302; б) 0,892; в) 0,0000737; г) 0,006.

Варіант №2

1. Число m₀ появи події в серії з n випробувань називається найімовірнішим числом, якщо

а) це число є найбільшим серед всіх інших;

б) воно співпадає з числом випробувань n;

в) воно відповідає найбільшій ймовірності в даній серії випробувань;

г) подія, яка відповідає цьому числу є вірогідною.

2. Імовірність влучення стрілком у десятку дорівнює 0,6. Чому дорівнює імовірність того, що при 8 пострілах буде 6 влучень у десятку?

а) 0,209; б) 0,418; в) 0,2; г) 0,041.

3. Засівний фонд має 92% насіння першого сорту. Навмання взято 150 насінин. Знайти імовірність того, що серед цих насінин 140 є першого сорту.

а) 0,123; б) 0,3; в) 0,8; г) 0,1004.

4. Скільки разів треба кинути гральний кубик, щоб найімовірніше число появи трійки дорівнювало 55? а) 40; б) 100; в) 330; г) 410.

5. Імовірність виготовлення виробу відмінної якості дорівнює 0,9. Виготовлено 50 виробів. Чому дорівнює найімовірніше число виробів відмінної якості?

а) 45; б) 47; в) 50; г) 10.