2. Закон розподілу та числові характеристики функції дискретного випадкового аргументу

Нехай , аргументX - дискретна випадкова величина. У цьому випадку Y також дискретна випадкова величина із відповідними значеннями.

Математичне сподівання, дисперсію та середнє квадратичне відхилення функції Y обчислюють за формулами:

, (7.1)

, (7.2)

. (7.3)

3. Закон розподілу та числові характеристики функції неперервного випадкового аргументу

Нехай X — неперервна випадкова величина, закон розподілу якої заданий диференціальною функцією розподілу (щільністю ймовірностей) ; випадкова величина.

Якщо - диференційовна функція, монотонна на усьому проміжку можливих значень X, то щільність розподілу функції

визначають так

.

де - функція, обернена по відношенню до функції .

Питання для самоконтролю

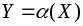1. Як обчислити щільність ймовірностей випадкової величини , якщо, де — монотонна функція, і відомий закон розподілу випадкової величиниX.

2. Як обчислити , якщо, де — немонотонна функція і відомий закон розподілу випадкової величини X?

3. Числові характеристики функції дискретного випадкового аргументу.

4. Числові характеристики функції неперервного випадкового аргументу.

Література

Обов’язкова: [1]. Додаткова:[1], [4], [7].

Тема 8. Граничні теореми теорії ймовірностей

Мета роботи: розібрати нерівність Чебишова, теорему Чебишова, центральну граничну теорему теорії ймовірностей, з’ясувати умови їх застосування.

План вивчення теми

1. Нерівність Чебишова.

2. Теорема Чебишова.

3. Центральна гранична теорема теорії ймовірностей.

Методичні рекомендації до самостійної роботи

Граничні теореми теорії ймовірностей встановлюють відповідність між теоретичними та дослідними характеристиками випадкових величин або випадкових подій при великій кількості випробувань. Граничні теореми описують також граничні закони розподілу.

Граничні теореми, які встановлюють відповідність між теоретичними та дослідними характеристиками випадкових подій, об'єднують загальною назвою - закону великих чисел.

1. Нерівність Чебишова

Якщо випадкова величина має обмежені і, то

. (8.1)

2. Теорема Чебишова

Нехай задано незалежних випадкових величин(, обмеженіі(), тоді

. (8.2)

3. Центральна гранична теорема теорії ймовірностей

Нехай задано незалежних випадкових величин(, кожна із яких має один і той самий закон розподілу ймовірностей із,і при цьому існує за абсолютною величиною початковий момент третього порядку, тоді зі зростанням числазакон розподілунаближається до нормального.

Питання для самоконтролю

1. Як сформулювати в загальному вигляді закон великих чисел?

2. Сформулювати нерівність Чебишова.

3. Сформулювати умови, які мають виконуватися для нерівності Чебишова.

4. Де використовується нерівність Чебишова.

5. Сформулювати теорему Чебишова.

6. Сформулювати центральну граничну теорему.

Література

Обов’язкова: [1]. Додаткова:[1], [4], [7].

Тема 9. Елементи теорії випадкових процесів і теорії масового обслуговування

Мета роботи: розібрати поняття випадкового, Марковського процесів, процесу народження і загибелі.

План вивчення теми

1. Випадкові процеси.

2. Марковські випадкові процеси. Ланцюги Маркова.

3. Процес народження і загибелі.

4. Елементи теорії масового обслуговування.

Методичні рекомендації до самостійної роботи

1. Випадкові процеси

Теорія випадкових процесів є математичною наукою, що вивчає закономірності випадкових подій у їх динаміці. Ця теорія (за іншою термінологією — теорія випадкових функцій) вивчає процеси, розвиток яких наперед точно неможливо передбачити. Така невизначеність (непередбачуваність) зумовлена дією випадкових факторів на розвиток процесу.

Математичною моделлю випадкового процесу є певна функція від дійсного аргументу, значення якої при кожному фіксованомує випадковою величиною. Саме поняття випадкового процесу (випадкової функції) є узагальнюючим поняттям випадкової величини.

Отже, випадковим процесом називають такий процес, коли при будь-якому можливому значеннівипадкова функціяутворює випадкову величину.

При ми дістанемо випадкову величину, яку називають перерізом випадкового процесу. Чим більше перерізів буде розглянуто, тим детальніше уявлення ми будемо мати про випадковий процес.

Випадкові процеси можна класифікувати за тими чи іншими ознаками.

Елементарною класифікацією випадкових процесів є класифікація за ознаками часу та стану. Випадковий процес називають процесом із дискретною змінною часу, якщо система, в якій він здійснюється, може змінювати свій стан тільки в моменти часу кількість яких є обмеженою, або зліченною.