1.2. Мода та медіана випадкової величини

Модою (Мо) дискретної випадкової величини X називають те її можливе значення, якому відповідає найбільша ймовірність появи.

Модою для неперервної випадкової величини X називають те її можливе значення, якому відповідає максимальне значення щільності ймовірності:

.

Якщо випадкова величина має одну моду, то такий розподіл ймовірностей називають одномодальним; якщо розподіл має дві моди — двомодальним і т. ін. Існують і такі розподіли, які не мають моди. їх називають антимодальними.

Медіаною (Ме) неперервної випадкової величини X називають те її значення, для якого виконується рівність:

1.3. Дисперсія та середнє квадратичне відхилення

Математичне сподівання не дає достатньо повної інформації про випадкову величину, оскільки одному й тому самому значенню М(Х) може відповідати безліч випадкових величин, які будуть різнитися не лише можливими значеннями, а й характером розподілу і самою природою можливих значень.

Математичне сподівання називають центром розсіювання. Для вимірювання розсіювання вводиться числова характеристика, яку називають дисперсією.

Для визначення дисперсії розглядається відхилення випадкової величини X від свого математичного сподівання .

Дисперсією випадкової величини X називається математичне сподівання квадрата відхилення цієї величини

(5.3)

Для дискретної випадкової величини X дисперсія:

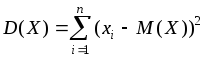(5.4)

для неперервної:

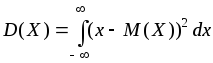(5.5)

Властивості дисперсії:

1. Якщо С – стала величина, то

.

2. D(СХ) =.

3. Якщо А і В є сталими величинами, то

Якщо випадкова величина виміряна в деяких одиницях, то дисперсія вимірюватиметься в цих самих одиницях, але в квадраті.

Тому доцільно мати числову характеристику такої самої вимірності, як і випадкова величина. Такою числовою характеристикою є середнє квадратичне відхилення.

Середнім квадратичним відхиленням випадкової величини X називають корінь квадратний із дисперсії:

(5.6)

1.4. Початкові та центральні моменти

Узагальненими числовими характеристиками випадкових величин є початкові та центральні моменти.

Початковим моментом -го порядку випадкової величини X називають математичне сподівання величини :

.

Для ДВВ: ,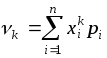

для НВВ: .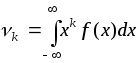

Центральним моментом -го порядкувипадкової величини X називають математичне сподівання від :

.

1.5. Асиметрія і ексцес

Третій центральний момент характеризує асиметрію закону розподілу випадкової величини. Якщо , то випадкова величинаX симетрично розподілена відносно М(Х). Оскільки має розмірність випадкової величини в кубі, то вводять безрозмірну величину — коефіцієнт асиметрії:

.

Центральний момент четвертого порядку використовується для визначення ексцесу, що характеризує плосковершинність, або гостровершинність щільності ймовірності . Ексцес обчислюється за формулою

.

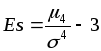2. Біноміальний закон розподілу

Цей закон має вигляд

, (5.7)

і використовується у схемі Бернуллі, тобто у випадку незалежних повторних випробувань, в кожному з яких деяка подія з'являється з ймовірністюр.

Для біноміального розподілу: ,.

2. Закон розподілу Пуассона

ДВВ X приймає злічену множину значень (.) з ймовірностями

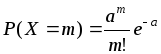. (5.8)

Цей розподіл використовують в задачах статистичного контролю якості, в теорії надійності, теорії масового обслуговування, для обчислення: кількості вимог на виплату страхових сум за рік, кількості дефектів однакових виробів.

Для розподілу Пуассона: ,.

2. Рівномірний розподіл

Означення 1. НВВ X розподілена рівномірно на проміжку , якщо усі її можливі значення належать цьому проміжку і щільність її ймовірностей на цьому проміжку стала, тобто

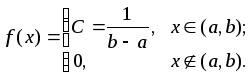(5.9)

Величина сталої С визначається умовою нормування

Цей розподіл задовольняють, наприклад, похибки округлення різноманітних розрахунків.

Числовими характеристиками НВВ X, що розподілена за рівномірним законом, будуть

, .

2. Експоненціальний розподіл

Означення 2. Випадкову величину X називають розподіленою за експоненціальним законом, якщо щільність її ймовірностей має вигляд

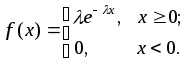(5.10)

де > 0 - параметр.

Експоненціальному розподілу задовольняють: час телефонної розмови, час ремонту техніки, час безвідмовної роботи комп'ютера. Числовими характеристиками експоненціального розподілу будуть

, .

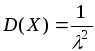2. Нормальний розподіл

Означення 3. Випадкову величину X називають розподіленою нормально, якщо щільність її ймовірностей має вигляд

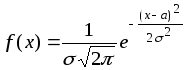. (5.11)

Графік цієї функції називають нормальною кривою або кривою Гауса.

Для цього розподілу:

, .

Отже, математичне сподівання нормального розподілу дорівнює параметру а цього розподілу, а середнє квадратичне відхилення дорівнює параметру .

Зауваження. Якщо випадкова величина Х розподілена за нормальним законом з параметрами а та , то випадкова величинабуде розподілена занормованим нормальним законом і ,.