Область |
|
|
Чертеж |
|
|
Формула |
|
|||
|
|
|
|
|
|
|
|
|
|
|
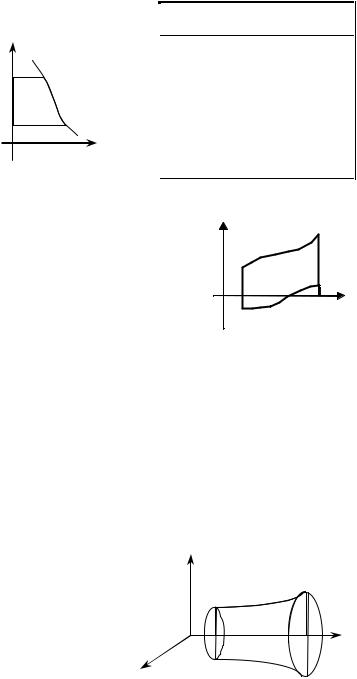
5. Границы D : |
|
y |
|
x = x(y) |
|
|
|
|
|
|
x = 0 , y = a , y =b , x = x(y), |
|
b |
|
|
|
b |
|
|
||
|
|
|
|
|
|
|
|
|||
x( y) ≥ 0 y [a, b] |
|
a |
|
|
|
|
S = ∫x(y)dy |
|
||
|
|
|
x |
|
|
a |
|
|
||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8.1.7. Площадь плоской фигуры |
|
|
|
|
|
|
|
|
|
|
Рассмотрим плоскую фигуру |
D , ограниченную пря- |
y y = y2 (x) |
|
|||||||
мыми x = a , x =b и графиками двух функций y = y1 (x), |
|
a |
|
b |
||||||
y = y2 (x), причем y2 (x)≥ y1 (x) при x [a, b] (рис. 8.1.1). |
|
|
||||||||
0 |
y |
= y1(x) |
x |
|||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
РИС. 8.1.1 |
|
|
Площадь фигуры D при |
любом расположении |
кривых |
y = y1 (x), |
|||||||
y = y2 (x), относительно осей координат находится по формуле |
|
|
|
|||||||
b
S =∫[y2 (x) − y1(x)]dx .
a
8.1.8. Объем тела вращения
1. Пусть криволинейная трапеция D , ограниченная прямыми y = 0 , x = a , x =b и графиком функции y = y(x) (рис. 8.1.2), вращается вокруг
оси Ox . В результате получим тело вращения, объем которого вычисляется по формуле
b
V = π∫y2 (x)dx .
a
y |
y = y(x) |
|
0 |
a |
b x |
|
||
|
РИС. 8.1.2 |
|
(8)
55