2) Что называется неопределенным интегралом от функции f (x)? Каков его геометрический смысл?
3)Какие свойства связывают операции дифференцирования и интегрирования?
4)Сформулируйте свойства линейности неопределенного интеграла.
5)Чему равен интеграл ∫ f (ax + b)dx , если ∫ f (x)dx = F (x)+ C ?
6)Запишите формулу интегрирования по частям.
7)Перечислите виды интегралов, берущихся по частям.
8)По каким правилам разбивается подынтегральное выражение на множители u и dv ?
9)Что называется рациональной дробью? Какая дробь называется правильной, неправильной? Что значит, выделить целую часть?
10)Какие дроби называются простейшими? Какой вид имеет разложение правильной дроби в сумму простейших дробей?
11)Какой вид имеет формула замены переменной в неопределенном интеграле?
Тема 8. Вычисление определенных интегралов. Приложения определенного интеграла. Исследование сходимости несобственных интегралов
8.1. Вопросы для самостоятельного изучения |
|
|
8.1.1. Определение определенного интеграла |
|
|
Дана функция y = f (x) на отрезке [a, b]. Отрезок [a, b] |
разобьем произ- |
|
вольно на n |
частей точками a = x0 < x1 < x2 < ... < xn = b |
и обозначим |
xk = xk − xk−1, |
k =1, 2, ... , n . |
|
Выберем произвольно точки ξk [xk−1, xk ] и найдем значения функции f (ξk ) для k =1, 2, ... , n .
Сумма
n
∑ f (ξk ) xk
k=1
называется интегральной суммой. Она зависит от способа разбиения отрезка
[a, b] на части и выбора точек ξk .
Если существует конечный предел последовательности интегральных
сумм при max xk →0 , не зависящий от способа разбиения отрезка [a, b] на
51
части и от выбора точек ξk , то этот предел называется определенным инте-
гралом от функции f (x) на отрезке [a, b] и обозначается
b
∫ f (x)dx .
Следовательно,
b
∫ f (x)dx =
a
a |
|
|
|
|
n |
maxlimx |
→0 |
∑ f (ξk ) xk . |
k |
|
k=1 |
8.1.2. Свойства определенного интеграла:
1. Свойства линейности:
b |
b |
b |
∫[f1(x) + f2 (x)]dx = ∫ f1(x)dx + ∫ f2 (x)dx ; |
||
a |
a |
a |
b |
|
b |
∫C f (x)dx = C∫ f (x)dx . |
||
a |
|
a |
2. Свойство аддитивности: для любых чисел a, b, c имеем
b |
c |
b |
∫ f (x)dx = ∫ f (x)dx + ∫ f (x)dx .
a |
a |
c |
3. Интегрирование неравенств: если |
f (x)≤ q(x), x [a, b], то |
|
b b
∫ f (x)dx ≤ ∫q(x)dx .
aa
4.Оценка интеграла: если m, M – наименьшее и наибольшее значения
функции f (x) на отрезке [a, b], то
b
m(b − a)≤ ∫ f (x)dx ≤ M (b − a).
a
5. Теорема о среднем: если функция f (x) непрерывна на [a, b], то су-
b
ществует такая точка c [a, b], что ∫ f (x)dx = f (c)(b − a). Значение
a
52
на отрезке [a, b].
8.1.3. Вычисление определенного интеграла, физические приложения определенного интеграла
Формула Ньютона-Лейбница: если F (x) – первообразная непрерывной функции f (x), то справедлива формула
b |
|
b |
|
|
|
|
|
||
∫ f (x)dx = F (x) |
|
= F (b)− F (a). |
(5) |
|
a |
|
a |
|
|
8.1.4. Интегрирование по частям в определенном интеграле |
|
|||
Если u(x), v(x) – дифференцируемые функции на отрезке [a, b], то име- |
||||
ет место формула интегрирования по частям |
|
|||
b |
|
|
b |
|
∫u dv = uv b |
− ∫vdu . |
(6) |
||
aa a
8.1.5.Формула замены переменной в определенном интеграле
b
Рассмотрим определенный интеграл ∫ f (x)dx . Пусть x = x(t) – диффе-
a
ренцируемая функция, удовлетворяющая условиям: a = x(α), b = x(β).
Тогда в определенном интеграле можно перейти к новой переменной t согласно формуле
|
|
x = x(t) |
|
|
|
|
b |
|
′ |
|
β |
′ |
|
|
dx = x (t)dt |
|
= ∫ |
(7) |
||
∫ f (x)dx = |
|
|
f (x(t))x (t)dt. |
|||
a |
x = a t = α |
α |
|
|
||
|
|
|
|
|
|
|
x =b t =β
Эта формула называется формулой замены переменной в определенном интеграле, а функция x = x(t) – подстановкой.
53
8.1.6. Приложения определенного интеграла
Криволинейной трапецией называется плоская фигура, ограниченная осью Ox (уравнение y = 0 ), вертикальными прямыми x = a, x = b и графиком функции f (x).
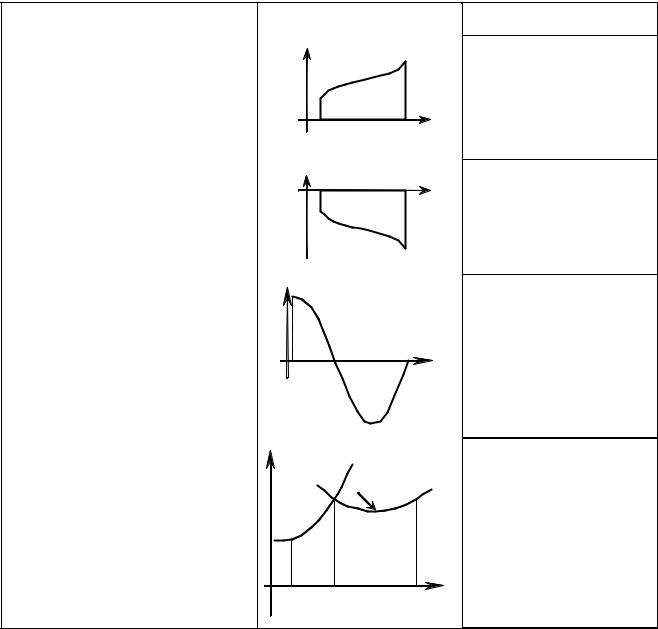
ТАБЛИЦА 8.1.1. ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ ПЛОЩАДИ КРИВОЛИНЕЙНОЙ
ТРАПЕЦИИ
Область |
|
|
|
|
|
Чертеж |
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Границы D : y = 0 , |
x = a , |
|
y |
|
y = y(x) |
|
|
||
x = b , y = y(x), y(x)≥ 0 при |
|
|
|
|
|
|
|
|
|
x [a,b]. |
|
|
0 |
a |
|
b |
x |
||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
2. Границы D : y = 0 , |
x = a , |
|
y |
a |
|
b |
|
||
x = b , y = y(x), y(x)≤ 0 при |
|
0 |
|
|
|
|
x |
||
x [a,b]. |
|
|
|
y = y(x) |
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
3. Границы D : y = 0 , |
x = a , |
|
y |
|
|
|
|
|
|
x = b , y = y(x); y(x)≥ 0 при |
|
|
|
|
y = y(x) |
|
|
||
|
|
+ |
|
|
|
||||
x [a,c], y(x)≤ 0 при |
|
|
|
|
с |
|
|
|
|
|
|
a |
|
− |
b |
x |
|||
|
|
|
|
|
|||||
x [c,b]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Границы D : y = 0 , |
x = a , |
y |
|
|
|
|
|
|
|
x = b , y = y (x) при x [a,c], |
y |
= y1 |
(x) |
y = y2 |
(x) |
||||
|
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|
|
y = y2 (x) при x [a,b].
0 |
b x |
a с |
Формула
b
S = ∫y(x)dx
a
b
S = −∫y(x)dx
a
c b
S =∫y(x)dx −∫y(x)dx
a c
c |
b |
S =∫y1(x)dx +∫y2 (x)dx |
|
a |
c |
54