
МатАн_ЛинАлг_080100 / ЛА_экз_1курс_экономика_заочн
.docF1:Линейная алгебра 1 курс экзамен экономика заочное
F2: Поташев А.В., Поташева Е.В.
F3:
F4: Дидактическая единица; Тема
V1: Линейная алгебра
V2: Формулы вычисления определителей
I:
S:
Формула вычисления определителя третьего
порядка
 содержит следующие произведения: …
содержит следующие произведения: …
+:
![]()
-:
![]()
-:
![]()
+:
![]()
I:
S:
Формула вычисления определителя третьего
порядка
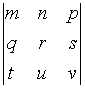 содержит следующие произведения: …
содержит следующие произведения: …
+:
![]()
-:
![]()
+:
![]()
-:![]()
I:
S:
Формула вычисления определителя третьего
порядка
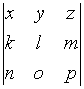 содержит
следующие произведения: …
содержит
следующие произведения: …
+:
![]()
-:
![]()
-:
![]()
+:
![]()
I:
S:
Формула вычисления определителя третьего
порядка
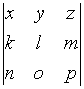 содержит
следующие произведения: …
содержит
следующие произведения: …
-:
![]()
-:
![]()
+:
![]()
+:
![]()
I:
S:
Формула вычисления определителя третьего
порядка
 содержит
следующие произведения: …
содержит
следующие произведения: …
-:
![]()
+:
![]()
+:
![]()
-:
![]()
V2: Определители второго порядка
I:
S: Установите соответствие между матрицей и ее определителем.
L1:

L2:

L3:

R4: 480
R5: - 20
R3: 0
R1: - 7
R2: - 40
I:
S: Установите соответствие между матрицей и ее определителем.
L1:
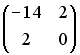
L2:
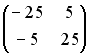
L3:
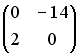
R1: - 4
R2: - 600
R3: 28
R4: - 28
R5: 0
I:
S: Установите соответствие между матрицей и ее определителем.
L1:
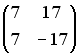
L2:

L3:

R1: - 238
R4: - 49
R2: 49
R5: 119
R3: - 119
I:
S: Установите соответствие между матрицей и ее определителем.
L1:
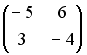
L2:
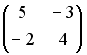
L3:
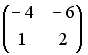
R5: 12
R2: 14
R3: - 2
R4: - 14
R1: 2
I:
S: Установите соответствие между матрицей и ее определителем.
L1:
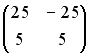
L2:
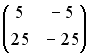
L3:
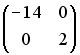
R1: 250
R2: 0
R4: - 125
R3: - 28
R5: 28
I:
S:
Установите соответствие между
![]() и
значениями определителей
и
значениями определителей
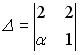 .
.
L1:
![]()
L2:
![]()
L3:
![]()
L4:
![]()
R6:
![]()
R5:
![]()
R1:
![]()
R2:
![]()
R4:
![]()
R3:
![]()
I:
S:
Установите соответствие между
![]() и
значениями определителей
и
значениями определителей
 .
.
L1:
![]()
L2:
![]()
L3:
![]()
L4:
![]()
R2:
![]()
R3:
![]()
R4:
![]()
R1:
![]()
R5:
![]()
R6:
![]()
I:
S:
Установите соответствие между
![]() и
значениями определителей
и
значениями определителей
 .
.
L1:
![]()
L2:
![]()
L3:
![]()
L4:
![]()
R2: Δ= -8
R1:
![]()
R5:
![]()
R4:
![]()
R3:
![]()
R6:
![]()
I:
S:
Установите соответствие между
![]() и
значениями определителей
и
значениями определителей
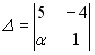 .
.
L1:
![]()
L2:
![]()
L3:
![]()
L4:
![]()
R3:
![]()
R6:
![]()
R5:
![]()
R1:
![]()
R4:
![]()
R2:
![]()
I:
S:
Установите соответствие между
![]() и
значениями определителей
и
значениями определителей
 .
.
L1:
![]()
L2:
![]()
L3:
![]()
L4:
![]()
R6:
![]()
R1:
![]()
R3:
![]()
R4:
![]()
R5:
![]()
R2:
![]()
V2: Определители третьего порядка
I:
S:
Определитель
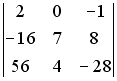 равен
…
равен
…
+: 0
I:
S:
Определитель
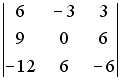 равен
…
равен
…
+: 0
I:
S:
Определитель
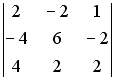 равен
…
равен
…
+: 0
V2: Линейные операции над матрицами
I:
S:
Если
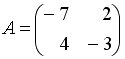 ,
то матрица
,
то матрица
![]() имеет
вид...
имеет
вид...
-:

+:

-:
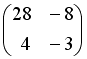
-:

I:
S:
Даны матрицы
 и
и
 .
Тогда
.
Тогда
![]() равно
…
равно
…
-:
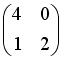
-:
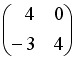
-:
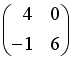
+:

I:
S:
Даны матрицы
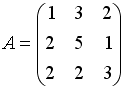 ,
,
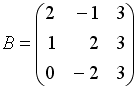 .
Тогда матрица
.
Тогда матрица
![]() равна…
равна…
-:
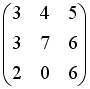
-:

+:
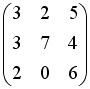
-:

I:
S:
Даны матрицы
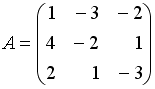 ,
,
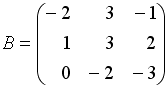 .
Тогда матрица
.
Тогда матрица
![]() равна
…
равна
…
-:

-:

-:
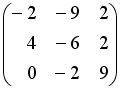
+:

I:
S:
Даны матрицы
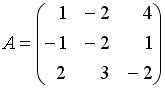 ,
,
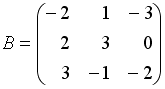 .
Тогда матрица
.
Тогда матрица
![]() равна
…
равна
…
-:

-:

+:
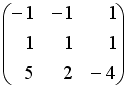
-:

I:
S:
Вычислите сумму элементов первого
столбца матрицы
![]() ,
если
,
если
 ,
,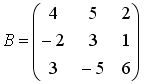
+: -7
I:
S:
Вычислите сумму элементов первого
столбца матрицы
![]() ,
если
,
если
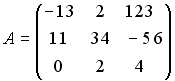 ,
,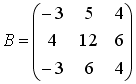
+: 2
I:
S:
Вычислите сумму элементов первого
столбца матрицы
![]() ,
если
,
если
 ,
,
+: -16
I:
S:
Вычислите сумму элементов первого
столбца матрицы
![]() ,
если
,
если
 ,
,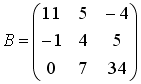
+: -34
I:
S:
Вычислите сумму элементов первого
столбца матрицы
![]() ,
если
,
если
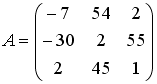 ,
,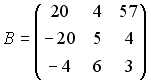
+: -58
I:
S:
Если
 и
и
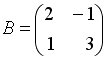 ,
то матрица
,
то матрица
![]() имеет
вид…
имеет
вид…
-:
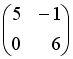
+:

-:

-:
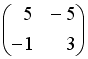
I:
S:
Даны матрицы
 и
и
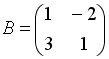 .
Тогда решением матричного уравнения
.
Тогда решением матричного уравнения
![]() является
матрица …
является
матрица …
-:
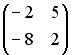
+:

-:

-:
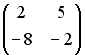
I:
S:
Даны матрицы
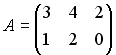 и
и
 .
Тогда матрица
.
Тогда матрица
![]() ,
являющаяся решением уравнения
,
являющаяся решением уравнения
![]() ,
равна …
,
равна …
-:

-:

-:
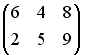
+:

V2: Умножение матриц
I:
S: Операция произведения матриц правильно определена для матричного умножения вида …
+:

-:
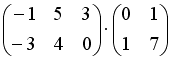
+: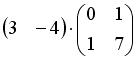
+: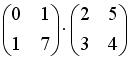
-: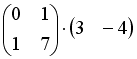
I:
S: Операция произведения матриц правильно определена для матричного умножения вида …
-:
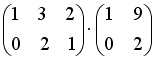
+: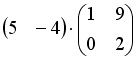
-:
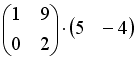
+:
+:
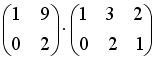
I:
S:
Даны матрицы
![]() размерности
размерности
![]() и
и
![]() размерности
размерности
![]() .
Произведение
.
Произведение
![]() существует
и имеет размерность…
существует
и имеет размерность…
-:
![]()
-:
![]()
+:
![]()
-:
![]()
I:
S:
Даны матрицы
![]() размерности
размерности
![]() и
и
![]() размерности
размерности
![]() .
Произведение
.
Произведение
![]() существует
и имеет размерность…
существует
и имеет размерность…
-:
![]()
-:
![]()
-:
![]()
+:
![]()
I:
S:
Для матриц А и В найдено произведение
![]() ,
причем
,
причем
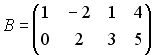 .
Тогда матрица А должна иметь …
.
Тогда матрица А должна иметь …
-: 1 столбец
+: 2 столбца
-: 3 столбца
-: 4 столбца
I:
S:
Даны матрицы
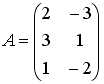 и
и
 .
Тогда матрица
.
Тогда матрица
![]() имеет
размерность …
имеет
размерность …
-:
![]()
+:
![]()
-:
![]()
-:
![]()
I:
S:
Дана матрица 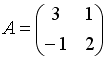 .
Тогда элемент
.
Тогда элемент
![]() матрицы
матрицы
![]() равен
…
равен
…
+: 5
-: - 5
-: - 1
-: 1
I:
S:
Даны матрицы
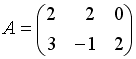 и
и
 .
Сумма элементов матрицы
.
Сумма элементов матрицы
![]() ,
расположенных на ее главной диагонали,
равна …
,
расположенных на ее главной диагонали,
равна …
+: 15
I:
S:
Даны матрицы
 и
и
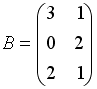 .
Сумма элементов матрицы
.
Сумма элементов матрицы
![]() ,
расположенных на ее главной диагонали,
равна …
,
расположенных на ее главной диагонали,
равна …
+: 9
I:
S:
Даны матрицы
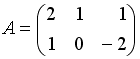 и
и
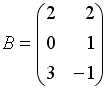 .
Сумма элементов матрицы
.
Сумма элементов матрицы
![]() ,
расположенных на ее главной диагонали,
равна …
,
расположенных на ее главной диагонали,
равна …
+: 11
I:
S:
Даны матрицы
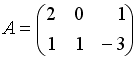 и
и
 .
Сумма элементов матрицы
.
Сумма элементов матрицы
![]() ,
расположенных на ее главной диагонали,
равна …
,
расположенных на ее главной диагонали,
равна …
+: 10
I:
S:
Даны матрицы
 и
и
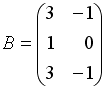 .
Сумма элементов матрицы
.
Сумма элементов матрицы
![]() ,
расположенных на ее главной диагонали,
равна …
,
расположенных на ее главной диагонали,
равна …
+: 16
I:
S:Если
 ,
,
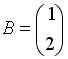 ,
тогда матрица
,
тогда матрица
![]() имеет
вид …
имеет
вид …
-:
![]()
+:
![]()
-:
![]()
-:
![]()
I:
S:
Даны матрицы
 и
и
 .
Тогда произведение
.
Тогда произведение
![]() равно
…
равно
…
-:
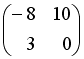
-:

-:
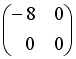
+:

I:
S:
Для матриц А и В найдено произведение
![]() ,
причем
,
причем
 .
Тогда матрицей В может быть матрица …
.
Тогда матрицей В может быть матрица …
-:

-:
![]()
+:
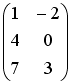
-:
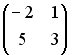
I:
S:
Заданы матрицы
 ,
,
 .
Тогда элемент
.
Тогда элемент
![]() матрицы
матрицы
![]() равен
…
равен
…
+: 3
-: − 11
-: − 7
-: 5
I:
S:
Дана матрица
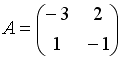 .
Тогда матрица
.
Тогда матрица
![]() имеет
вид …
имеет
вид …
-:

-:
![]()
+:

-:
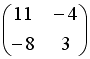
V2: Системы линейных уравнений: метод Крамера
I:
S:
Дана система уравнений
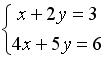 .
Для того, чтобы найти значение переменной
y при решении этой
системы по формулам Крамера, достаточно
вычислить только определители…
.
Для того, чтобы найти значение переменной
y при решении этой
системы по формулам Крамера, достаточно
вычислить только определители…
