МатАн_ЛинАлг_080100 / ЛА_экз_1курс_экономика_заочн

+: и

-: и

-: и

-: ,  и

I:

S: Дана система уравнений 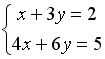. Для того, чтобы найти значение переменной y при решении этой системы по формулам Крамера, достаточно вычислить только определители…

-: ,  и

+: и

-: и

-: и

I:

S: При решении системы линейных уравнений с квадратной матрицей коэффициентов  можно применять формулы Крамера, если

-: один из столбцов матрицы  является линейной комбинацией остальных

+: столбцы матрицы  линейно независимы

+: определитель матрицы  не равен нулю

-: строки матрицы  линейно зависимы

I:

S: При решении системы линейных уравнений с квадратной матрицей коэффициентов  можно применять формулы Крамера, если

+: строки матрицы  линейно независимы

+: определитель матрицы  не равен нулю

-: столбцы матрицы  линейно зависимы

-: одна из строк матрицы  является линейной комбинацией остальных

I:

S: При решении системы линейных уравнений с квадратной матрицей коэффициентов  нельзя применять формулы Крамера, если

-: ни одна из строк матрицы  не является линейной комбинацией остальных

-: столбцы матрицы  линейно независимы

+: строки матрицы  линейно зависимы

+: определитель матрицы  равен нулю

I:

S: При решении системы линейных уравнений с квадратной матрицей коэффициентов  можно применять формулы Крамера, если

+: ни одна из строк матрицы  не является линейной комбинацией остальных

-: определитель матрицы  равен нулю

-: матрица  имеет два пропорциональных столбца

+: ранг матрицы  равен числу ее столбцов

I:

S: При решении системы линейных уравнений с квадратной матрицей коэффициентов  нельзя применять формулы Крамера, если

+: ранг матрицы  не равен числу ее столбцов

-: столбцы матрицы  линейно независимы

-: определитель матрицы  не равен нулю

+: одна из строк матрицы  является линейной комбинацией остальных

I:

S: Система линейных уравнени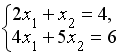й  решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.

L1:

L2:

L3:

R4: 2

R3: - 4

R1: 6

R2: 14

I:

S: Система линейных уравнени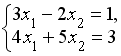й  решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.

L1:

L2:

L3:

R4: - 5

R2: 11

R1: 23

R3: 5

I:

S: Система линейных уравнени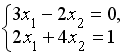й  решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.

L1:

L2:

L3:

R4: - 3

R1: 16

R2: 2

R3: 3

I:

S: Система линейных уравнений  решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.

L1:

L2:

L3:

R4: 3

R1: 27

R2: 13

R3: - 3

I:

S: Система линейных уравнени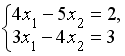й  решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.

L1:

L2:

L3:

R1: - 1

R4: - 6

R3: 6

R2: 7

V2: Системы линейных уравнений: метод Гаусса

I:

S: Укажите систему линейных уравнений, подготовленную для обратного хода метода Гаусса.

-:

-:

-:

+:

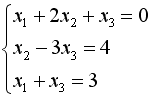
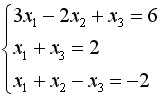
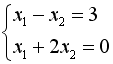
I:

S: Укажите систему линейных уравнений, подготовленную для обратного хода метода Гаусса.

-:

+:

-:

-:

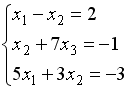
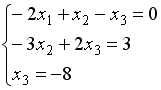
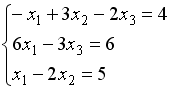
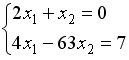
I:

S: Укажите систему линейных уравнений, подготовленную для обратного хода метода Гаусса.

-:

-:

+:

-:

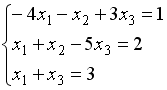
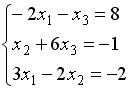
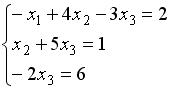
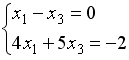
I:

S: Установите соответствие между системой линейных уравнений и ее расширенной матрицей.

L1:

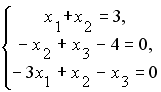
L2:

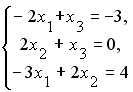
L3:

L4:

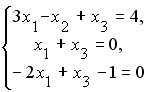
R2:

R5:

R6:

R4:

R1:

R3:

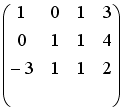
I:

S: Установите соответствие между системой линейных уравнений и ее расширенной матрицей.

L1:

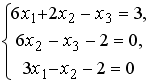
L2:

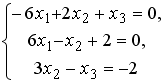
L3:

L4: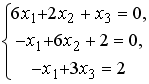

R2:

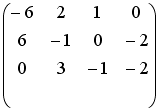
R5:

R1:

R4:

R3:

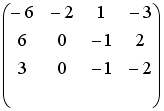
R6:

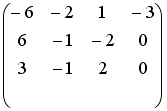
I:

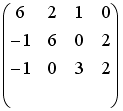
S: Установите соответствие между системой линейных уравнений и ее расширенной матрицей.

L1:

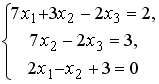
L2:

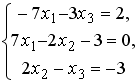
L3:

L4: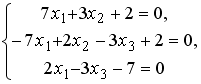

R3:

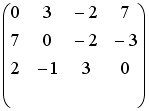
R4: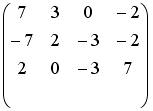

R5:

R1:

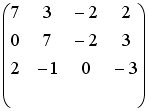
R6:

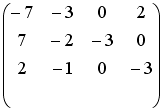
R2:

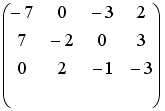
I:

S: Установите соответствие между системой линейных уравнений и ее расширенной матрицей.

L1:

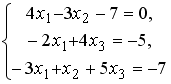
L2:

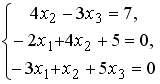
L3:

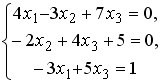
L4:

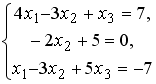
R1:

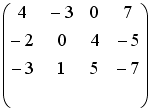
R4:

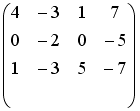
R5:

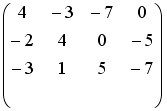
R2:

R3:

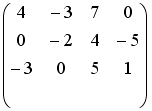
R6:

V1: Аналитическая геометрия

V2: Основные задачи аналитической геометрии на плоскости

I:

S: Даны две смежные вершины квадрата:  и . Тогда площадь этого квадрата равна…

-: 13

-:

-:

+: 29

I:

S: Даны точки  и . Тогда абсцисса середины отрезка  равна…

-: – 3

-: 2

-: – 1

+: 3

I:

S: Даны точки  и . Тогда ордината середины отрезка  равна …

-: 2

+: 1

-: – 1

-: 5

I:

S: Даны точки  и . Тогда ордината середины отрезка  равна …

+: 1

-: – 1

-: 2

-: 4

I:

S: Даны точки  и . Тогда абсцисса середины отрезка  равна …

-: – 9

-: 2

-: – 1

+: – 2

I:

S: Расположите по возрастанию длины сторон треугольника , где ,  и .

3:

2:

1:

I:

S: Расположите по возрастанию длины сторон треугольника , где ,  и .

2:

3:

1:

I:

S: Расположите по возрастанию длины сторон треугольника , где ,  и .

2:

1:

3:

I:

S: Расположите по возрастанию длины сторон треугольника , где ,  и .

2:

3:

1:

I:

S: Расположите по возрастанию длины сторон треугольника , где ,  и .

3:

1:

2:

I:

S: Даны точки ,  и . Установите соответствие между отрезком и его длиной.

L1:

L2:

L3:

R3: 8

R2: 6

R4: 14

R1: 10

R5: 12

I:

S: Даны точки ,  и . Установите соответствие между отрезком и его длиной.

L1:

L2:

L3:

R4: 11

R1: 15

R5: 8

R3: 12

R2: 9

I:

S: Установите соответствие между элементами двух множеств ( - расстояние между точками  А и В)

L1:

L2:

L3:

R1:

R4: 5

R5: 3

R2:

R3: 7

I:

S: Установите соответствие между элементами двух множеств ( - расстояние между точками  А и В)

L1:

L2:

L3:

R1:

R4: 52

R2:

R3: 5

R5: 41

I:

S: Установите соответствие между элементами двух множеств ( - расстояние между точками  А и В)

L1:

L2:

L3:

R3: 6

R4: 45

R5: 22

R1:

R2:

V2: Прямая на плоскости

I:

S: Даны графики прямых: 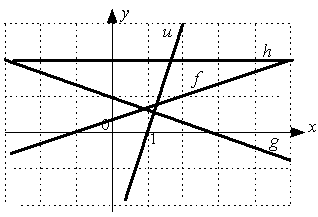Тогда сумма их угловых коэффициентов равна…

+: 3

I:

S: Даны графики прямых : 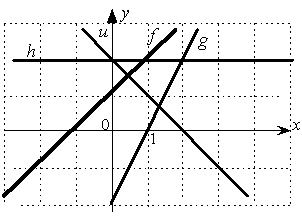Тогда сумма их угловых коэффициентов равна…

+: 2

I:

S: Даны графики прямых : Тогда сумма их угловых коэффициентов равна…

+: 2

I:

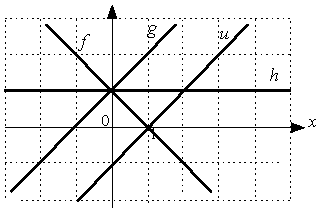S: Даны графики прямых : Тогда сумма их угловых коэффициентов равна…

+: 1

I:

S: Даны графики прямых : 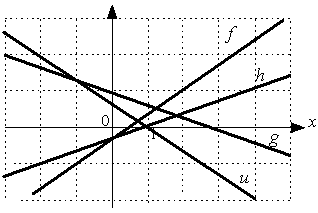Тогда сумма их угловых коэффициентов равна…

+: 0

I:

S:Даны графики прямых : Тогда наименьший угловой коэффициент имеет прямая…

+: f

-: h

-: u

-: g

I:

S: Выберите уравнение прямой, соответствующее данному рисунку.

-:

-:

+:

-:

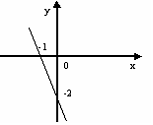
I:

S: Прямая проходит через точки  и . Тогда ее угловой коэффициент равен…

+:

-: 2

-:

-: – 2

I:

S: Расстояние от точки  до прямой   равно…

+: 4

-: 2,4

-: 0,8

-: 5

V2: Кривые второго порядка

I:

S: Установите соответствие между кривой второго порядка и ее уравнением.

L1: Парабола

L2: Эллипс

L3: Гипербола

R2:

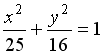
R3:

R4:

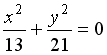
R5:

R1:

I:

S: Укажите соответствие между уравнениями и видами кривых второго порядка.

L1:

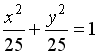
L2:

L3:

R1: окружность

R3: парабола

R2: эллипс

R4: гипербола

I:

S: Укажите соответствие между уравнениями и видами кривых второго порядка.

L1:

L2:

L3:

R4: гипербола

R1: парабола

R2: эллипс

R3: окружность

I:

S: Укажите соответствие между уравнениями и видами кривых второго порядка.