МатАн_ЛинАлг_080100 / МА_экз_1курс_экономика_заочн

F1: Математический анализ 1 курс экзамен экономика заочное

F2: Поташев А.В., Поташева Е.В.

F3: Если при вычислениях получается бесконечность, то в ответе необходимо записать: бесконечность. Дробные числа записываются через косую черту, например, 1/2, 7/12

F4: Дидактическая единица; Тема

V1: Элементы теории множеств

V2: Числовые множества

I:

S: Установить соответствия между списками двух множеств, заданных различным образом:

L1:

L2:

L3:

L4:

R1:

R2:

R3:

R4:

R5:

I:

S: Установить соответствия между списками двух множеств, заданных различным образом:

L1:

L2:

L3:

L4:

R1:

R3:

R5:

R2:

R4: (-1; 5)

I:

S: Установить соответствия между списками двух множеств, заданных различным образом:

L1:

L2:

L3:

L4:

R3:

R2:

R4:

R5:

R1:

I:

S: Установите соответствие между заданными числами и множествами, которым они принадлежат.

L1:

L2:

L3:

L4:

R3:

R1:

R4:

R2:

R5:

I:

S: Установите соответствие между заданными числами и множествами, которым они принадлежат.

L1:

L2:

L3:

L4:

R2:

R1:

R3:

R4:

R5:

V2: Мера плоского множества

I:

S: Мера множества, изображенного на рисунке,

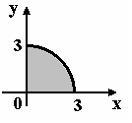
равна…

+:

-:

-:

-:

I:

S: Мера множества, изображенного на рисунке,

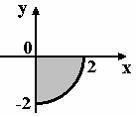
равна…

-:

-:

+:

-:

I:

S: Мера множества, изображенного на рисунке,

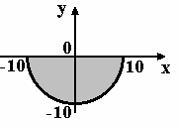
равна…

-:

-:

+:

-:

I:

S: Мера множества, изображенного на рисунке,

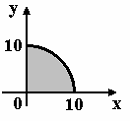
равна…

+:

-:

-:

-:

V1: Понятие функции

V2: Функции: основные понятия и определения.

I:

S: Пусть . Тогда сложная функция  нечетна, если функция  задается формулами…

+:

-:

-:

+:

I:

S: Пусть . Тогда сложная функция  нечетна, если функция  задается формулами…

+:

-:

-:

+:

I:

S: Пусть . Тогда сложная функция  четна, если функция  задается формулами…

+:

-:

-:

+:

I:

S: Пусть . Тогда сложная функция  нечетна, если функция  задается формулами…

+:

-:

-:

+:

I:

S: Пусть . Тогда сложная функция  четна, если функция  задается формулами…

+:

-:

+:

-:

V2: Область определения

I:

S: Областью определения функции является множество точек вида

+:

-:

-:

-:

I:

S: Областью определения функции является множество точек вида

-:

-:

+:

-:

I:

S: Областью определения функции является множество точек вида

-:

+:

-:

-:

I:

S: Областью определения функции является множество точек вида

-:

-:

-:

+ :

I:

S: Областью определения функции является множество точек вида

-:

-:

+ :

-:

I:

S: Областью определения функции является множество точек вида

-:

-:

-:

+:

I:

S: Областью определения функции является множество точек вида

+:

-:

-:

-:

I:

S: Областью определения функции является множество точек вида

+:

-:

-:

-:

I:

S: Областью определения функции является множество точек вида

-:

-:

-:

+:

I:

S: Областью определения функции является множество точек вида

-:

+:

-:

-:

I:

S: Областью определения функции является множество точек вида

-:

-:

+:

-:

V1: Последовательности

V2:Числовые последовательности

I:

S: Установите соответствие между числовой последовательностью и формулой ее общего члена

L1:

L2:

L3:

R1:

R2:

R3:

R4:

R5:

I:

S: Установите соответствие между числовой последовательностью и формулой ее общего члена

L1:

L2:

L3:

R1:

R2:

R3:

R4:

R5:

I:

S: Установите соответствие между числовой последовательностью и формулой ее общего члена

L1:

L2:

L3:

R1:

R2:

R3:

R4:

R5:

I:

S: Установите соответствие между числовой последовательностью и формулой ее общего члена

L1:

L2:

L3:

R1:

R2:

R3:

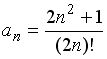
R4:

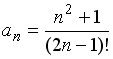
R5:

I:

S: Установите соответствие между числовой последовательностью и формулой ее общего члена

L1:

L2:

L3:

R1:

R2:

R3:

R4:

R5:

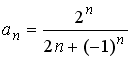
I:

S: Общий член последовательности имеет вид…

+:

-:

-:

-:

I:

S: Общий член последовательности  имеет вид…

+:

-:

-:

-:

I:

S: n+1–ый член числовой последовательности  равен…

-:

+:

-:

-:

I:

S: Последовательность задана рекуррентным соотношением ; .

Тогда четвертый член этой последовательности равен…

-: 31

+: 30

-: 28

-: 32

I:

S: Известны первые три члена числовой последовательности: , , . Тогда формула общего члена этой последовательности имеет вид …

-:

+:

-:

-:

I:

S: Второй член  числовой последовательности  равен

+: 16

I:

S: Второй член  числовой последовательности  равен

+: 8

I:

S: Второй член  числовой последовательности  равен …

+: 7

I:

S: Четвертый член  числовой последовательности  равен …

+: 1

I:

S: Четвертый член  числовой последовательности  равен …

+: 3

I:

S: Общий член последовательности  имеет вид…

+:

-:

-:

-:

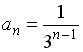
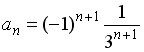
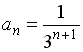
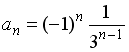
I:

S: -й член числовой последовательности  равен…

-:

+:

-:

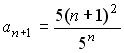
I:

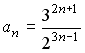S: -й член числовой последовательности  равен…

-:

+:

-:

-:

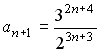
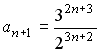
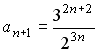
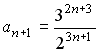
I:

S: Последовательность задана рекуррентным соотношением , . Тогда четвертый член этой последовательности  равен…

-: -5

-: -13

-: -61

+: 3

I:

S: Известны первые три члена числовой последовательности: , , . Тогда формула общего члена этой последовательности имеет вид …

-:

-:

-:

+:

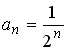
V1: Предел функции

V2: Предел функции на бесконечности

I:

S: Чему равен предел функции ?

+: 1

I:

S: Чему равен предел функции ?

+: бесконечность

I:

S: Чему равен предел функции ?

+: 0

I:

S: Чему равен предел ?

+: 5

I:

S: Чему равен предел функции ?

+: бесконечность

I:

S: Чему равен предел ?

+: 0

I:

S: Чему равен предел ?