
МатАн_ЛинАлг_080100 / ЛА_экз_1курс_экономика_заочн
.docL1:

L2:
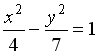
L3:

R2: гипербола
R4: окружность
R1: парабола
R3: эллипс
I:
S: Укажите соответствие между уравнениями и видами кривых второго порядка.
L1:

L2:
![]()
L3:
![]()
R1: окружность
R3: парабола
R2: эллипс
R4: гипербола
I:
S: Укажите соответствие между кривыми второго порядка и их уравнениями:
L1:
![]()
L2:
![]()
L3:
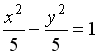
R2: окружность
R3: гипербола
R4: эллипс
R1: парабола
I:
S: Укажите соответствие между кривыми второго порядка и их уравнениями:
L1:
![]()
L2:
![]()
L3:
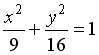
R3: эллипс
R1: парабола
R4: окружность
R2: гипербола
I:
S: Укажите соответствие между кривыми второго порядка и их уравнениями:
L1:
![]()
L2:
![]()
L3:

R1: эллипс
R3: гипербола
R4: окружность
R2: парабола
I:
S: Укажите соответствие между кривыми второго порядка и их уравнениями:
L1:
![]()
L2:
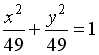
L3:

R4: эллипс
R1: парабола
R3: гипербола
R2: окружность
I:
S: Укажите соответствие между кривыми второго порядка и их уравнениями:
L1:
![]()
L2:
![]()
L3:
![]()
R3: эллипс
R2: парабола
R4: гипербола
R1: окружность
I:
S:
Расстояние между фокусами гиперболы
 равно
…
равно
…
+: 26
I:
S:
Расстояние между фокусами гиперболы
 равно
…
равно
…
+: 40
I:
S:
Расстояние между фокусами гиперболы
 равно
…
равно
…
+: 50
I:
S:
Вещественная полуось гиперболы, заданной
уравнением
![]() ,
равна…
,
равна…
+: 3
I:
S:
Мнимая полуось гиперболы, заданной
уравнением
![]() ,
равна…
,
равна…
+: 2
V2: Прямая и плоскость в пространстве
I:
S:
Нормальный вектор плоскости
![]() имеет
координаты…
имеет
координаты…
-: (7; 0; – 1)
+: (7; – 1; – 1)
-: (– 7; 1; 1)
-: (7; 0; 0)
I:
S:
Уравнение прямой, проходящей через
точку
![]() перпендикулярно
плоскости
перпендикулярно
плоскости
![]() ,
имеет вид…
,
имеет вид…
-:
![]()
-:
![]()
-:
![]()
+:
![]()
I:
S:
Уравнение прямой, проходящей через
точку
![]() перпендикулярно
плоскости
перпендикулярно
плоскости
![]() ,
имеет вид…
,
имеет вид…
+:
![]()
-:
![]()
-:
![]()
-:
![]()
I:
S:
Точкой пересечения плоскости
![]() с
осью
с
осью
![]() является
…
является
…
-:
![]()
-:
![]()
-:
![]()
+:
![]()
I:
S:
Вектор
![]() перпендикулярен
плоскости
перпендикулярен
плоскости ![]() .
Тогда значение p равно …
.
Тогда значение p равно …
-: 10
-: - 6
+: - 4
-: 6
I:
S: Установите соответствие между уравнением плоскости и ее положением в пространстве
L1:
![]()
L2:
![]()
L3:
![]()
L4:
![]()
R5: проходит через ось y
R1:
параллельна оси
![]()
R2:
параллельна оси
![]()
R3:
параллельна оси
![]()
R4: проходит через начало координат
I:
S: Установите соответствие между уравнением плоскости и ее положением в пространстве
L1:
![]()
L2:
![]()
L3:
![]()
L4:
![]()
R3:
параллельна оси
![]()
R4: проходит через начало координат
R5:
проходит через ось
![]()
R1:
параллельна оси
![]()
R2:
параллельна оси
![]()
I:
S: Установите соответствие между уравнением плоскости и ее положением в пространстве
L1:
![]()
L2:
![]()
L3:
![]()
L4:
![]()
R1:
параллельна оси
![]()
R2:
параллельна оси
![]()
R5: проходит через ось x
R4: проходит через начало координат
R3:
параллельна оси
![]()
I:
S: Укажите соответствие между уравнением плоскости и ее положением в пространстве
L1:
![]()
L2:
![]()
L3:
![]()
R3:
параллельна оси
![]()
R2:
параллельна плоскости
![]()
R1:
параллельна плоскости
![]()
R4:
параллельна плоскости
![]()
I:
S: Установите соответствие между уравнением плоскости и точками, которые лежат в этих плоскостях
L1:
![]()
L2:
![]()
L3:
![]()
L4:
![]()
R5:
![]()
R3:
![]()
R2:
![]()
R1:
![]()
R4:
![]()
V2: Квадратичные формы
I:
S:
Матрице
 соответствует
квадратичная форма …
соответствует
квадратичная форма …
+:
![]()
-:
![]()
-:
![]()
-:
![]()
I:
S:
Матрице
 соответствует
квадратичная форма …
соответствует
квадратичная форма …
-:
![]()
-:
![]()
+:
![]()
-:
![]()
I:
S:
Матрице
 соответствует
квадратичная форма …
соответствует
квадратичная форма …
-:
![]()
+:
![]()
-:
![]()
-:
![]()
I:
S:
Матрице
 соответствует
квадратичная форма …
соответствует
квадратичная форма …
-:
![]()
-:
![]()
-:
![]()
+:
![]()
I:
S:
Матрице
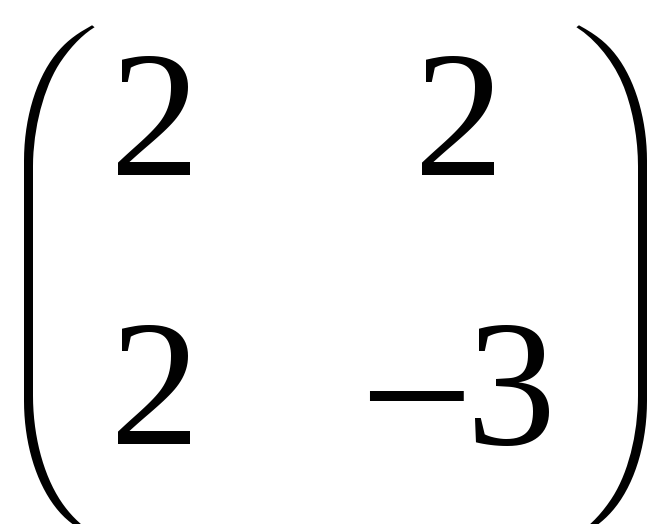 соответствует
квадратичная форма …
соответствует
квадратичная форма …
+:
![]()
-:
![]()
-:
![]()
-:
![]()
I:
S:
Матрице
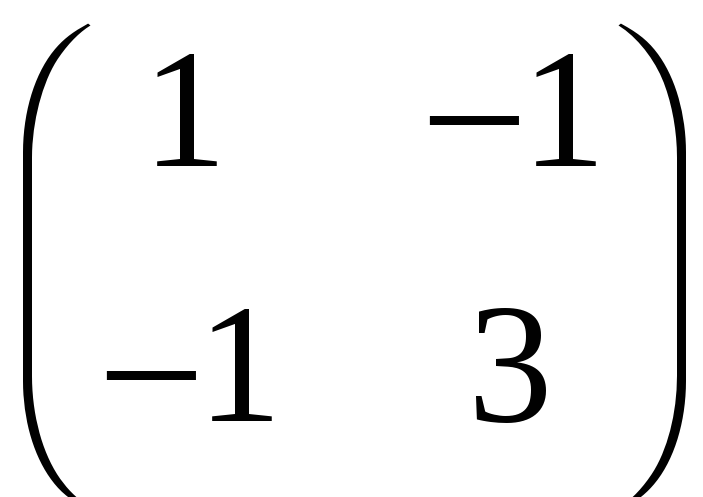 соответствует
квадратичная форма …
соответствует
квадратичная форма …
-:
![]()
-:
![]()
+:
![]()
-:
![]()
I:
S:
Матрице
 соответствует
квадратичная форма …
соответствует
квадратичная форма …
-:
![]()
-:
![]()
-:
![]()
+:
![]()
