
080100Экономика(МатАнализ и ЛинАлгебра) / Лекции_Математический анализ
.pdf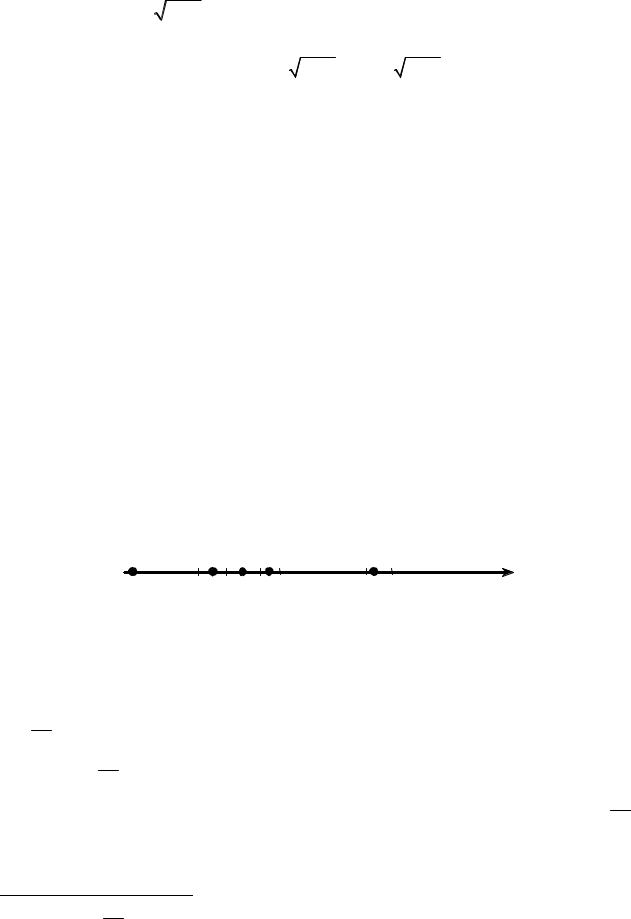
|
x −1 |
|
t 2tdt |
|
|
|
|
1 |
|
|
||
∫ |
|
dx = ∫ |
|
2 |
|
= 2∫ 1 |
− |
|
|
|
|
dt = |
x |
t |
+1 |
t |
2 |
|
|
||||||
|
|
|
|
|
|
+1 |
||||||
= 2(t − arctg t) + C = 2( |
x −1 − arctg |
x −1)+ C . |
||||||||||
3.4.Определенный интеграл
3.4.1.Задачи, приводящие к понятию определенного интеграла
К понятию определенного интеграла приводят различные задачи физики, механики, геометрии, техники. Рассмотрим три такие задачи.
3.4.1.1. Задача о длине пути
Постановка задачи. Тело движется прямолинейно с переменной скоростью v =v(t) . Требуется найти путь L, пройденный телом с момента времени
t = a |
до момента времени t = b . |
|
|
|
|
Решение задачи. В частном случае, когда скорость v постоянна, из физи- |
|||
ки известна формула L =v(b − a) . |
|
|
||
|
Рассмотрим общий случай, когда скорость является функцией времени t, |
|||
то есть v =v(t) . |
|
|
|
|
|
ξ1 ξ2 |
ξ3 |
ξn |
|
|
O t0 = a t1 |
t2 t3 |
tn−1 tn = b |
t |
|
|
РИС. 3.4.1 |
|
|
|
Построим числовую ось (рис. 3.4.1), соответствующую изменению време- |
|||
ни t. |
Разобьем отрезок [a,b] |
произвольным образом |
на n частей: [tk−1,tk ], |
|
k =1,n ,7 (здесь t0 = a , tn = b ). Обозначим длины полученных промежутков че-
рез tk , k =1,n .
В каждом промежутке выберем произвольную точку ξk [tk −1,tk ], k =1,n .
7 Запись k =1,n означает, что k принимает все целые значения от 1 до n, включительно.
71

Найдем значение пути L на каждом промежутке tk приближенно, счи-
тая, что скорость на нем постоянна и равна значению скорости в точке ξk :
Lk ≈ v(ξk ) tk , k =1,n .
Тогда для всего пути L получим приближенную формулу
L = L1 + L2 +…+ Ln ≈ v(ξ1) t1 + v(ξ2 ) t2 +…+ v(ξn ) tn .
Для записи полученной формулы воспользуемся символом суммы Σ (греческая буква «сигма»), тогда
n
L ≈ ∑v(ξk ) tk .
k=1
Точное значение пути L найдем, если перейдем в полученном равенстве к пределу, увеличивая количество промежутков разбиения и устремляя длину максимального промежутка к нулю
|
n |
|
L = lim |
∑v(ξk ) tk . |
(11) |
n→∞ |
|
|
max tk →0 k=1 |
|
|
3.4.1.2. Задача о массе стержня
Постановка задачи. Дан тонкий материальный стержень, расположенный на отрезке [a,b] оси x (рис. 3.4.2). Найти массу m этого стержня, если из-
вестна его линейная плотность ρ=ρ(x) .
ξ1 ξ2 ξ3 |
ξn |
|
O x0 = a x1 x2 x3 |
xn−1 xn = b |
x |
РИС. 3.4.2
Решение задачи. В частном случае, когда ρ = const , имеем m =ρ(b − a).
Рассмотрим общий случай, когда ρ=ρ(x) .
Разобьем отрезок [a,b] оси Ox произвольным образом на n частей:
[xk −1, xk ], k =1,n , длины которых обозначим через xk .
Выберем произвольно точки ξk [xk−1, xk ], k =1,n .
72
Найдем массу mk каждой k-ой части приближенно, считая плотность этой части постоянной и равной ρ(ξk ) :
mk ≈ ρ(ξk ) xk .
Тогда для массы m всего стержня получим приближенную формулу
n |
|
|
|
m ≈ ∑ρ(ξk ) xk . |
|
||
k=1 |
|
|
|
Точное значение массы m получим по формуле |
|
||
|
|
n |
|
m = lim |
|
∑ρ(ξk ) xk . |
(12) |
n→∞ |
|
|
|
max x |
→0 k=1 |
|
|
k |
|
|
|
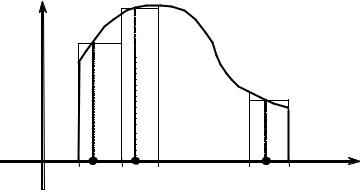
3.4.1.3. Задача о вычислении площади криволинейной трапеции
Прежде, чем перейти к постановке и решению задачи, дадим определение. Криволинейной трапецией называется плоская фигура, ограниченная осью 0x, вертикальными прямыми x = a , x = b и графиком функции y = f (x)
(рис. 3.4.3).
y |
|
y = f (x) |
|
|
|
|
|
|
|
ξ1 |
ξ2 |
ξn |
|
|
O x0 = a x1 |
x2 |
xn−1 |
xn = b |
x |
РИС. 3.4.3
Постановка задачи. Найти площадь криволинейной трапеции, ограниченной осью Ox, вертикальными прямыми x = a , x = b и графиком функции y = f (x) , f (x) ≥0 , x [a,b].
Решение задачи. В частном случае, когда f (x) =C =const , криволиней-
ная трапеция является прямоугольником с основанием b − a и высотой C, а ее площадь находится по формуле S =C(b − a).
73

Больший интерес представляет общий случай, когда функция отлична от постоянной, то есть y = f (x) .
Основание трапеции – отрезок [a,b] оси Ox разобьем произвольным обра-
зом на n частей: [xk −1, xk ], k =1,n , длины которых обозначим через xk . Прове-
дем через точки деления прямые, параллельные оси Oy. Тогда криволинейная
трапеция разобьется на n полосок. |
|
|
|
Выберем произвольно точки ξk [xk−1, xk ], |
k = |
|
и найдем значения |
1,n |
|||
функции y = f (x) в этих точках: yk = f (ξk ) . |
|
|
|
Найдем площадь Sk каждой k-ой полоски приближенно, считая полоску |
|||
прямоугольником с высотой f (ξk ) и основанием |
xk . Тогда |
||
Sk ≈ f (ξk ) xk ,
а площадь всей криволинейной трапеции найдется по приближенной формуле
n
S ≈ ∑ f (ξk ) xk .
k=1
Перейдя к пределу при стремлении максимальной длины участка разбиения отрезка [a,b] к нулю, получим точную формулу для площади криволиней-
ной трапеции
|
|
n |
|
S = lim |
|
∑ f (ξk ) xk . |
(13) |
n→∞ |
|
|
|
max x |
→0 k=1 |
|
|
k |
|
|
|
3.4.2. Определение определенного интеграла
Нами были рассмотрены три различные задачи. Однако если отвлечься от их конкретного содержания, то решение каждой из них было связано с одинаковыми математическими выкладками. Все задачи свелись к вычислению предела суммы определенного вида (см. формулы (11)-(13)), что вызывает необходимость ввести новое понятие, связанное с таким пределом.
Рассмотрим функцию y = f (x) на отрезке x [a,b] и выполним следую-
щие построения.
74

1. |
Разобьем отрезок [a,b] произвольным образом на n частей: [xk −1, xk ], |
||||
k = |
|
, |
(здесь x0 = a , xn =b) и положим xk = xk − xk−1 , k = |
|
. |
1,n |
1,n |
||||
2.В каждом отрезке [xk −1, xk ] выберем произвольную точку ξk и найдем значения функции f (ξk ) .
3.Составим сумму
n
∑ f (ξk ) xk .
k=1
Эта сумма называется интегральной суммой для функции f (x) на от-
резке [a,b] . Она зависит от способа разбиения отрезка [a,b] на части и от вы-
бора точек ξk .
4. Если существует конечный предел последовательности интегральных сумм при max xk → 0 , не зависящий ни от способа разбиения отрезка [a,b] на части, ни от выбора точек ξk , то этот предел называется определенным инте-
гралом от функции f (x) на отрезке [a,b] и обозначается
b
∫ f (x)dx .
a
Таким образом, по определению
b |
|
n |
∫ f (x)dx = |
nlim→∞ |
∑ f (ξk ) xk . |
a |
max xk →0 k=1 |
|
Число a называется нижним пределом интегрирования, b – верхним пределом интегрирования, отрезок [a,b] – отрезком интегрирования.
Возвращаясь к задачам, рассмотренным в пунктах 3.4.1.1-3.4.1.3, можно записать полученные там формулы (11)-(13) для пути L, массы m и площади S в следующем виде:
b |
b |
b |
L = ∫v(t)dt , m = ∫ρ(x)dx , S = ∫ f (x)dx . |
||
a |
a |
a |
Последняя формула дает геометрический смысл определенного интегра-
ла.
75

b
Если f (x) ≥0 при x [a,b], то ∫ f (x)dx – это площадь криволинейной
a
трапеции с основанием [a,b] , ограниченной графиком функции y = f (x) .
3.4.3.Основные свойства определенного интеграла
3.4.3.1.Свойства линейности определенного интеграла
Теорема 10. Интеграл от суммы равен сумме интегралов
b |
b |
b |
∫[f1 (x) + f2 (x)]dx = ∫ f1(x)dx + ∫ f2 (x)dx . |
||
a |
a |
a |
Доказательство. Воспользуемся определением интеграла и свойством: предел суммы равен сумме пределов. Тогда
b |
|
(x)]dx = |
|
|
n |
|
|
|
∫[f1(x) + f2 |
lim |
→0 |
∑[f1(ξk ) + f2 (ξk )] xk = |
|||||
a |
|
|
max xk |
k=1 |
|
|
||
|
|
n |
|
|
|
n |
||
|
|
|
|
|
|
|
||
= maxlimx |
→0 |
∑ f1(ξk ) |
xk |
+ maxlimx |
→0 |
∑ f2 (ξk ) xk = |
||
k |
|
|
k=1 |
|
|
k |
|
k=1 |
bb
=∫ f1 (x)dx + ∫ f2 (x)dx .
aa
Теорема 11. Постоянный множитель можно выносить за знак интеграла
b |
b |
∫Cf (x)dx = C∫ f (x)dx , C = const .
a |
a |
Доказательство.
b
∫Cf (x)dx =
a
|
|
n |
maxlimx |
→0 |
∑Cf (ξk ) xk = |
k |
|
k=1 |
|
|
n |
= C maxlimx |
→0 |
∑ f (ξk ) |
k |
|
k=1 |
b
xk = C∫ f (x)dx .
a
3.4.3.2. Перестановка пределов интегрирования в определенном интеграле
Теорема 12. При перестановке пределов интегрирования определенный интеграл меняет знак
b |
a |
∫ f (x)dx = −∫ f (x)dx .
a |
b |
76

a
Доказательство. При введении определенного интеграла ∫ f (x)dx пред-
b
полагалось, что a < b . Если же a > b , то изменится направление интервала интегрирования. Следовательно, изменится знак разностей xk = xk − xk−1 , инте-
гральной суммы и самого интеграла. Таким образом
b |
a |
∫ f (x)dx = −∫ f (x)dx . |
|
a |
b |
|
a |
Следствие. |
∫ f (x)dx = 0 . |
|
a |
3.4.3.3. Свойство аддитивности определенного интеграла
Теорема 13. Для любых трех чисел a, b и c справедливо равенство
b c b
∫ f (x)dx = ∫ f (x)dx + ∫ f (x)dx .
a a c
Доказательство.
1. Рассмотрим сначала случай, когда a < c < b .
Интегральную сумму на отрезке [a,b] обозначим ∑ f (ξk ) xk . Так как
[a,b]
предел последовательности интегральных сумм не зависит от способа разбиения отрезка [a,b] на части, то выберем такое разбиение, в котором точка c яв-
ляется точкой деления. Тогда интегральная сумма |
∑ f (ξk ) |
xk разобьется на |
|||
|
|
|
|
[a,b] |
|
две суммы. |
Сумма |
∑ f (ξk ) xk |
соответствует |
отрезку |
[a,c], а сумма |
|
|
[a,c] |
|
|
|
∑ f (ξk ) xk |
– отрезку [c,b]: |
|
|
|
|
[c,b] |
|
|
|
|
|
|
∑ f (ξk ) xk = ∑ f (ξk ) xk + ∑ f (ξk ) xk . |
|
|||
|
[a,b] |
[a,c] |
[c,b] |
|
|
Перейдя к пределу при max xk → 0 , получим |
|
|
|||
|
b |
c |
b |
|
|
|
∫ f (x)dx = ∫ f (x)dx + ∫ f (x)dx . |
|
|||
|
a |
a |
c |
|
|
|
|
|
77 |
|
|

2. Рассмотрим теперь случай |
a < b < c . В силу доказанного для первого |
|
случая имеем |
|
|
c |
b |
c |
∫ f (x)dx = ∫ f (x)dx + ∫ f (x)dx |
||
a |
a |
b |
или (с учетом теоремы 3)
b |
c |
c |
c |
b |
∫ f (x)dx = ∫ f (x)dx − ∫ f (x)dx = ∫ f (x)dx + ∫ f (x)dx . |
||||
a |
a |
b |
a |
c |
3.4.3.4. Интегрирование неравенств |
|
|
||
Теорема 14. Если |
f (x) ≥0 на отрезке [a,b] , причем a < b , то |
|||
|
|
b |
|
|
∫ f (x)dx ≥ 0 .
a
n
Доказательство. В интегральной сумме ∑ f (ξk ) xk все слагаемые неот-
|
|
|
|
k=1 |
|
рицательны, так как f (x) ≥0 и |
xk |
≥ 0 по условию теоремы. Следовательно, |
|||
b |
|
|
n |
|
|
∫ f (x)dx = lim |
∑ f (ξk ) |
xk ≥ 0 . |
|
||
a |
max |
xk →0 k=1 |
|
|
|
Следствие. Если |
f (x) ≤0 на отрезке [a,b] , причем a < b , то |
|
|||
|
b |
|
|
|
|
|
∫ f (x)dx ≤ 0 . |
|
|
||
Теорема 15. Если |
a |
|
f (x) и |
g(x) удовлетворяют |
|
функции |
условию |
||||
f (x) ≤ g(x) на отрезке [a,b] , причем a < b , то |
|
|
|||
|
b |
|
b |
|
|
|
∫ f (x)dx ≤ ∫g(x)dx . |
|
|||
|
a |
|
a |
|
|
Доказательство. По условию теоремы функция g(x) − f (x) ≥0 |
на отрез- |
||||
ке [a,b] . Тогда применима теорема 5:
b
∫[g(x) − f (x)]dx ≥ 0 .
a
Если использовать свойства линейности интеграла (п. 3.4.3.1), то получим
b b
∫g(x)dx − ∫ f (x)dx ≥ 0.
a a
78
Следовательно,
|
b |
b |
|
|
|
∫ f (x)dx ≤ ∫g(x)dx . |
|
|
|
|
a |
a |
|
|
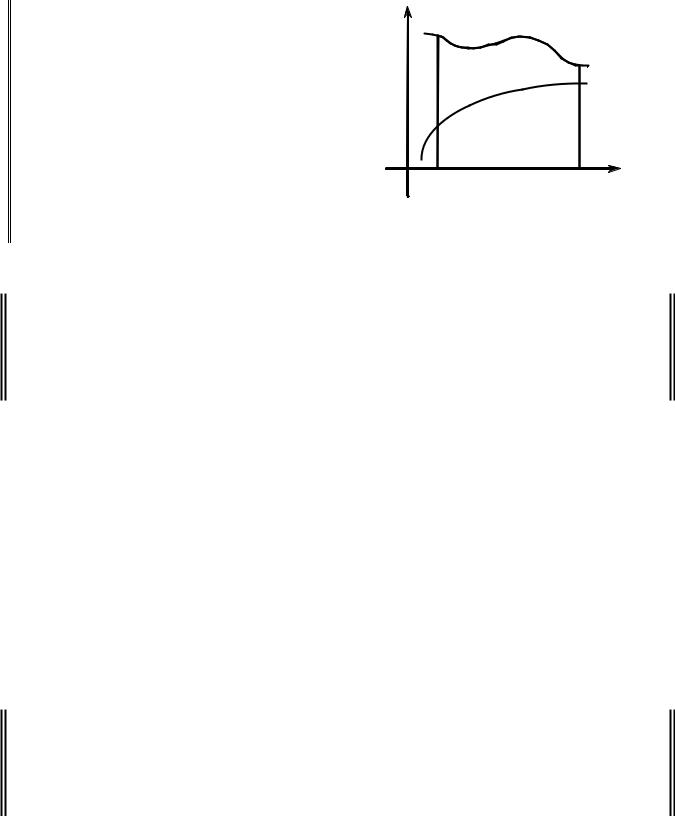
Геометрический смысл теоремы (рис. y |
y = g(x) |
|
||
3.4.4). Если |
f (x) ≥0 , g(x) ≥ 0 и |
f (x) ≤ g(x) |
|
|
при x [a,b], то площади криволинейных |
|
|
||
трапеций, |
ограниченных графиками этих |
|
y = f (x) |
|
функций, удовлетворяют неравенству |
|
|||
|
|
|||
|
S f (x) ≤ Sg (x) . |
|
|
|
|
|
O a |
b |
x |
|
|
|
РИС. 3.4.4 |
|
3.4.3.5. Интеграл от единицы
Теорема 16. Определенный интеграл от единицы по отрезку [a,b] равен длине отрезка b − a
b
∫1 dx = b − a .
a
Доказательство. Из вида интеграла следует, что f (x) =1. Тогда при лю-
бом выборе точек ξk |
имеем f (ξk ) =1, а интегральная сумма равна |
|||
n |
|
|
n |
n |
∑ f (ξk ) xk = ∑1 |
xk = ∑ xk = b − a . |
|||
k=1 |
|
|
k=1 |
k=1 |
Итак, интегральная сумма при любом разбиении отрезка на части и при |
||||
любом выборе точек ξk равна b − a . Следовательно, |
||||
b |
|
|
n |
|
∫1 dx = |
lim |
→0 |
∑ xk = |
lim (b − a) = b − a . |
a |
max xk |
k=1 |
max xk →0 |
|
|
|
|
||
3.4.3.6. Теорема об оценке определенного интеграла
Теорема 17. Если m – наименьшее, а M – наибольшее значения функции f (x) на отрезке [a,b] , a < b , то имеет место оценка
b
m(b − a) ≤ ∫ f (x)dx ≤ M (b − a) .
a
Доказательство. Так как по условию теоремы m ≤ f (x) ≤ M , то по свой-
ству интегрирования неравенств (Теорема 15) получим
79
|
b |
b |
b |
|
|
|
|
|
∫mdx ≤ ∫ f (x)dx ≤ ∫Mdx . |
|
|
|
|||
|
a |
a |
a |
|
|
|
|
Применив теперь свойство линейности (Теорема 11), найдем |
|
|
|||||
|
b |
b |
b |
|
|
|
|
|
m∫dx ≤ ∫ f (x)dx ≤ M ∫dx . |
|
|
|
|||
b |
a |
a |
a |
|
|
|
|
|
|
|
|
|
|
|
|
Так как ∫dx = (b − a) (Теорема 16), то окончательно получим |
|
|
|||||
a |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
m(b − a) ≤ ∫ f (x)dx ≤ M (b − a) . |
|
|
|
|||
|
|
a |
|
|
|
|
|
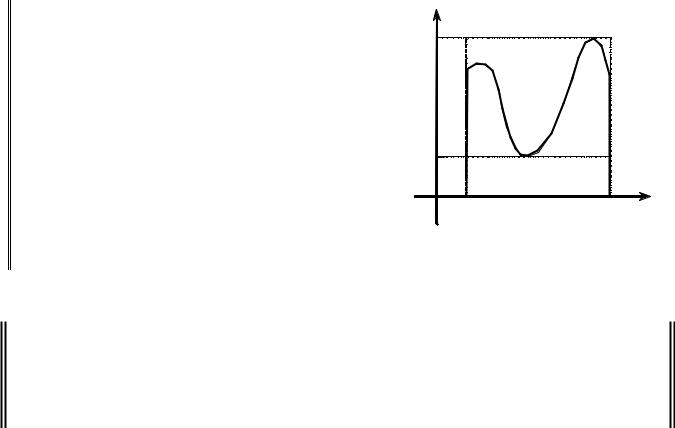
Геометрический |
смысл |
теоремы |
(рис. |
y |
A2 |
B2 |
|
3.4.5). Если f (x) ≥0 |
при x [a,b], то площадь |
M |
|
||||
|
|
|
|||||
криволинейной трапеции S f (x) |
больше площа- |
|
y = f (x) |
|
|
||
ди прямоугольника aA1B1b и меньше площади |
|
|
|
||||
|
|
|
|
||||
прямоугольника aA2 B2b : |
|
|
|
|
|
|
|
SaA1B1b ≤ S f ( x) ≤ SaA2B2b . |
|
m |
A |
B1 |
|
||
|
|
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
O a |
b |
x |
|
|
|
|
|
|
РИС. 3.4.5 |
|
|
3.4.3.7. Теорема о среднем |
|
|
|
|
|
||
Теорема 18. Если функция f (x) непрерывна на отрезке [a,b] , |
a < b , то |
||||||
на этом отрезке существует такая точка c, что выполняется равенство |
|
|
|||||
|
b |
|
|
|
|
|
|
|
∫ f (x)dx = f (c)(b − a) . |
|
|
|
|||
|
a |
|
f (x) |
непрерывна на отрезке [a,b] , то |
|||
Доказательство. Так как функция |
|||||||
она принимает на этом отрезке свое наименьшее m и наибольшее M значения. Следовательно, в силу теоремы об оценке интеграла (Теорема 17), имеем
b
m(b − a) ≤ ∫ f (x)dx ≤ M (b − a) .
a
Отсюда
80
