
080100Экономика(МатАнализ и ЛинАлгебра) / Лекции_Математический анализ
.pdf
∞ dx |
= |
∞ dx |
= ln x |
|
∞ |
= lim ln x − ln a = ∞ интеграл расходится. |
||||||||||||
|
||||||||||||||||||
∫ |
x |
p |
|
∫ |
x |
|
|
a |
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
a |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. Пусть p ≠1. Тогда |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
∞ |
|
|
∞ |
|
x−p+1 |
|
∞ |
|
∞−p+1 |
|
a−p+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
∫ dxp = |
|
∫x−pdx = |
|
|
= |
− |
= |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
a |
x |
|
a |
|
−p +1 |
|
a |
|
−p +1 |
−p +1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
∞ |
|
|
если p <1 интеграл расходитстя, |
|||||||||
|
|
|
|
|
|
a−p +1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
= |
|
|
|
|
интеграл сходитстя. |
|||||||||
|
|
|
|
|
− |
−p +1 |
если p >1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∞ |
dxp |
|
сходитстя при |
p >1, |
|
Итак, ∫ |
|||||
− |
|
p ≤1. |
|||
a |
x |
расходитстя при |
|||
3.6.3.Несобственные интегралы от неограниченных функций
3.6.3.1.Определение несобственных интегралов
Пусть функция y = f (x) непрерывна на интервале [a,b) оси Ox и пусть
lim f (x) = ∞. Выберем произвольное число ε > 0 и рассмотрим определенный
x→b
b−ε
интеграл ∫ f (x)dx от ограниченной на отрезке [a,b − ε] функции y = f (x) .
a
Несобственным интегралом от функции y = f (x) , неограниченной при
x →b называется
b−ε
lim ∫ f (x)dx .
ε→0 a
Если указанный предел существует, то несобственный интеграл называется сходящимся, а если не существует, то – расходящимся.
Итак, по определению
b |
|
b−ε |
∫ f (x)dx = |
ε→lim0 |
∫ f (x)dx . |
a |
|
a |
101
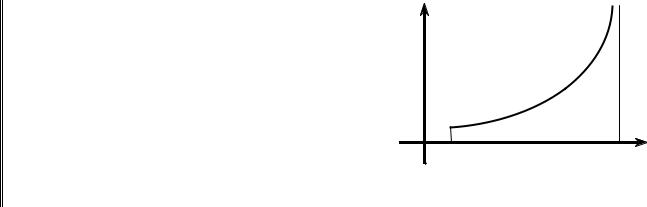
|
y |
|
Геометрический смысл |
несобственного |
|
интеграла. |
y = f (x) |
|
b |
|
|
Если f (x) ≥0 , то ∫ f (x)dx |
– это площадь |
|
a |
|
|
бесконечной криволинейной трапеции (рис. O a |
b x |
|
3.6.2). |
РИС. 3.6.2 |
|
|
|
|
Аналогично определяется несобственный интеграл от функции |
y = f (x) , |
|
непрерывной на промежутке (a,b] |
и неограниченной при x →a , то есть при |
|
lim f (x) = ∞. По определению |
|
|
x→a |
|
|
b |
|
b |
∫ f (x)dx = |
ε→lim0 ∫ f (x)dx . |
|
a |
|
a+ε |
Если функция y = f (x) |
имеет внутри промежутка [a,b] точку бесконеч- |
|
ного разрыва x =c , то |
|
|
b |
c |
b |
∫ f (x)dx = ∫ f (x)dx + ∫ f (x)dx , |
||
a |
a |
c |
b
причем несобственный интеграл ∫ f (x)dx сходится, если сходятся оба инте-
a
грала, стоящие в правой части формулы, и расходится, если расходится хотя бы один из них.
3.6.3.2. Вычисление несобственных интегралов |
|
|
|
|||||||||||
Пусть F(x) – |
первообразная для функции f (x) , неограниченной при |
|||||||||||||
x →b . Тогда, |
используя |
определение |
несобственного |
интеграла и формулу |
||||||||||
Ньютона-Лейбница, получим |
|
|
|
|
|
|
|
|
|
|||||
b |
|
|
b−ε |
|
|
|
|
b−ε = lim |
[ |
|
|
] |
|
|
∫ |
f (x)dx = lim |
∫ |
f (x)dx = lim F (x) |
|
F(b − ε) − F(a) |
= |
||||||||
|
||||||||||||||
|
ε→0 |
|
ε→0 |
|
|
a |
ε→0 |
|
|
|
||||
|
|
|
|
|
|
|
||||||||
a |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
= lim F(b − ε) − F (a) = F(b − 0) − F (a) ,
ε→0
где F (b − 0) = lim F (b − ε) .
ε→0
102

Аналогично, если F(x) – первообразная для функции f (x) , неограничен-
ной при x →a , то
b |
|
|
∫ |
f (x)dx = F (b) − F (a + 0), |
F (a + 0) = lim F (a + ε) . |
|
ε→0 |
|
a |
|
|
Пример.
1 dx
Найти ∫a 1 − x2 .
Решение.
1 |
dx |
|
|
10 |
|
∫ |
= arcsin x |
|
|||
|
|||||
|
|||||
0 |
1 − x2 |
|
|
||
|
|||||
= arcsin1 − arcsin 0 = π2 .
Интеграл сходится.
b dx
3.6.3.3. Исследование сходимости интеграла ∫a (x − b) p
В различных разделах высшей математики и в ее приложениях, наряду с несобственным интегралом, исследованным в п. 3.6.2.3, также часто использу-
b dx
ются несобственные интегралы вида ∫a (x − b) p . Поэтому проведем исследова-
ние сходимости в зависимости от величины параметра p8. 1. Пусть p =1. Тогда
b |
dx |
|
b |
dx |
|
|
|
|
|
ba = ln 0 − ln |
|
|
|
|
|
∫ |
|
= ∫ |
= ln |
|
x − b |
|
|
|
a − b |
|
= ∞ |
||||
|
|
|
|
||||||||||||
|
|
|
|
|
|||||||||||
(x − b) |
p |
x − b |
|||||||||||||
|
|
|
|
||||||||||||
a |
|
a |
|
|
|
|
|
|
|
|
|
|
интеграл расходится.
2. Пусть p ≠1. Тогда
b |
dx |
|
b |
(x −b)−p+1 |
|
b |
|
0−p+1 |
|
|
(a −b)−p+1 |
|
|
|
|
|
|
||||||||
∫ |
|
= ∫(x −b)−p dx = |
|
|
= |
− |
= |
|||||
(x −b) |
p |
−p +1 |
|
|
−p +1 |
−p +1 |
||||||
a |
|
a |
|
a |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
8 Отметим, что рассматриваемый интеграл является несобственным лишь при p > 0 , однако приводимое ниже исследование сходимости справедливо при любых значениях p.
103
|
|
|
∞ |
|
если p >1 |
интеграл расходится, |
||
|
|
(a − b)−p +1 |
|
|
||||
= |
|
если p <1 |
интеграл сходится. |
|||||
− |
|
|
|
|
||||
−p +1 |
||||||||
|
|
|
|
|||||
b |
|
dx |
|
|
сходится при |
p <1, |
||
Итак, ∫ |
|
|
|
|||||
|
|
|
− |
|
|
|||
|
|
p |
|
p ≥1. |
||||
a |
(x − b) |
|
|
расходится при |
||||
104

РАЗДЕЛ III. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Тема 4. Дифференциальные уравнения
4.1.Дифференциальные уравнения, основные понятия
4.1.1.Основные определения
Прежде, чем ввести понятие дифференциального уравнения, напомним, что в элементарной математике уравнением (алгебраическим, тригонометрическим, показательным и т. д.) называлось равенство, содержащее неизвест-
ную величину x. Решение такого уравнения – это значение x, обращающее уравнение в тождество. Уравнение может быть неразрешимо либо иметь одно, несколько или бесконечное множество решений.
Отличительной особенностью ДУ является то, что в них в качестве неизвестной выступает не величина, а функция одной или нескольких переменных.
Дифференциальным уравнением называется уравнение, связывающее неизвестную функцию, ее производные различных порядков и независимые переменные.9
|
Примеры. |
|
|
|||
1) |
y′′ − ky = 0 , y(x) – ?; |
|||||
2) |
′′ |
|
′′ |
|
z(x, y) – ?; |
|
zxx |
+ zyy = 0 , |
|||||
3) |
′′′ |
|
3 |
, |
ϕ(x) – ? |
|
ϕ = x |
|
|||||
Дифференциальное уравнение, содержащее неизвестную функцию одной переменной, называется обыкновенным ДУ (примеры 1, 3). Если же неизвестная функция зависит от нескольких переменных, то ДУ называется ДУ в
частных производных.
В настоящем курсе мы остановимся лишь на изучении обыкновенных
ДУ10.
9 Здесь и далее двойной толстой вертикальной чертой слева абзаца будут отмечаться основные определения.
105

Порядком ДУ называется наивысший порядок производных, входящих в уравнение.
Примеры.
1)F (x, y, y′) = 0 – ДУ первого порядка;
2)F (x, y, y′, y′′) = 0 – ДУ второго порядка;
′ |
(n) |
) = 0 – ДУ n-го порядка. |
3) F(x, y, y ,…, y |
|
Решением ДУ называется функция y = y(x) , обращающая уравнение в тождество, то есть в равенство, справедливое при любых значениях независимой переменной x.
Примеры. |
|
Рассмотрим ДУ |
|
y′ = y / x . |
(22) |
Функция y = Cx , где C – произвольная постоянная, является решением |
|
этого ДУ. В этом нетрудно убедиться, если найти производную |
y′ = C и под- |
ставить ее вместе с самой функцией в уравнение (22): |
|
C = Cx C = C . |
|
x |
|
Пришли к тождеству, справедливому при любых значениях x. |
|
Рассмотрим теперь ДУ |
|
y′′ + y = 0 . |
(23) |
Решением этого ДУ будет функция |
|
y = sin x . |
(24) |
Чтобы проверить это, найдем y′ = cos x , y′′ = −sin x . Подставив выражения y(x)
и |
′′ |
|
y (x) в уравнение (23), получим |
|
|
|
−sin x + sin x ≡ 0 . |
|
Опять пришли к тождеству. |
|
|
|
Аналогично можно показать, что функция |
|
|
y = cos x |
(25) |
10 Далее под сокращением «ДУ» будем понимать «обыкновенные дифференциальные уравнения».
106

также будет решением уравнения (23);
y′ = −sin x , y′′ = −cos x −cos x + cos x ≡ 0.
Если теперь взять линейную комбинацию этих двух решений
y = C1 sin x + C2 cos x , |
(26) |
где C1 , C2 – произвольные постоянные, то опять получим решение ДУ (23) (проверку этого утверждения выполнить самостоятельно).
4.1.2. Общее и частное решения ДУ
Приведенные выше примеры показывают, что ДУ может иметь бесконечное множество решений, отличающихся друг от друга значениями произволь-
ных постоянных. |
|
|
||
Решение ДУ, |
содержащее произвольные постоянные |
( y = y(x,C) , |
||
y = y(x,C ,C |
2 |
) , …), называется общим решением ДУ11. |
|
|
1 |
|
|
|
|
Если |
|
общее |
решение задано в неявном виде |
F (x, y,C) = 0 , |
F (x, y,C1,C2 ) = 0 , …, то его называют общим интегралом ДУ.
Решение ДУ, получающееся из общего решения при конкретных значениях постоянных, называется частным решением ДУ.
Если частное решение задано в неявном виде F (x, y) = 0 , то оно называ-
ется частным интегралом ДУ.
В приведенном выше примере функция (26) является общим решением уравнения (23), функция (24) – частным решением при C1 =1, C2 = 0 , а (25) –
частным решением при C1 = 0 , C2 =1.
4.2.Дифференциальные уравнения первого порядка
4.2.1.Определение и различные формы записи ДУ первого порядка
ДУ первого порядка – это ДУ, содержащее в своей записи неизвестную функцию y(x) , ее первую производную y′(x) и независимую переменную x.
11 Более точное определение общего решения мы дадим в дальнейшем на примерах ДУ первого (см. с. 7) и второго порядков (см. с. 14).
107

Для ДУ первого порядка различают три основные формы записи: общая форма
|
′ |
(27) |
|
F (x, y, y ) = 0 ; |
|
нормальная форма (разрешенная относительно производной) |
|
|
|
y′ = f (x, y) ; |
(28) |
дифференциальная форма |
|
|
M (x, y)dx + N (x, y)dy = 0 . |
(29) |
|
Примеры. |
|
|
1) xy′ − y2 = 0, |
– ДУ в общей форме; |
|
2) sin( y′2 + 2y) =5x y′ |
|
|
|
|
|
3) y′ = 2x + y −1 |
– ДУ в нормальной форме; |
|
4) (x2 +1)dy + xydx = 0 |
– ДУ в дифференциальной форме. |
|
Из приведенных примеров видно, что в некоторых случаях ДУ в форме (27) можно преобразовать в форму (28) (пример 1). Однако это возможно не всегда (пример 2). Переход от формы (28) к форме (29) и наоборот всегда можно произвести, если воспользоваться формулой
y′ = |
dy |
|
dx . |
(30) |
Примеры.
Переведем ДУ y′ = y x+1 из нормальной формы записи в дифференциаль-
ную, воспользовавшись формулой (30):
|
|
dy |
= |
y +1 |
xdy = ( y +1)dx xdy − ( y +1)dx = 0 . |
|
|
||||||
|
|
dx |
|
|
|
||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
||
Переведем теперь ДУ ( y2 +1)dx − xydy = 0 из дифференциальной формы в |
|||||||||||||
нормальную: |
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
2 |
dy |
( y2 +1) |
dy |
′ |
|
( y2 +1) |
|
( y |
|
+1)dx = xydy ( y |
|
+1) = xy dx |
xy |
= dx y |
|
= |
xy |
. |
|||
108
4.2.2.Решения ДУ первого порядка
4.2.2.1.Общее решение, интегральные кривые
Совокупность решений ДУ первого порядка описывается формулой, содержащей одну произвольную постоянную. Выражение y = y(x,C) называется
общим решением ДУ первого порядка, если при любом допустимом значении C функция y = y(x,C) является решением ДУ.
Если построить график одного из решений ДУ, получающегося из общего решения при конкретном значении постоянной C, то получим кривую, называемую интегральной кривой. Общее решение ДУ будет изображаться множе-
ством интегральных кривых.
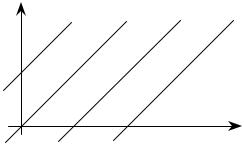
y |
y=x+1 |
y=x |
y=x–2 |
1 |
|
|
|
0 |
1 |
2 |
x |
|
РИС. 4.2.1 |
|
|
Пример. Рассмотрим ДУ y′ =1. Нетрудно видеть, что его общим решени-
ем является функция y = x + C , а интегральными кривыми – прямые линии, па-
раллельные биссектрисе первого и третьего координатных углов (рис. 4.2.1).
4.2.2.2. Частное решение, задача Коши
При решении технических задач, как правило, нужно найти одно определенное решение или построить одну вполне конкретную интегральную кривую. Этого можно добиться, если зафиксировать величину постоянной C.
Решения, получающиеся из общего решения ДУ при подстановке конкретных значений произвольной постоянной C, называются частными реше-
ниями.
109

Как видим, для получения частного решения необходимо выбрать величину постоянной. Для этого нужна дополнительная информация. Например,
можно указать, что при x = x0 |
функция принимает заданное значение y = y0 . |
||
Условие |
|
|
|
y(x ) = y |
0 |
12 |
(31) |
0 |
|
|
|
называется начальным условием. |
|
|
|
Геометрически начальное условие означает, что задана точка M 0 с координатами (x0 , y0 ) , через которую проходит интегральная кривая.13
Задачу нахождения частного решения ДУ первого порядка по заданному начальному условию называют задачей Коши и записывают в виде
y′ = |
f (x, y), |
|
|||
|
|
|
|
|
|
y |
|
0 |
= y . |
(32) |
|
|
|||||
|
|
|
|
||
|
|
x=x |
|
0 |
|
Аналогично можно записать задачи Коши для ДУ в других формах:
|
′ |
= 0, |
M (x, y)dx + N (x, y)dy = 0, |
F (x, y, y ) |
|||
|
; |
или |
|
y(x0 ) = y0 |
y(x0 ) = y0 . |
||
Теорема Коши |
(существования |
и единственности решения ДУ). Если в окрестности точки M |
|
(x0 , y0 ) функции |
f (x, y) и fy′(x, y) непрерывны, то задача Коши (32) имеет единственное решение.14 |
||
Теперь мы готовы дать полное определение общего решения.
Общим решением ДУ первого порядка называется функция y = y(x,C) ,
удовлетворяющая условиям:
1)она является решением ДУ при любом значении C;
2)при любом начальном условии (31) существует единственное значение постоянной C = C0 такое, что функция y = y(x,C0 ) удовлетворяет условию (31) (предполагается, что величины x0 и y0 принадле-
жат области, где выполняются условия теоремы Коши).
4.3. Типы ДУ первого порядка и методы их решения
Перейдем теперь к конкретным типам ДУ первого порядка и изучим методы их решения.
12Начальное условие иногда записывается в виде y x=x0 = y0 .
13Двойной тонкой вертикальной чертой слева абзаца будем отмечать геометрический или физический смысл различных понятий.
14Двойными толстыми вертикальными чертами слева и справа абзаца будем отмечать формулировки теорем.
110
