
080100Экономика(МатАнализ и ЛинАлгебра) / Математика_Словарь терминов
.pdfАВТОНОМНАЯ НЕКОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ЦЕНТРОСОЮЗА РОССИЙСКОЙ ФЕДЕРАЦИИ
«РОССИЙСКИЙ УНИВЕРСИТЕТ КООПЕРАЦИИ»
КАЗАНСКИЙ КООПЕРАТИВНЫЙ ИНСТИТУТ (ФИЛИАЛ)
Поташев А.В., Поташева Е.В.
МАТЕМАТИКА
СЛОВАРЬ ТЕРМИНОВ
для студентов, обучающихся
по специальности 036401.65 Таможенное дело
и направлениям подготовки
080100.62 Экономика, 080200.62 Менеджмент, 100100.62 Сервис,
100400.62 Туризм, 100800.62 Товароведение, 222000.62 Инноватика,
260800.62 Технология продукции и организация общественного питания
Казань 2012
Поташев А.В., Поташева Е.В. Математика. Словарь терминов. – Казань: Казанский кооперативный институт, 2012. – 20 с.
Словарь терминов по дисциплине «Математика» (цикла общих математических и естественно-научных дисциплин федерального компонента учебного плана) для специальности 036401.65 Таможенное дело и направлений подготовки 080100.62 Экономика, 080200.62 Менеджмент, 100100.62 Сервис, 100400.62 Туризм, 100800.62 Товароведение, 222000.62 Инноватика, 260800.62 Технология продукции и организация общественного питания составлен д.ф.-м.н., профессором Поташевым А.В., профессором кафедры «Ин- женерно-технические дисциплины и сервис» Казанского кооперативного института и к.т.н. Поташевой Е.В., доцентом кафедры «Инженерно-технические дисциплины и сервис» Казанского кооперативного института в соответствии с учебными планами дисциплины «Математика», утвержденными ученым советом Российского университета кооперации 22 марта 2011 г., протокол №4 и 26 апреля 2012 г., протокол №4, и рабочей программой от ______________, протокол № ___.
Словарь терминов:
обсужден и рекомендован к изданию решением кафедры «Инженернотехнические дисциплины и сервис» Казанского кооперативного института от «____» _______ 2012г., протокол №2.
Зав. кафедрой |
А.М. Мухаметшин |
одобрен Методическим советом Казанского кооперативного института от «_______» _________ 2012г., протокол № ______
Председатель |
А.М. Хуснутдинова |
© Казанский кооперативный институт (филиал) Российского университета кооперации, 2012
© Поташев А.В., Поташева Е.В., 2012

№ |
Термин |
|
|
|
|
Значение |
|
|
|
|
|
|
|
|
|
|
||||
п/п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
Абсолютно сходя- |
Сходящийся знакопеременный ряд, для кото- |
||||||||||||||||||
|
щийся ряд |
рого сходится также ряд, составленный из мо- |
||||||||||||||||||
|
|
дулей его членов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. |
Абсцисса |
Координата точки на оси Ox в прямоугольной |
||||||||||||||||||
|
|
системе координат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. |
Алгебраическое до- |
Алгебраическим дополнением Aij |
элемента aij |
|||||||||||||||||
|
полнение |
называется |
произведение |
|
|
минора |
Mij |
на |
||||||||||||
|
|
|
|
|||||||||||||||||
|
|
( 1)i |
j , то есть A |
( |
1)i j M |
ij |
. |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
ij |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4. |
Аналитическая гео- |
Раздел геометрии, в котором геометрические |
||||||||||||||||||
|
метрия |
фигуры и их свойства исследуются средствами |
||||||||||||||||||
|
|
линейной и векторной алгебры. |
|
|
|
|
|
|
||||||||||||
5. |
Аппликата |
Координата точки на оси Oz в прямоугольной |
||||||||||||||||||
|
|
системе координат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6. |
Аргумент |
См. функция. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
7. |
Аргумент комплекс- |
arg z |
arg(x |
iy) |
|
– угол (в радианах) меж- |
||||||||||||||
|
ного числа |
ду осью Ox и радиус-вектором |
OM |
|
(x, y) |
|||||||||||||||
|
|
|
||||||||||||||||||
|
|
точки, соответствующей числу z |
x |
iy . |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
8. |
Асимптота |
Прямая, обладающая свойством: расстояние от |
||||||||||||||||||
|
|
точки кривой до этой прямой стремится к ну- |
||||||||||||||||||
|
|
лю при удалении точки вдоль ветви кривой в |
||||||||||||||||||
|
|
бесконечность. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
9. |
Базис |
Множество векторов в векторном простран- |
||||||||||||||||||
|
|
стве таких, что любой вектор этого простран- |
||||||||||||||||||
|
|
ства может быть единственным образом пред- |
||||||||||||||||||
|
|
ставлен в виде линейной комбинации векторов |
||||||||||||||||||
|
|
из этого множества – базисных векторов. |
|
|||||||||||||||||
10. |
Бесконечно большая |
Последовательность {yn } называется беско- |
||||||||||||||||||
|
последовательность |
нечно большой, если для любого положитель- |
||||||||||||||||||
|
|
ного числа A найдется номер N |
|
такой, |
что |
|||||||||||||||
|
|
при всех n |
N элементы |
yn |
|
этой последова- |
||||||||||||||
|
|
тельности удовлетворяют неравенству |
|
yn |
|
A. |
||||||||||||||
|
|
|
||||||||||||||||||
11. |
Бесконечно большая |
Функция f (x) называется бесконечно боль- |
||||||||||||||||||
|
функция |
шой функцией (б.б.ф.) при x |
|
a |
(x |
|
|
) , |
||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
если функция |
|
|
– бесконечно малая функ- |
|||||||||||||||
|
|
f (x) |
||||||||||||||||||
|
|
ция при x |
a (x |
|
) , то есть |
|
|
|
|
|
|
|||||||||
|
|
|
lim |
1 |
|
0 |
lim |
|
|
1 |
|
0 . |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
f (x) |
|
f (x) |
|
|
|
|
|||||||||||
|
|
|
x a |
|
x |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
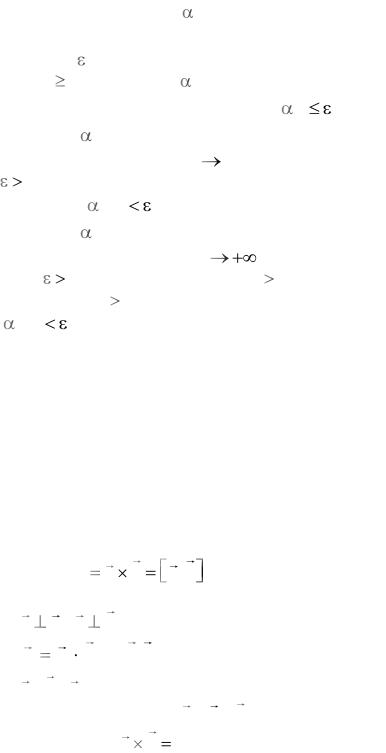
№ |
Термин |
|
|
|
|
|
|
|
|
|
|
|
|
Значение |
|
|
||||
п/п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12. |
Бесконечно малая |
Последовательность { n } называется беско- |
||||||||||||||||||
|
последовательность |
нечно малой, если для любого положительно- |
||||||||||||||||||
|
|
го числа |
|
|
|
|
найдется номер |
N такой, что при |
||||||||||||
|
|
всех n |
N элементы |
n , этой последователь- |
||||||||||||||||
|
|
ности удовлетворяют неравенству |
n |
. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
13. |
Бесконечно малая |
Функция |
(x) называется бесконечно малой |
|||||||||||||||||
|
функция в точке |
функцией (б.м.ф.) при x |
|
a , если для любого |
||||||||||||||||
|
|
|
|
0 в окрестности точки a выполняется не- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
равенство |
|
|
(x) |
. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
14. |
Бесконечно малая |
Функция |
(x) называется бесконечно малой |
|||||||||||||||||
|
функция на беско- |
функцией (б.м.ф.) при x |
|
|
, если для лю- |
|||||||||||||||
|
нечности |
бого |
|
|
0 существует число M |
0 такое, что |
||||||||||||||
|
|
при |
всех |
|
x |
M |
выполняется |
неравенство |
||||||||||||
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
(x) |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
15. |
Вектор |
Отрезок, которому приписано определенное |
||||||||||||||||||
|
|
направление, т.е. указаны начало и конец от- |
||||||||||||||||||
|
|
резка. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
16. |
Векторная алгебра |
Раздел векторного исчисления, в котором изу- |
||||||||||||||||||
|
|
чаются свойства линейных операций с векто- |
||||||||||||||||||
|
|
рами: сложение, умножение векторов на число, |
||||||||||||||||||
|
|
различные произведения векторов – скалярное, |
||||||||||||||||||
|
|
векторное, смешанное и т. д. |
|
|
||||||||||||||||
17. |
Векторное исчисле- |
Раздел математики, в котором изучаются свой- |
||||||||||||||||||
|
ние |
ства операций над векторами. |
|
|
||||||||||||||||
18. |
Векторное произве- |
Вектор |
c |
|
a |
b |
a,b |
, |
удовлетворяющий |
|||||||||||
|
дение векторов |
|
||||||||||||||||||
|
трем условиям: |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
1) c |
a , c |
|
b , |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2) |
c |
|
|
a |
|
b |
sin(a,b) , |
|
|
|
|
|
|
|||||
|
|
3) a , b , |
c – правая тройка. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
j |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
x1 |
y1 |
z1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
y2 z2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
19. |
Вогнутый график |
График функции |
f (x) называется вогнутым |
|||||||||||||||||
|
функции |
на интервале (a,b) , если он лежит над каса- |
||||||||||||||||||
|
|
тельной, проведенной к графику в любой точ- |
||||||||||||||||||
|
|
ке интервала (a,b) . |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

№ |
Термин |
|
|
|
|
|
|
Значение |
|
|
|
|
|
|
|
|||||||
п/п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20. |
Возрастающая функ- |
Функция y |
|
f (x) называется возрастающей |
||||||||||||||||||
|
ция |
на интервале (a,b) , если большему значению |
||||||||||||||||||||
|
|
аргумента |
x2 |
|
|
x1 , x1, x2 |
(a,b) соответствует |
|||||||||||||||
|
|
большее значение функции f (x2 ) |
|
f (x1) . |
||||||||||||||||||
21. |
Второй замечатель- |
|
|
|
|
1 x |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
ный предел |
lim 1 |
|
|
e или lim(1 |
|
x |
e . |
||||||||||||||
|
|
|
|
|
x) |
|||||||||||||||||
|
|
|
x |
|
||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
22. |
Выпуклый график |
График функции |
f (x) |
|
называется выпуклым |
|||||||||||||||||
|
функции |
на интервале (a,b) , если он лежит под каса- |
||||||||||||||||||||
|
|
тельной, проведенной к графику в любой точ- |
||||||||||||||||||||
|
|
ке интервала (a,b) . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
23. |
Высказывание |
Предложение, которое истинно или ложно. |
||||||||||||||||||||
24. |
Гармоника |
Функция вида y |
|
Asin( |
x |
) , |
где |
A 0 – |
||||||||||||||
|
|
амплитуда, |
|
|
|
– частота, |
– начальная фаза. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
25. |
Гармонический ряд |
|
1 |
1 |
1 |
|
1 |
|
|
1 |
|
. |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
n 1 n |
2 |
|
3 |
|
|
|
n |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
26. |
Гипербола |
Линия второго порядка, каноническое уравне- |
||||||||||||||||||||
|
|
ние которой имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
x2 |
|
|
y2 |
1. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
a2 |
b2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
27. |
График функции |
Множество точек, у которых абсциссы явля- |
||||||||||||||||||||
|
|
ются допустимыми значениями аргумента x, а |
||||||||||||||||||||
|
|
ординаты |
– |
|
соответствующими |
значениями |
||||||||||||||||
|
|
функции y |
|
f (x) . |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
28. |
Действительная |
См. комплексное число |
|
|
|
|
|
|
|
|
||||||||||||
|
часть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
29. |
Дизъюнкция |
Высказывание A |
|
B , |
которое ложно только в |
|||||||||||||||||
|
|
том случае, когда ложны оба высказывания A |
||||||||||||||||||||
|
|
и B . Дизъюнкция A |
B соответствует логиче- |
|||||||||||||||||||
|
|
ской связке «или». |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
30. |
Дифференциал функ- |
Произведение производной функции |
y f (x) |
|||||||||||||||||||
|
ции |
на приращение независимой переменной. |
||||||||||||||||||||
|
|
|
|
|
dy |
y |
|
x |
y |
dx . |
|
|
|
|
||||||||
|
|
|
||||||||||||||||||||
31. |
Дифференциальное |
Раздел математического анализа, в котором |
||||||||||||||||||||
|
исчисление |
изучаются понятия производной и дифферен- |
||||||||||||||||||||
|
|
циала и способы их применения к исследова- |
||||||||||||||||||||
|
|
нию функций. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||

№ |
Термин |
Значение |
||||
п/п |
||||||
|
|
|
|
|
||
32. |
Дифференциальное |
Уравнение, связывающее неизвестную функ- |
||||
|
уравнение |
цию, ее производные различных порядков и |
||||
|
|
независимые переменные. |
|
|||
33. |
Дифференциальное |
Дифференциальное уравнение вида |
||||
|
уравнение Бернулли |
y a(x) y |
yn f (x), |
|||
|
|
где n 0 , n 1. |
|
|
|
|
34. |
Дифференциальное |
Дифференциальное |
уравнение, содержащее |
|||
|
уравнение в частных |
неизвестную функцию нескольких перемен- |
||||
|
производных |
ных. |
|
|
|
|
35. |
Дифференциальное |
Дифференциальное уравнение вида |
||||
|
уравнение с разде- |
M (x)dx |
N( y)dy . |
|||
|
ленными перемен- |
|
|
|
|
|
|
ными |
|
|
|
|
|
36. |
Дифференциальное |
Дифференциальное уравнение вида |
||||
|
уравнение с разделя- |
M1(x)N1( y)dx |
M 2 (x)N2 ( y)dy 0 . |
|||
|
ющимися перемен- |
|
|
|
|
|
|
ными в дифференци- |
|
|
|
|
|
|
альной форме |
|
|
|
|
|
37. |
Дифференциальное |
Дифференциальное уравнение вида |
||||
|
уравнение с разделя- |
y |
f1 (x) f2 ( y) . |
|||
|
ющимися перемен- |
|
|
|
|
|
|
ными в нормальной |
|
|
|
|
|
|
форме |
|
|
|
|
|
38. |
Дифференцирование |
Операция отыскания производной функции. |
||||
39. |
Единичная матрица |
Квадратная матрица вида |
|
|||
|
|
|
1 0 0 |
0 |
||
|
|
|
0 1 0 |
0 |
||
|
|
E |
0 0 1 |
0 . |
||
|
|
|
0 0 0 |
1 |
||
|
|
|
||||
40. |
Единичный вектор |
Вектор e , модуль которого равен единице. |
||||
|
(орт) |
|
|
|
|
|
41. |
Задача Коши |
Задача нахождения решения дифференциаль- |
||||
|
|
ного уравнения, удовлетворяющего начальным |
||||
|
|
условиям. |
|
|
|
|
42. |
Знакопеременный |
Числовой ряд, содержащий как положитель- |
||||
|
ряд |
ные, так и отрицательные члены |
||||
43. |
Знакоположительный |
Числовые ряды с положительными членами. |
||||
|
ряд |
|
|
|
|
|

№ |
Термин |
|
|
Значение |
|
|||
п/п |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
44. |
Знакочередующийся |
Числовой ряд, в котором за каждым положи- |
||||||
|
ряд |
тельным членом следует отрицательный, а за |
||||||
|
|
каждым отрицательным – положительный. |
||||||
45. |
Значение истинности |
Значением |
истинности |
высказывания A |
||||
|
|
называется число |
|
( A) , |
определяемое равен- |
|||
|
|
ством: ( A) |
1, если A |
истинно, |
||||
|
|
0, |
если A |
ложно. |
|
|||
|
|
|
|
|||||
|
|
|
|
|
||||
46. |
Импликация |
Высказывание A |
|
B , которое ложно только в |
||||
|
|
том случае, |
если |
A – истинно, а B – ложно. |
||||
|
|
Импликация |
A |
B соответствует логической |
||||
|
|
связке «если …, то …». |
|
|
|
|||
47. |
Интеграл несоб- |
Интеграл от функции y |
|
f (x) на бесконечном |
||||
|
ственный 1-го рода |
|
|
|
|
|
|
t |
|
|
промежутке [a, ) : |
f (x)dx lim |
f (x)dx . |
||||
|
|
|
|
|
a |
|
t |
a |
|
|
|
|
|
|
|
||
48. |
Интеграл несоб- |
Интеграл от функции |
y |
f (x) , |
неограничен- |
|||
|
ственный 2-го рода |
b |
|
|
|
b |
|
|
|
|
ной при ..: |
f (x)dx |
lim |
f (x)dx . |
|||
|
|
a |
|
|
|
0 a |
|
|
49. |
Интегральное исчис- |
Раздел математического анализа, в котором |
||||||
|
ление |
изучаются понятия интеграла, его свойства и |
||||||
|
|
методы вычислений. |
|
|
|
|||
50. |
Интегрирование |
Операция нахождения неопределенного инте- |
||||||
|
|
грала для заданной функции. |
|
|||||
51. |
Касательная прямая |
Касательной к линии в точке M называется |
||||||
|
|
предельное положение секущей MN , когда |
||||||
|
|
точка N кривой неограниченно приближается |
||||||
|
|
к точке M . |
|
|
|
|
|
|
52. |
Квадратная матрица |
Матрица, состоящая из равного числа строк и |
||||||
|
|
столбцов. |
|
|
|
|
|
|
53. |
Коллинеарные век- |
Векторы, лежащие на одной прямой или на па- |
||||||
|
торы |
раллельных прямых. |
|
|
|
|||
54. |
Компланарные век- |
Векторы, лежащие в одной плоскости или па- |
||||||
|
торы |
раллельные ей. |
|
|
|
|
|
|
55. |
Комплексное число |
Выражение вида z |
x |
iy , где x, |
y – действи- |
|||
|
|
тельные числа, а i |
– мнимая единица. |
|||||
|
|
Величина x – действительная часть, y – |
||||||
|
|
мнимая часть. |
|
|
|
|
|
|

№ |
Термин |
|
|
|
Значение |
|
|
||
п/п |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
56. |
Конъюнкция |
Высказывание A |
B , |
которое истинно только |
|||||
|
|
в том случае, когда истинны оба высказывания |
|||||||
|
|
A и B . Конъюнкция |
A |
B соответствует ло- |
|||||
|
|
гической связке «и». |
|
|
|
|
|||
57. |
Критическая точка |
Точка, в которой производная функции равна |
|||||||
|
|
нулю или не существует. |
|
|
|
||||
58. |
Левая тройка векто- |
Тройка некомпланарных векторов a , b , c , |
|||||||
|
ров |
приведенных к общему началу, называется ле- |
|||||||
|
|
вой, если из конца вектора c |
видно, что крат- |
||||||
|
|
чайший поворот от вектора a к вектору b |
|||||||
|
|
происходит по часовой стрелке. |
|
||||||
59. |
Левосторонний пре- |
|
lim f (x) |
lim f (x) |
f (a |
0) . |
|||
|
дел функции |
|
x |
a |
x a |
0 |
|
|
|
|
|
x |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|||||||
60. |
Линейная алгебра |
Важная в приложениях часть алгебры, изуча- |
|||||||
|
|
ющая векторы, векторные пространства, ли- |
|||||||
|
|
нейные отображения и системы линейных |
|||||||
|
|
уравнений. |
|
|
|
|
|
||
61. |
Линейное дифферен- |
Дифференциальное уравнение вида |
|
||||||
|
циальное уравнение |
|
|
y a(x) y |
f (x) , |
|
|||
|
1-го порядка |
где функция a(x) называется коэффициентом |
|||||||
|
|
ЛДУ, а функция |
f (x) |
– правой частью (или |
|||||
|
|
свободным членом). |
|
|
|
|
|||
|
|
Если |
правая часть |
f (x) 0 , то |
уравнение |
||||
|
|
называется линейным однородным диффе- |
|||||||
|
|
ренциальным уравнением (ЛОДУ) первого |
|||||||
|
|
порядка. |
|
|
|
|
|
|
|
|
|
Если |
f (x) 0 , то уравнение |
называется ли- |
|||||
|
|
нейным неоднородным дифференциальным |
|||||||
|
|
уравнением (ЛНДУ) первого порядка. |
|||||||

№ |
Термин |
|
|
|
Значение |
|
|
|
|
||
п/п |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
62. |
Линейное дифферен- |
Дифференциальное уравнение вида |
|
|
|
|
|||||
|
циальное уравнение |
|
|
y |
p(x) y |
q(x) y f (x) , |
|
|
|
||
|
2-го порядка |
где функции |
p(x) , q(x) называются коэффи- |
||||||||
|
|
циентами уравнения, а функция |
f (x) |
|
– пра- |
||||||
|
|
вой частью (или свободным членом). |
|
|
|
||||||
|
|
Если правая часть |
f (x) 0 , то |
уравнение |
|||||||
|
|
называется линейным однородным диффе- |
|||||||||
|
|
ренциальным уравнением (ЛОДУ) второго |
|||||||||
|
|
порядка. |
|
|
|
|
|
|
|
|
|
|
|
Если f (x) |
0 , то уравнение называется ли- |
||||||||
|
|
нейным неоднородным дифференциальным |
|||||||||
|
|
уравнением (ЛНДУ) второго порядка. |
|
|
|
||||||
63. |
Линия второго по- |
Множество точек на плоскости, координаты |
|||||||||
|
рядка |
которых |
удовлетворяют |
уравнению |
|
второй |
|||||
|
|
степени |
|
|
|
|
|
|
|
|
|
|
|
|
Ax2 |
Bxy Cy2 Dx Ey F 0 . |
|||||||
64. |
Логарифмическая |
Логарифмической |
производной функции |
||||||||
|
производная |
y f (x) |
называется |
производная |
от |
ln y по |
|||||
|
|
переменной x , т.е. (ln y)x |
(ln y) y |
yx |
|
yx |
. |
||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|||||||||
65. |
Логические операции |
В качестве основных обычно называют отри- |
|||||||||
|
|
цание, конъюнкция, дизъюнкция, импликация, |
|||||||||
|
|
эквивалентность. |
|
|
|
|
|
|
|||
66. |
Логические связки |
Союзы «и», «или», «если…., то», «тогда и |
|||||||||
|
|
только тогда, когда» и частица «не». |
|
|
|
||||||
67. |
Математический |
Совокупность разделов математики, посвя- |
|||||||||
|
анализ |
щѐнных исследованию функций и их обобще- |
|||||||||
|
|
ний методами дифференциального и инте- |
|||||||||
|
|
грального исчислений. |
|
|
|
|
|
||||
68. |
Матрица |
Прямоугольная |
таблица |
|
|
чисел |
|||||
|
|
|
a11 |
a12 |
a1n |
|
|
|
|
|
|
|
|
A |
a21 |
a22 |
a2n |
, состоящая из m строк и |
|||||
|
|
|
|
|
|||||||
|
|
|
am1 am2 |
amn |
|
|
|
|
|
|
|
|
|
n столбцов. |
|
|
|
|
|
|
|
||

№ |
Термин |
|
|
Значение |
|
|
п/п |
|
|
|
|
||
|
|
|
|
|
|
|
69. |
Минор |
Минором |
Mij |
элемента aij |
определителя |
|
|
|
называется определитель, полученный из дан- |
||||
|
|
ного определителя вычеркиванием i -ой строки |
||||
|
|
и j -ого столбца, на пересечении которых сто- |
||||
|
|
ит элемент aij . |
|
|
|
|
|
|
|
|
|||
70. |
Мнимая единица |
Число i , обладающее свойством i2 |
1. |
|||
71. |
Мнимая часть |
См. комплексное число |
|
|
||
72. |
Многочлен |
Функция |
вида |
Pn (x) a0 xn |
a1xn 1 |
... an , |
|
|
где n |
– степень многочлена, a0 , a1, ..., an |
|||
–коэффициенты многочлена.
73.Множество Совокупность некоторых объектов, объеди-
|
|
ненных по какому-либо признаку в единое. |
|||||||||||||||||||
74. |
Модуль вектора |
Длина отрезка |
|
a |
|
, |
|
AB |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
75. |
Модуль комплексно- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
x |
iy |
|
r |
|
|
|
|
|
x2 y2 – |
длина |
радиус- |
|||||||
|
|
|
|
|
|
|
|||||||||||||||
|
го числа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вектора |
|
OM |
|
|
(x, y) соответствующей точки |
|||||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
M (x, y) в комплексной плоскости.. |
|
|||||||||||||||||
|
|
|
|
|
|||||||||||||||||
76. |
Монотонная функция |
Функция, которая либо убывает, либо возрас- |
|||||||||||||||||||
|
|
тает. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
77. |
Начальные условия |
Дополнение к дифференциальному уравнению, |
|||||||||||||||||||
|
|
задающие поведение его решения в начальной |
|||||||||||||||||||
|
|
точке. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
78. |
Неограниченная по- |
Последовательность {yn } называется неогра- |
|||||||||||||||||||
|
следовательность |
ниченной, если для любого положительного |
|||||||||||||||||||
|
|
числа A найдется хотя бы один элемент по- |
|||||||||||||||||||
|
|
следовательности yn , удовлетворяющий нера- |
|||||||||||||||||||
|
|
венству |
|
yn |
|
A. |
|
|
|||||||||||||
|
|
|
|||||||||||||||||||
79. |
Неопределенный ин- |
Совокупность всех первообразных для функ- |
|||||||||||||||||||
|
теграл |
ции f (x) : |
f (x)dx F (x) C . |
|
|||||||||||||||||
|
|
|
|||||||||||||||||||
80. |
Неправильная раци- |
Рациональная дробь, степень числителя кото- |
|||||||||||||||||||
|
ональная дробь |
рой не меньше степени знаменателя. |
|
||||||||||||||||||
81. |
Нулевой вектор |
Вектор 0 , модуль которого равен нулю. Нуле- |
|||||||||||||||||||
|
|
вой вектор направления не имеет. |
|
||||||||||||||||||
82. |
Область значений |
Множество всех значений, которые принимает |
|||||||||||||||||||
|
|
функция y |
|
f (x) при всех значениях аргумен- |
|||||||||||||||||
|
|
та x из области определения. |
|
|
|||||||||||||||||
83. |
Область определения |
Множество значений аргумента x , |
при кото- |
||||||||||||||||||
|
|
рых существует функция y |
f (x) . |
|
|||||||||||||||||
