
080100Экономика(МатАнализ и ЛинАлгебра) / Линейная алгебра_080100_заоч_1_курс_экз_паспорт
.pdfАВТОНОМНАЯ НЕКОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ЦЕНТРОСОЮЗА РОССИЙСКОЙ ФЕДЕРАЦИИ «РОССИЙСКИЙ УНИВЕРСИТЕТ КООПЕРАЦИИ»
КАЗАНСКИЙ КООПЕРАТИВНЫЙ ИНСТИТУТ (ФИЛИАЛ)
УТВЕРЖДАЮ Проректор по учебной работе
Казанского кооперативного института (филиала) Российского университета кооперации
_____________А. М. Хуснутдинова «____»_________________20___г.
ЛИНЕЙНАЯ АЛГЕБРА
ТЕСТОВЫЕ ЗАДАНИЯ
Направление подготовки (специальность) 080100.62 «Экономика»
Составители: ________________________________А.В. Поташев
________________________________Е.В. Поташева
«___»_____________2013 г.
Тестовые задания обсуждены на заседании кафедры «Инженернотехнические дисциплины и сервис» «__»____________2013 г., протокол №__.
Заведующий кафедрой ___________________________ А.М. Мухаметшин
СОГЛАСОВАНО Начальник отдела менеджмента качества _______________ Д.Н. Алюшева
1
№ |
Наименование пункта |
Значение |
1. |
Кафедра |
Инженерно-технические |
|
|
дисциплины и сервис |
2. |
Автор – разработчик |
Поташев А.В., д.ф.-м.н., профессор |
|
|
Поташева Е.В., к.т.н., доцент |
3. |
Наименование дисциплины |
Линейная алгебра |
|
|
|
4. |
Общая трудоемкость по |
180 (1 курс) |
|
учебному плану |
|
5. |
Вид контроля (нужное |
Предварительный (входной), |
|
подчеркнуть) |
текущий, промежуточный |
|
|
(экзамен) |
6. |
Для специальности(ей)/ |
080100.62 «Экономика» |
|
направления(й) подготовки |
нормативный срок и СПО |
|
|
заочная форма обучения |
7. |
Количество тестовых |
|
|
заданий всего по дисциплине, |
275 |
|
из них |
|
8. |
Количество заданий при |
20 |
|
тестировании студента |
|
|
|
|
9. |
Из них правильных ответов |
|
|
(в %): |
|
10. |
для оценки «отлично» |
85 % и больше |
|
|
|
11. |
для оценки «хорошо» |
70 % - 85% |
|
|
|
12. |
для оценки |
50% - 70% |
|
«удовлетворительно» |
|
|
или для получения оценки |
55% |
|
«зачет» не менее |
|
13. |
Время тестирования (в |
45 |
|
минутах) |
|
2
Содержание |
|
|
Стр. |
V1: МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ................................................................... |
4 |
V2: Формулы вычисления определителей........................................................ |
4 |
V2: Определители второго порядка .................................................................. |
6 |
V2: Определители третьего порядка............................................................... |
10 |
V2: Линейные операции над матрицами ........................................................ |
12 |
V2: Произведения матриц ................................................................................ |
17 |
V2: Ранг матрицы.............................................................................................. |
23 |
V2: Обратная матрица....................................................................................... |
25 |
V2: Системы линейных уравнений ................................................................. |
28 |
V2: Метод Крамера решения систем линейных уравнений ......................... |
30 |
V2: Метод Гаусса решения систем линейных уравнений ............................ |
34 |
V1: ВЕКТОРНАЯ АЛГЕБРА ............................................................................... |
41 |
V2: Линейные операции над векторами ......................................................... |
41 |
V2: Скалярное, векторное и смешанное произведения векторов. ............... |
44 |
V1: АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ............................. |
47 |
V2: Прямоугольные координаты на плоскости ............................................. |
47 |
V2: Полярные координаты на плоскости ....................................................... |
49 |
V2: Прямая на плоскости ................................................................................. |
53 |
V2: Кривые второго порядка............................................................................ |
64 |
V1: АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ......................... |
70 |
V2: Прямоугольные координаты в пространстве. ......................................... |
70 |
V2: Плоскость и прямая в пространстве......................................................... |
70 |
V1: КОМПЛЕКСНЫЕ ЧИСЛА............................................................................ |
75 |
V2: Комплексные числа и их представление. ................................................ |
75 |
V2: Операции над комплексными числами.................................................... |
80 |
3

F1: Линейная алгебра экзамен 1 курс 2013/2014 F2: Поташев А.В., Поташева Е.В.
F3: Тестовые задания по направлению подготовки 080100.62 «Экономика» заочная нормативный срок и СПО 275 задания, 20 вопросов, 180 часов F4: Дидактическая единица; Раздел; Тема
V1: Матрицы и определители
V2: Формулы вычисления определителей
I:
S: Формула вычисления определителя третьего порядка |
содержит |
следующие произведения: … |
|
+: |
|
-: |
|
-: |
|
+: |
|
I: |
|
S: Формула вычисления определителя третьего порядка |
содержит |
следующие произведения: … |
|
+: |
|
-: |
|
+: |
|
-: |
|
I: |
|
S: Формула вычисления определителя третьего порядка |
содержит |
следующие произведения: … |
|
+: |
|
+: |
|
-: |
|
-: |
|
I: |
|
4

S: Формула вычисления определителя третьего порядка |
содержит |
следующие произведения: … |
|
+: |
|
+: |
|
-: |
|
-: |
|
I: |
|
S: Формула вычисления определителя третьего порядка |
содержит |
следующие произведения: … |
|
+: |
|
-: |
|
-: |
|
+: |
|
I: |
|
S: Формула вычисления определителя третьего порядка |
содержит |
следующие произведения: … |
|
-: |
|
-: |
|
+: |
|
+: |
|
I: |
|
S: Формула вычисления определителя третьего порядка |
содержит |
следующие произведения: … |
|
-: |
|
+: |
|
+: |
|
-: |
|
5

I:
S: Формула вычисления определителя третьего порядка |
содержит |
|
следующие произведения: … |
|
|
+: |
|
|
+: |
|
|
-: |
|
|
-: |
|
|
V2: Определители второго порядка |
|
|
I: |
|
|
S: Определитель |
равен 0, если равно … |
|
-: 2 |
|
|
-: – 4 |
|
|
-: 0 |
|
|
+: 1 |
|
|
I: |
|
|
S: Определитель |
равен … |
|
-: 0 |
|
|
-: |
|
|
+: 1 |
|
|
-: |
|
|
I: |
|
|
S: Установите соответствие между матрицей и ее определителем.
L1:
L2:
L3:
R4: 480
R5: – 20
R3: 0
R1: – 7
R2: – 40
I:
6
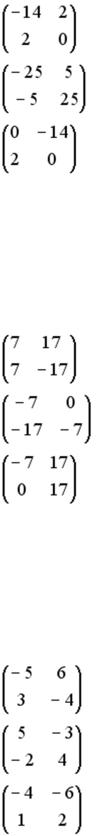
S: Установите соответствие между матрицей и ее определителем.
L1:
L2:
L3: R1: – 4
R2: – 600 R3: 28 R4: – 28 R5: 0
I:
S: Установите соответствие между матрицей и ее определителем.
L1:
L2:
L3:
R1: – 238
R4: – 49
R2: 49
R5: 119
R3: – 119
I:
S: Установите соответствие между матрицей и ее определителем.
L1:
L2:
L3:
R5: 12
R2: 14
R3: – 2
R4: – 14
R1: 2
7
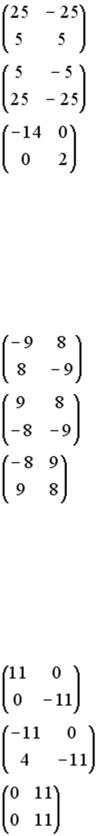
I:
S: Установите соответствие между матрицей и ее определителем.
L1:
L2:
L3: R1: 250 R2: 0
R4: – 125
R3: – 28
R5: 28
I:
S: Установите соответствие между матрицей и ее определителем.
L1:
L2:
L3: R1: 17 R2: – 17
R3: – 145
R4: 145
R5: 155
I:
S: Установите соответствие между матрицей и ее определителем.
L1:
L2:
L3:
R1: – 121
R2: 121
R3: 0
R4: 125
8

R5: 11
I:
и значениями
и значением определителя
R4: 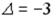
R5: 
R6: 
I:
S: Установите соответствие между величиной 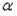 и значением определителя
и значением определителя
.
L1: 
L2: 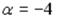
L3: 
L4: 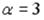
R1: 
R2: ∆= -8 R3: 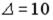
9

соответствие между величиной 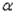 и значением определителя
и значением определителя
.
соответствие между величиной 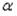 и значением определителя
и значением определителя
R1:  R2:
R2: 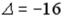 R3:
R3:  R4:
R4:  R5:
R5:  R6:
R6: 
V2: Определители третьего порядка
I:
−3 1 2 S: Вычислить определитель A = 0 4 0 −2 3 5
+: -44 I:
10
