080100Экономика(МатАнализ и ЛинАлгебра) / Линейная алгебра_080100_заоч_1_курс_экз_паспорт
.pdf
+: (7; – 1; – 1) -: (– 7; 1; 1) -: (7; 0; 0)
I:
S: |
. Тогда |
-: -: +: -: I:
S: |
имеет |
вид
+:
-:
-:
-: I:
S: |
при |
значениях
-:
-:
+: -: I:
S: |
равен … |
-:
-:
+: arccos
1
3
2
-: I:
71
S: Координата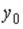 
точки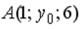 
, принадлежащей плоскости 
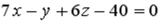, равна…
-: 5 +: 3 -: 4 -: 2 I:
S: Координата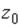 
точки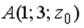 
, принадлежащей плоскости 
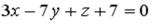, равна…
-: 7 -: 10 -: 13 +: 11 I:
S: Координата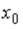 
точки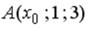 
, принадлежащей плоскости 
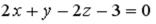, равна…
-: 5 -: 3 -: 6 +: 4 I:
S: Координата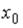 
точки 
, принадлежащей плоскости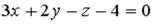 
, равна…
+: 2 -: 3 -: 4 -: 1 I:
S: Координата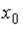 
точки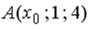 
, принадлежащей плоскости 
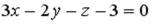, равна…
-: 4 -: 1 -: 2 +: 3 I:
72
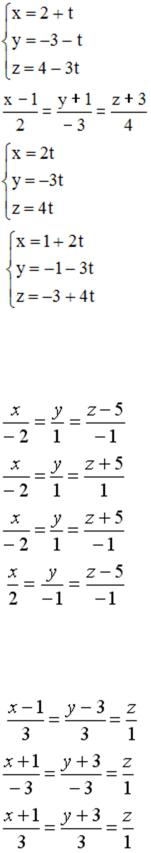
S: Параметрические уравнения прямой в пространстве, проходящей через
точку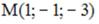 
перпендикулярно плоскости 
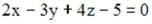, имеют вид …
-:
-:
-:
+:
I:
S: Уравнение прямой, проходящей через точку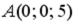 
перпендикулярно плоскости 
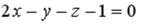, имеет вид…
-:
-:
-:
+:
I:
S: Уравнение прямой, проходящей через точку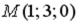 
перпендикулярно плоскости 
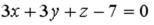, имеет вид…
+:
-:
-:
73
-: |
|
|
I: |
|
|
S: |
через точку |
перпендикулярно |
|
, имеет вид… |
|
-: |
|
|
-: |
|
|
-: |
|
|
+: |
|
|
I: |
|
|
S: |
через точку |
перпендикулярно |
|
имеет вид… |
|
-: |
|
|
-: |
|
|
-: |
|
|
+: |
|
|
I: |
|
|
S: |
пересекает плоскость |
в |
том |
|
|
+: |
|
|
-: |
|
|
-: |
|
|
-: |
|
|
I: |
|
|
S: |
и плоскость |
|
|
m и С, равных … |
|
-: |
|
|
+: |
|
|
74
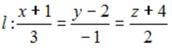и плоскость
в пространстве. Тогда прямая l … кости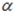 
плоскости 
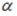кости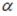 
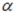под некоторым острым углом
и плоскостью
…
плоскости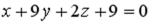 
с осью 
является …
V1: Комплексные числа
V2: Комплексные числа и их представление.
I:
S: Модуль комплексного числа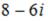 
равен …
-: 2 -: 14 +: 10
-: 
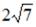I:
75
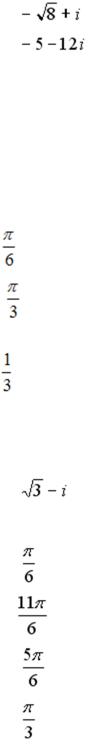
S: Установите соответствие между комплексным числом и его модулем
L1: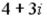 
L2: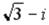 
L3:
L4:
R1: 5
R2: 2
R3: 3
R4: 13
R5: 7
I:
S: Аргумент комплексного числа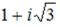 
равен …
-:
+: -: 2
-:
I:
S: Установите соответствие между комплексным числом и его аргументом
L1: 
L2:
L3: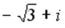 
R1:
R2:
R3:
R4:
I:
S: Установите соответствие между комплексным числом и его аргументом
L1: 1 + i L2: −1 + i L3: 1 − i
76
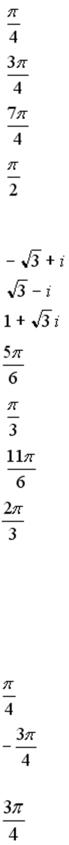
R1:
R2:
R3:
R4:
I:
S: Установите соответствие между комплексным числом и его аргументом
L1:
L2:
L3:
R1:
R3:
R2:
R4:
I:
S: Установите соответствие между комплексным числом и его аргументом
L1: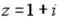 
L2: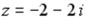 
L3: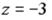 
R1:
R2:
R3: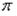 
R4:
I:
77
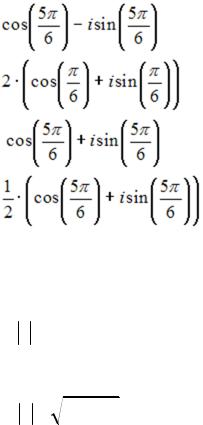
S: Комплексное число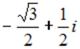 
в тригонометрической форме имеет вид …
-:
-:
+:
-:
I:
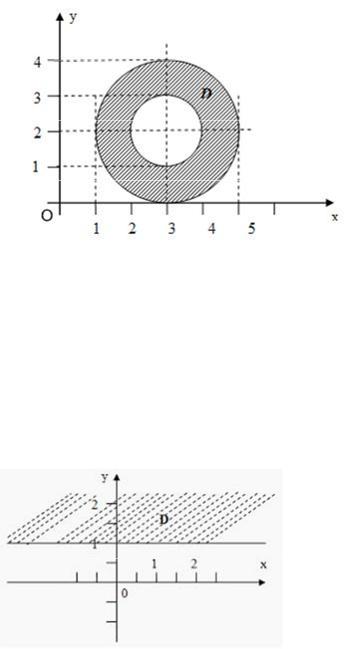
S: Задано комплексное число z=x+iy. Установите соответствие: L1: Re z
L2: Im z L3: z
R1: Re z = x
R2: Im z = y
R3: z = 
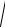x2 + y2
R4: Re z = y
R5: Im z = x
I:
S: Тригонометрическая форма записи комплексного числа имеет вид: +: z = r(cos ϕ + i sin ϕ)
-: zn = r n (cos nϕ + i sin nϕ) -: z = x + iy
-: z = reiϕ
I:
S: Показательная форма записи комплексного числа имеет вид: -: z = r(cos ϕ + i sin ϕ)
-: zn = r n (cos nϕ + i sin nϕ) -: z = x + iy
+: z = reiϕ
I:
S: Алгебраическая форма записи комплексного числа имеет вид: -: z = r(cos ϕ + i sin ϕ)
-: zn = r n (cos nϕ + i sin nϕ) +: z = x + iy
78
-: z = reiϕ
I:
S: Установите соответствие между формой записи комплексного числа и названием:
L1: z = r(cos ϕ + i sin ϕ) L2: z = x + iy
L3: z = reiϕ
R1: тригонометрическая R2: алгебраическая R3: показательная
R4: степенная
I:
S: Все точки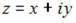 
комплексной плоскости, принадлежащие множеству D, изображённому на рисунке,
удовлетворяют условию …
-: 
-: 
-: 
+: 
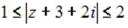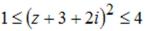
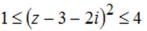
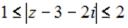I:
S: Все точки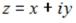 
комплексной плоскости, принадлежащие множеству D, изображённому на рисунке,
79
удовлетворяют условию …
плоскости, принадлежащие множеству
числами.
уравнения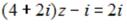 
, то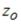 
равно …
выражение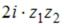 
равно …
-: 
-: 
-: 
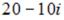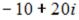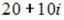I:
S: Значение выражения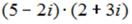 
равно …
-: 
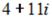
80