
080100Экономика(МатАнализ и ЛинАлгебра) / Лекции_Математический анализ
.pdf
4.4.5. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
4.4.5.1. Вид ЛОДУ второго порядка с постоянными коэффициентами, его решение, характеристическое уравнение
ЛОДУ второго порядка с постоянными коэффициентами называется ДУ вида
y′′ + py′ + qy = 0 , |
(57) |

 где p, q – постоянные.
где p, q – постоянные.
Согласно теореме о виде общего решения ЛОДУ (см. п. 4.4.3.2) общее решение этого уравнения имеет вид y(x) = C1 y1 (x) + C2 y2 (x) , где y1 (x) , y2 (x) – линейно независимые частные решения. Рассмотрим теперь вопрос о виде этих решений.
Теорема. |
Функция y = ekx , где k – корень квадратного уравнения |
|
|
k2 + pk + q = 0 , |
(58) |
является решением ЛОДУ (57).
Уравнение (58) называется характеристическим уравнением ЛОДУ (57)
.
Так как характеристическое уравнение является квадратным уравнением, то оно имеет два корня, причем в зависимости от величины дискриминанта
D = p2 − 4q возможны три случая:
D > 0 : k1 ≠ k2 – различные действительные корни;
D = 0 : k1 = k2 = k – совпадающие действительные корни (кратные корни);
D < 0 : k1,2 =(p ± i −D )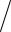 2 =α ± iβ – комплексно сопряженные корни.
2 =α ± iβ – комплексно сопряженные корни.
Рассмотрим, какой вид имеет общее решение ЛОДУ (57) в каждом из перечисленных случаев.
4.4.5.2. Общее решение ЛОДУ при k1 ≠ k2 , k1,2 R
Теорема. Если характеристическое уравнение (58) имеет различные действительные корни k1 ≠ k2 , то общее решение ЛОДУ (57) имеет вид
121

y =C ek1x + C ek2x . |
(59) |
|
1 |
2 |
|
Пример. Найти общее решение ЛОДУ y′′ + y′ − 6 y = 0 .
Составим характеристическое уравнение, решим его и найдем общее решение ЛОДУ:
k2 + k − 6 = 0 k1 = 2, k2 = −3 y =C1e2x + C2e−3x .
4.4.5.3. Общее решение ЛОДУ при k1 = k2 = k R
Теорема. Если характеристическое уравнение (58) имеет кратный действительный корень k1 = k2 = k , то общее решение ЛОДУ (57) имеет вид
y = ekx (C + C |
2 |
x). |
(60) |
||
|
|
1 |
|
|
|
Пример. Найти общее решение ЛОДУ y′′ − 4 y′ + 4 = 0 . |
|||||
Составим характеристическое уравнение, решим его и найдем общее ре- |
|||||
шение ЛОДУ: |
|
|
|
|
|
k2 − 4k + 4 = 0 k = k |
2 |
= 2 y = e2x (C + C x) . |
|||
1 |
|
|
1 |
2 |
|
4.4.5.4. Общее решение ЛОДУ при k1,2 = α ± iβ C |
|
||||
Теорема. Если характеристическое |
|
уравнение |
|
(58) имеет |
комплексно-сопряженные корни |
k1,2 = α ± iβ, то общее решение ЛОДУ (57) имеет вид |
|
|
|
||
y = eαx (C cosβx + C sinβx) . |
(61) |
||||
1 |
|
|
2 |
|
|
Пример. Найти общее решение ЛОДУ y′′ − 2 y′ + 2 = 0 .
Составим характеристическое уравнение, решим его и найдем общее решение ЛОДУ:
k 2 − 2k + 2 = 0 k1,2 |
|
2 ± 4 − 8 |
|
2 ± 2i |
α =1 |
|
|
= |
= |
=1 ± i |
β =1 |
|
|||
|
|
2 |
|
2 |
|
|
|
y = ex (C1 cos x + C2 sin x) .
4.4.6.Линейные неоднородные дифференциальные уравнения второго
порядка с постоянными коэффициентами
4.4.6.1. ЛНДУ второго порядка с постоянными коэффициентами
ЛНДУ второго порядка с постоянными коэффициентами называется уравнение
122
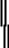
y′′ + py′ + qy = f (x) , |
(62) |
где p=const, q=const, f (x) ≡/ 0 .
Как было показано в пункте 4.4.4.2, общее решение ЛНДУ (62) имеет вид (56), где Y (x) – общее решение соответствующего ему ЛОДУ (57), а y(x) – не-
которое частное решение ЛНДУ (62). Отысканию функции Y (x) был посвящен предыдущий пункт 4.4.5. Ниже приведем метод подбора частного решения
y(x) по виду правой части f (x) . |
|
4.4.6.2. Частное решения ЛНДУ с правой частью вида |
f (x) =eλx P (x) |
|
n |
Пусть f (x) =eλx P (x) , где λ – действительное число, а |
P (x) – многочлен |
n |
n |
степени n. Например: |
|
f (x) = x2e−3x n = 2, |
λ = −3; |
f (x) = 2x + 3 n =1, |
λ = 0; |
f (x) = 4e5x n = 0, |
λ = 5. |
В зависимости от того, с каким количеством корней k1 , k2 характеристи-
ческого уравнения совпадает число λ получается различный вид частного ре-
шения y(x) :
λ ≠ k |
, λ ≠ k |
2 |
|
y(x) =Q (x)eλx , где |
Q (x) |
– многочлен степени n |
|
1 |
|
|
n |
n |
|
|
|
с неопределенными |
|
пока коэффициентами. |
Например, |
Q0 (x) = A, |
|||
Q (x) = A + Bx |
Q (x) = A + Bx + Cx2 , … |
|
||||
1 |
|
2 |
|
|
|
|
λ = k , λ ≠ k |
2 |
|
y(x) = xQ (x)eλx , |
|
||
1 |
|
|
|
n |
|
|
λ = k = k |
2 |
|
|
y(x) = x2Q (x)eλx . |
|
|
1 |
|
|
|
n |
|
|
Из сравнения всех этих трех случаев видно, что вид частного решения |
||||||
ЛНДУ в рассмотренном случае можно описать единой формулой |
|
|||||
|
|
|
|
|
y(x) = xrQ (x)eλx , |
(63) |
|
|
|
|
|
n |
|
где r – количество корней характеристического уравнения, с которыми совпадает число λ.
Для того, чтобы найти само частное решение, необходимо определить значения неопределенных коэффициентов, входящих в многочлен Qn (x) . Для
123

этого функцию (63) необходимо подставить в уравнение (62) и найти такие значения коэффициентов, чтобы уравнение обратилось в тождество.
Пример. Найти общее решение ЛНДУ y′′ + y′ = x .
Составим характеристическое уравнение, найдем его корни и запишем общее решение соответствующего ЛОДУ:
k2 + k = 0 k1 = 0, k2 = −1 Y (x) =C1 + C2e−x . 1) По правой части уравнения определим величины n и λ:
f (x) = x = x1e0x n =1, λ = 0 .
2)Сравним корни характеристического уравнения со значением λ и запишем вид частного решения:
λ= k1, λ ≠ k2 r =1, y(x) = xQ1(x)e0x = x(A + Bx) = Ax + Bx2 .
3)Определим постоянные A и B, для этого найдем первую и вторую производные функции y(x) и подставим их в левую часть уравнения:
y′ = A + 2Bx, y′′ = 2B 2B + A + 2Bx = x .
Чтобы полученное равенство было тождеством необходимо, чтобы оно выполнялось при любых значениях переменной x. Это будет выполнено, если коэффициенты при одинаковых степенях x в обеих частях равенства будут равны:
x1 : 2B =1 |
B =1 / 2, A = −1 |
y(x) = |
x |
2 |
− x . |
|
x0 |
: 2B + A = 0 |
|
|
|||
|
2 |
|
||||
4) Запишем теперь общее решение ЛНДУ:
y(x) =C1 + C2e−x + x22 − x .
4.4.6.3. Частное решения |
ЛНДУ с |
правой |
частью вида |
f (x) = eλx (M cosωx + N sin ωx) |
|
|
|
Пусть теперь f (x) = eλx (M cosωx + N sin ωx) , |
где λ, ω, |
M, N – действи- |
|
тельные числа. Например: |
|
|
|
f (x) = e2x sin x |
ω=1, |
λ = 2; |
|
f (x) = 3cos2x |
ω= 2, |
λ = 0; |
|
f (x) = e−x (4cos x − 2sin x) ω=1, |
λ = −1. |
|
|
|
124 |
|
|
Вид частного решения y(x) зависит от того, совпадает или нет пара комплексно сопряженных чисел λ ± iω с корнями характеристического уравнения:
λ ± iω≠ k1,2 y(x) = eλx (Acosωx + Bsin ωx) , где A, B – неопределен-
ные пока коэффициенты.
λ ± iω= k = α ± iβ |
y(x) = xeλx (Acosωx + Bsin ωx) . |
|
1,2 |
|
|
Из этих двух случаев видно, что вид частного решения ЛНДУ можно опи- |
||
сать единой формулой |
|
|
y(x) = xr eλx (Acosωx + Bsin ωx) , |
(64) |
|
где r – количество пар корней характеристического уравнения, с которыми совпадает пара чисел λ ± iω.
Для того, чтобы найти само частное решение, также необходимо определить значения неопределенных коэффициентов A и B. Для этого функцию (64) необходимо подставить в уравнение (62) и найти значения коэффициентов, обращающих его в тождество.
Пример. Найти общее решение ЛНДУ y′′ + 4 y = cos3x .
Составим характеристическое уравнение, найдем его корни и запишем общее решение соответствующего ЛОДУ:
k 2 + 4 = 0 k1,2 = ±2i Y (x) = C1 cos 2x + C2 sin 2x . 1) По правой части уравнения определим величины ω и λ:
f (x) = cos3x ω = 3, λ = 0 .
2)Сравним корни характеристического уравнения со значением λ ± iω и запишем вид частного решения:
λ ± iω= ±3i
k1,2 = ±2i λ ± iω≠ k1,2 r = 0, y(x) = Acos3x + Bsin3x .
3)Определим постоянные A и B, для этого найдем первую и вторую производные функции y(x) и подставим их в левую часть уравнения (62):
y′ = −3Asin 3x + 3B cos3x, y′′ = −9 Acos3x − 9B sin 3x .
−9Acos3x − 9Bsin 3x + 4Acos3x + 4Bsin 3x = cos3x .
125
Чтобы полученное равенство было тождеством необходимо, чтобы оно выполнялось при любых значениях переменной x. Это будет выполнено, если коэффициенты при cos3x и при sin 3x в обеих частях равенства будут равны:
cos3x : −5A =1 A = −1 / 5, |
B = 0 y(x) = −cos3x . |
||
sin3x : −5B = 0 |
|
|
5 |
4) Запишем теперь общее решение ЛНДУ: |
|||
y(x) = C |
cos2x + C |
2 |
sin 2x − cos3x . |
1 |
|
5 |
|
|
|
|
|
126

РАЗДЕЛ IV. РЯДЫ
Тема 5. Числовые ряды
5.1.Знакоположительные ряды
5.1.1.Числовой ряд, его сходимость, сумма ряда
5.1.1.1.Бесконечные суммы
Прежде, чем ввести понятие числового ряда рассмотрим один пример, показывающий необходимость осторожного обращения с суммами, имеющими бесконечное число слагаемых.
Возьмем бесконечную сумму
S=1 −1 +1 −1 +1 −1 +…
ипопробуем найти ее значение.
Если воспользоваться свойством ассоциативности сложения, то искомую бесконечную сумму можно записать в различных видах, например:
1)S =(1−1) + (1−1) + (1−1) +…;
2)S =1 + (−1+1) + (−1+1) + (−1+1) +…;
3)S =1−(1−1+1−1+1−1+…) .
Впервом случае получим S = 0 , во втором – S =1, а в третьем S = 12 , так
как из вида 3) следует равенство S =1 − S .
Из приведенного примера видно, что свойства бесконечных сумм существенно отличаются от свойств обычных (конечных) сумм.
5.1.1.2. Определение числового ряда
Пусть дана бесконечная последовательность чисел u1 , u2 , u3 , …, un , ….
Выражение вида
∞
u1 + u2 + u3 +…+ un +…= ∑un
n=1
127


 называется числовым рядом, числа u1 , u2 , u3 , … – членами ряда, un – общим или n-м членом ряда.17
называется числовым рядом, числа u1 , u2 , u3 , … – членами ряда, un – общим или n-м членом ряда.17
Задание ряда равносильно заданию его общего члена в виде функции от порядкового номера n: un = f (n) .
Пример. Ряд с общим членом un = 1n будет иметь вид
∞ |
|
|
|
|
|
+…+ |
|
+…. |
∑1 |
=1 + |
1 |
+ |
1 |
1 |
|||
1 |
n |
|
2 |
|
3 |
|
n |
|
Этот часто встречающийся ряд принято называть гармоническим рядом.
5.1.1.3. Частичная сумма ряда
Сумма конечного числа первых N членов ряда называется N-й частичной
суммой ряда:
|
|
N |
|
|
S1 = u1 , S2 = u1 + u2 , S3 = u1 + u2 + u3 , SN = ∑un . |
|
|||
Пример. Рассмотрим ряд |
|
n=1 |
|
|
|
|
|
||
∞ |
1 |
|
(65) |
|
|
|
|||
∑n=1 n(n +1) |
||||
|
||||
и найдем его частичные суммы. Для этого представим сначала его общий член в виде
un = n(n1+1) = 1n − n 1+1 .
Тогда
|
|
S |
= u |
=1 − 1 , S |
2 |
= u |
+ u |
2 |
=1 − 1 |
+ 1 − 1 =1 − 1 , |
|
|
|||||||
|
|
1 |
|
|
1 |
|
2 |
|
1 |
2 |
2 |
3 |
|
3 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
S |
3 |
= u + u |
2 |
+ u =1 − 1 |
+ |
1 − 1 + |
1 − 1 =1 − 1 S |
N |
=1 − |
1 |
. |
||||||||
|
|||||||||||||||||||
|
1 |
|
|
3 |
2 |
|
|
2 |
3 |
3 4 |
4 |
|
|
N +1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
5.1.1.4. Сходимость ряда и его сумма
Ряд называется сходящимся, если последовательность его N-х частичных сумм SN при неограниченном росте номера N стремится к конечному пределу:
17 Двойной вертикальной чертой слева абзаца будем отмечать основные определения.
128

lim SN = S .
N →∞

 Число S при этом называется суммой ряда.
Число S при этом называется суммой ряда.
Пример. Рассмотрим ряд (65). Его частичная сумма равна SN =1 − |
1 |
|
. |
||||||||
N +1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
Тогда S = lim |
SN |
|
|
|
1 |
=1. Следовательно, ряд (65) сходится, а его |
|||||
= |
lim 1 |
− |
|
|
|||||||
|
|||||||||||
N →∞ |
|
|
N →∞ |
|
N +1 |
|
|
|
|
||
сумма равна 1.
Если N-я частичная сумма SN ряда при неограниченном росте номера N
не стремится к конечному пределу, то ряд называется расходящимся.
5.1.1.5. Ряд бесконечной геометрической прогрессии
Рассмотрим ряд, составленный из членов геометрической прогрессии
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a + aq + aq2 +…+ aqn−1 |
+…= ∑aqn−1 , a ≠ 0 , |
|
|
(66) |
|||||||||
и исследуем его сходимость. |
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Так как N-я частичная сумма этого ряда при |
q ≠1 равна |
SN = |
a(1 − qN ) |
, |
|||||||||||||||||||||
1 |
− q |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
то рассмотрим следующие случаи. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1) |
|
|
q |
|
|
|
|
|
<1. Тогда lim qN = 0 и, следовательно, |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
N →∞ |
|
a(1 − qN ) |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
lim SN = S = lim |
= |
|
|
|
. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 − q |
1 |
− q |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
N→∞ |
N→∞ |
|
|
|
|
|
|
||||||
Значит ряд (66) сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2) |
|
q |
|
|
|
>1. Тогда lim qN |
= ∞ и, следовательно, |
|
lim SN не существует, то |
||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
N →∞ |
|
|
|
|
|
|
|
N →∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
есть ряд расходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
При |
|
q |
|
=1 возможны еще два случая. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
3) q =1. Тогда SN = Na , |
lim SN |
= lim Na = ∞. Ряд расходится. |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
N →∞ |
N →∞ |
|
|
|
|
|
|
|
|
|
|
|
4) q = −1. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a, N − нечетное, |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
SN = a − a + a − a +…+ (−1)N a = |
N |
− четное. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
129 |
|
|
|
|
|
|
|
|
|
|
|

Таким образом, четные и нечетные частичные суммы постоянны, но имеют
различные значения, следовательно lim SN не существует и ряд расходится.
N →∞
Таким образом, ряд геометрической прогрессии (66) сходится при q <1 и
расходится при q ≥1.
5.1.2.Действия над сходящимися рядами
5.1.2.1.Умножение ряда на число
Теорема 3. Если ряд
|
∞ |
|
|
|
∑un |
(67) |
|
|
n=1 |
|
|
сходится и имеет сумму S , то ряд |
|
|
|
|
∞ |
|
|
|
∑aun , |
(68) |
|
|
n=1 |
|
|
где a – заданное число, тоже сходится и его сумма Q равна aS .18 |
|||
Доказательство. Пусть SN – N-я частичная сумма ряда (67), а QN – N-я |
|||
частичная сумма ряда (68). Тогда имеем равенство |
|
||
N |
|
|
N |
QN = ∑aun = au1 + au2 +…+ auN = a(u1 + u2 +…+ uN ) = a∑un = aSN . |
|||
n=1 |
|
|
n=1 |
Перейдя к пределу при N → ∞, получим |
|
||
Q = lim QN |
= lim aSN |
= a lim SN = aS .■19 |
|
N →∞ |
N →∞ |
N →∞ |
|
Следствием доказанной теоремы является утверждение, что если ряд (67) расходится, то при a ≠ 0 ряд (68) также расходится.20
Вывод. При умножении ряда на число a ≠ 0 его сходимость не изменяет-
ся.
18Двойными толстыми вертикальными чертами слева и справа абзаца будем отмечать формулировки теорем.
19Знак ■ читается так: «Что и требовалось доказать».
20Попробуйте доказать это утверждение самостоятельно, используя метод доказательства от противного.
130
