
080100Экономика(МатАнализ и ЛинАлгебра) / Лекции_Математический анализ
.pdf
Далее дифференцируя производные второго порядка получаются производные третьего порядка и т.д.
Разных производных n -го порядка будет (n +1).
2.4.4. Производная функции по направлению
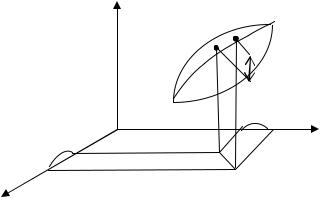
Рассмотрим функцию трех переменных u (x, y, z). Возьмем в простран-
стве точку M и исходящий из нее луч . На луче выберем точку M1 . Обо-
значим MM1 = .
M1
M
|
|
|
РИС. 2.4.2 |
|
Определение: Производной по направлению от функции |
||||
u = u(x, y, z) называется предел |
||||
∂u |
= |
lim |
u(M1 )−u(M ) |
. |
|
||||
∂ |
|
|||
|
→0 |
|||
Обозначение производной по направлению ∂∂u .
Производная |
∂u - это скорость изменения функции u в точке M по |
||||||
|
∂ |
|
|
|
|
|
|
направлению l . |
|
|
|
|
|
|
|
Если направление |
совпадает с положительным направлением коорди- |
||||||
натной оси Ox , то |
∂u совпадают с частной производной ∂u и т.п. |
|
|||||
|
∂ |
|
|
|
|
∂x |
|
Пусть направление |
характеризуется направляющими |
косинусами |
|||||
cosα, cosβ, cos γ. Тогда можно показать, что |
|
|
|||||
|
∂u = |
∂u cosα + |
∂u |
cosβ + |
∂u cos γ . |
(5) |
|
|
|
||||||
|
∂l |
∂x |
|
∂ y |
∂l |
|
|
|
|
|
41 |
|
|
||

2.4.5. Градиент
Градиентом функции u (x, y, z) называется вектор
gradu = ∂∂ux i + ∂∂uy j + ∂∂uz k .
2.4.5.1. Свойства градиента и производной по направлению |
|
||||||||||||||||||||||||||
1. Производная по направлению |
∂u в фиксированной точке |
M равна |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
||||
проекции grad u в этой точке на направление . |
|
|
|
|
|
|
|||||||||||||||||||||
2. Наибольшее и наименьшее значения производной по направлению в |
|||||||||||||||||||||||||||
данной точке |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
max |
|
∂u |
= |
|
|
gradu |
|
, min ∂u = − |
|
gradu |
|
. |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример. Найти |
наибольшую |
скорость |
возрастания |
функции |
|||||||||||||||||||||||
u = x2 + y2 + z2 в точке M (1,1,1). |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Найдем gradu в точке M |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
∂u (M )= 2x |
|
M |
= 2; ∂u (M )= 2y |
|
|
M = 2; ∂u (M )= 2z |
|
|
M = |
2 , |
|
||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
∂x |
|
|
|
|
|
∂y |
|
|
∂z |
|
|
|
|
|
|
||||||||||||
|
|
|
|
gradu |
M = 2i + 2 j + 2k . |
|
|
|
|
|
|
||||||||||||||||
По второму свойству градиента наибольшее значение |
∂u |
равно |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
max ∂u |
|
|
= |
|
gradu (M ) |
|
= |
4 + 4 + 4 = 2 |
3 . |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
∂ |
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2.4.6. Полное приращение, полный дифференциал функции двух переменных
2.4.6.1. Полное приращение функции двух переменных
Рассмотрим функцию двух переменных z = f (x, y). Для независимых пе-
ременных x, y зададим приращения x, y.
42
Полным приращением |
функции z = f (x, y) называется |
разность |
|
z = f (x + x, y + y) − f (x, y) |
|
|
|
Геометрический смысл |
z. Полное приращение функции |
z = f (x, y) - |
|
это приращение ординаты z, соответствующее приращениям x, |
y |
аргумен- |
|
тов x, y. |
|
|
|
|
z |
f (x + x, y + y) |
|
f (x, y) |
|
|
|
z |
|
y |
|
x |
(x, y) |
y |
|
(x + |
x, y + y) |
Пример. z = x y , |
z =(x + x)(y + y)− xy = x y + y x + x y. |
|
Полное приращение функции z = f (x, y) зависит от четырех переменных
x, y, x, y..
|
Теорема. Если функция |
z = f (x, y) |
имеет непрерывные частные произ- |
|
водные fx′(x, y)и fy′(x, y), то полное приращение функции равно |
||||
|
z = fx′(x, y) |
x + fy′(x, y) |
y + α x +β y, |
|
где |
бесконечно |
малые величины α |
и β зависят от x, y то есть |
|
lim α = 0, lim β = 0. |
|
|
||
x→0 |
x→0 |
|
|
|
y→0 |
y→0 |
|
|
|
Данная формула называется формулой приращения функции z = f (x, y).
2.4.6.2. Полный дифференциал функции двух переменных
Полным дифференциалом функции z = f (x, y) в точке (x, y) называется
выражение
dz = fx′(x, y) x + fy′(x, y) y
и обозначается dz или df .
43

Теорема. Если функция z = f (x, y) обладает непрерывными частными производными в точке (x, y), то дифференциал обладает следующими свой-
ствами: |
|
|
|
|
|
|
1) |
dz линейно зависит от |
x, |
y. |
|
|
|
2) |
Полный дифференциал dz |
отличается от полного приращения |
z на |
|||
бесконечно |
малую величину |
более высокого |
порядка малости, |
чем |
||
ρ= ( |
x)2 + ( |
y)2 . |
|
|
|
|
Благодаря свойствам (1), |
(2) |
дифференциал dz |
называется главной ли- |
|||
нейной частью приращения z. |
|
|
|
|
||
Определение. Функция z = f (x, y), имеющая непрерывные частные про- |
||||||
изводные ∂z , |
∂z называется дифференцируемой. |
|
|
|||
|
∂x |
∂y |
|
|
|
|
Новая формулировка понятия дифференцируемости демонстрирует качественные изменения, которые возникают при переходе от одной переменной к двум.
2.4.6.3. Вторая форма записи полного дифференциала
Приращения независимых переменных x и y равны дифференциалам
независимых переменных dx, dy.
Тогда выражение полного дифференциала имеет вид
dz = fx′(x, y)dx + fy′(x, y)dy.
При малых приращениях x, y полное приращение дифференцируемой функции z можно приближение заменить дифференциалом dz
f (x + x, y + y)− f (x, y)≈ fx′(x, y) x + fy′(x, y) y.
Отсюда получается формула для приближенных вычислений: f (x + x, y + y)≈ f (x, y)+ fx′(x, y) x + fy′(x, y) y.
44

2.4.7. Частные производные высших порядков
Частные производные ∂∂xz и ∂∂yz функции двух переменных z = f (x, y)
также являются функциями двух переменных и их можно продифференцировать по x ипо y. Тогда получаются 4 производных второго порядка.
∂∂z = ∂x ∂x
∂∂z = ∂y ∂y
∂2 z = zxx′′ ∂x2
∂2 z = z′′yy ∂y2
|
∂ |
∂z |
= |
|
∂2 z |
= z′′yx . |
|||||
|
|
|
|
|
|
|
|
|
|
||
|
|
∂y∂x |
|||||||||
∂y |
∂x |
|
|
||||||||
|
∂ |
|
|
|
|
∂ |
2 |
z |
|
||
|
|
∂z |
= |
|
|
= z′′xy . |
|||||
|
|
|
∂x∂y |
||||||||
|
∂x |
∂y |
|
|
|
||||||
Производные |
|
∂2 z |
и |
∂2 z |
|
называются смешанными. |
|
|
|
|
|||||||||||||||||||||
|
∂x∂y |
∂y∂z |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Теорема. Если смешанные производные второго порядка непрерывны, то |
|||||||||||||||||||||||||||||||
они равны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
z = e |
xy |
; |
|
∂z |
= ye |
xy |
; |
∂z |
= xe |
xy |
; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
∂x |
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
∂2 z |
= y |
2 |
e |
xy |
; |
∂2 z |
= x |
2 |
e |
xy |
; |
|
|
|
∂2 z |
= e |
xy |
+ xye |
xy |
; |
∂2 z |
= e |
xy |
+ xye |
xy |
. |
|||||
∂x2 |
|
|
∂y2 |
|
|
|
|
∂x∂y |
|
|
∂y∂x |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Различных производных второго порядка только 3.
Далее дифференцируя производные второго порядка получаются производные третьего порядка и т.д.
Пример.
z = x3 y2 + 5x; zx′ = 3x2 y2 + 5; z′y = 2x3 y; |
|
|
||||||||||
′ |
|
|
2 |
′′ |
2 |
|
′′ |
3 |
; |
|
|
|
zxx = 6xy |
|
; zxy = 6x |
|
y; zyy = 2x |
|
|
|
|
||||
′′ |
6 y |
2 |
′′′ |
|
|
′′ |
|
′′ |
= 6x |
2 |
. |
|
zxxx = |
|
|
; zxyx =12xy; |
zyyy = 0; |
zxyy |
|
||||||
Разных производных третьего порядка будет 4, а равных производных n -
го порядка будет (n +1).
∂n z |
; |
∂n z |
; |
∂n z |
; |
∂n z |
. |
||
∂xn |
∂xn−1∂y′ |
∂xn−2 |
∂y2 |
∂yn |
|||||
|
|
|
|
||||||
45

2.4.8.Производные сложных функций
2.4.8.1.Дифференцирование сложной функции от одной переменной с двумя промежуточными.
Пусть z = f (u,v). Здесь u,v − промежуточные функции, зависящие от
x : u =u(x),v = v(x). |
|
|
Функции |
|
z = f (u,v); |
u =u (x) |
и v = v(x) −дифференциру- |
|||||||||||||||||||||||||||||
емы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда |
z = f (u(x)), v(x)). является сложной функцией от одной незави- |
|||||||||||||||||||||||||||||||||||
симой переменной x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Необходимо найти производную |
dz . |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
||
Для отыскания |
dz |
|
используется формула полного приращения |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = |
∂z |
|
u + ∂z |
v + α u + β v; |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂u |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂v |
|
|
|
|
|
|
|
|
|
|
||||||
α,β−бесконечно малые при |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Далее |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
z |
= |
|
∂z |
|
|
|
u |
+ |
∂z |
|
|
v |
+ α |
u |
+ β |
|
v |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
∂v |
|
|
|
|
x |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
∂u |
|
|
|
|
x |
|
|
x |
|
|||||||||||||||
в пределе при |
|
|
x → 0 получим |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
dz = lim |
|
z |
= |
|
|
∂z |
lim |
|
z |
+ |
∂z |
lim |
|
v |
|
+ |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
∂v |
|
x |
|
|
|
|
||||||||||||||||||||||
dx |
x→0 |
|
x |
|
∂u |
|
x→0 |
x |
|
|
x→0 |
|
|
|
|
|
||||||||||||||||||||
+ lim α |
|
lim |
|
|
|
u |
+ |
|
lim β |
|
lim |
|
v |
= |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
x→0 |
|
|
x→0 |
|
|
x |
|
x→0 |
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= |
∂z |
|
du |
+ ∂z |
|
dv |
+ 0 du |
+ 0 dv . |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
dx |
dx |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
∂u |
|
∂v |
|
|
|
|
|
|
dx |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Следовательно,
dxdz = ∂∂uz dudx + ∂∂vz dxdv
для функции z = f (u,v) u = u(x), v = v(x).
Пример.
46
|
x2 |
|
|
|
′ |
|
|
|
|
|
|
|
2 |
|
z =(sin 0) , |
|
|
|
|
|
|
|
|
. |
|||||
zx − ? Пусть u =sin x, v = x |
|
|||||||||||||
Тогда z = u |
v |
. |
|
∂z |
= u |
v−1 |
v; |
∂z |
= u |
v |
ln u |
|
|
|
|
|
∂u |
|
∂u |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
dz = vuv−1 cos x + uv ln u 2x = x2 (sin x)x2 −1 + (sin x)x2 ln (sin x) 2x. |
||||||||||||||
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.4.8.2. Дифференцирование сложной функции двух переменных с двумя |
||||||||||||||
промежуточными. |
|
|
|
|
|
|
|
|
||||||
Пусть z = f (u,v). |
Здесь |
u,v − промежуточные функции, зависящие от |
||||||||||||
двух независимых переменных x, y. |
|
Тогда z = f (u(x, y)), v(x, y)) является |
||||||||||||
сложной функцией от двух переменных x, y. |
|
|
||||||||||||
∂z ∂z
Необходимо найти частные производные ∂x ; ∂y .
Чтобы найти ∂∂xz , фиксируется y и используется формула из предыдуще-
го случая, т.к. функции u,v зависят уже только от x (необходимо лишь обык-
новенные производные заменить на частные). Получим
|
|
|
|
∂z |
= |
|
∂z |
|
∂u |
+ |
∂z |
|
∂v |
|
|
|
|
|
|
|
|
|
∂x |
|
∂u |
∂x |
∂v |
∂x |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Аналогично вычисляется |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
= |
|
∂z |
|
∂u |
+ |
∂z |
|
∂v |
|
|
|
||
|
|
|
|
∂y |
|
|
∂u |
|
|
∂y |
|
∂v |
|
∂y |
|
|
|
|
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти ∂z , |
∂z |
при x = 0, |
y = 0, z = 2uv + u −3v, u = ex−y , v = x2 + y2 |
|||||||||||||||
|
∂x |
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
= (2v +1)ex−y + (2u − |
3) 2x; |
|
|
|
|
|
|
|
|
||||||||
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
= (2v +1)ex−y (−1)+ ( |
2u − 3) 2 y; |
∂z |
|
x=0 =1; |
∂z |
|
x=0 = −1. |
||||||||||
|
|
|||||||||||||||||
∂y |
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
y=0 |
∂y |
|
y=0 |
|
47
2.4.8.3. Частный случай сложной функции от одной переменной с двумя промежуточными.
Пусть z = f (x, y), y = y(x). Здесь x играет роль и независимой и проме-
жуточной переменной. Поэтому промежуточных переменных две: x, y. Незави-
симая переменная одна – x.
|
Тогда dz = |
∂z + |
∂z |
dy . |
|
|
|
|
|||
|
dx |
∂x |
∂y |
|
dx |
|
|
|
|
||
|
Следует различать |
∂z −частную производную функции z = f (x, y) и |
|||||||||
|
|
|
|
|
∂x |
|
|
|
|
||
dz −производную сложной функции |
y = f (x, y(x)) |
с учетом не только непо- |
|||||||||
dx |
|
|
|
|
|
|
|
|
|
|
|
средственного вхождения x, но и того, что y также зависит от x. |
|
||||||||||
|
Пример. |
|
|
|
|
|
|
|
|
|
|
|
z = x2 y2 − x − y, y |
= ln x, dz |
|
x = l |
− ? |
|
|
|
|||
|
|
|
|
|
|||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
dz |
|
|
|
1 |
|
dz |
1 |
1 |
||
|
dx = (2xy2 −1)+ |
(2x2 y −1) x ; y(l )=1; dx = 2l |
−1 + (2l2 −1) l |
= 4l − l −1. |
|||||||
2.4.9. Экстремумы функции двух переменных |
|
|
|||||||||
|
Рассмотрим функцию двух переменных z = f (x, y). |
|
|||||||||
|
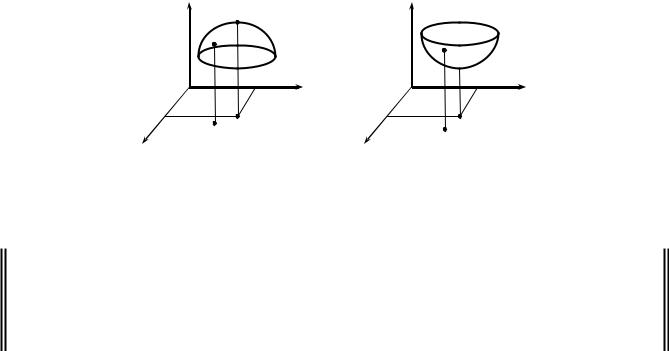
1. Точка M0 (x0 , y0 ) |
называется точкой максимума функции z = f (x, y) , |
|||||||||
если |
f (x, y)< f (x0 , y0 ) |
для любой точки |
M (x, y) |
из некоторой окрестности |
|||||||
точки M 0 (Рис. 2.3). |
|
|
|
|
|
|
|
|
|
||
|
2. Точка M1(x1, y1) называется точкой минимума функции |
z = f (x, y) , |
|||||||||
если |
f (x, y) > f (x1, y1 ) |
для любой точки |
M (x, y) |
из некоторой окрестности |
|||||||
точки M1 (Рис. 2.4). |
|
|
|
|
|
|
|
|
|
||
48
z |
z |
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
y0 |
y |
|
|
O |
|
y1 |
y |
|
|
|
|
|
|
|
x0 |
|
|
|
|
|
|
|
|
x1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
M0(x0,y0) |
|
|
|
M1(x1,y1) |
|
|||||||
|
|
|
|
|
|
|
|
M(x,y) |
|
|
|
M(x,y) |
|
|||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
РИС. 2.3 |
|
|
|
|
РИС. 2.4 |
|
|
|||||||
2.4.9.1. Необходимое условие существование экстремума |
|
|||||||||||||||||||||
Теорема. |
|
Необходимое условие экстремума. Если в точке M 0 (x0 , y0 ) |
||||||||||||||||||||
функция z = f (x, y) имеет экстремум, то частные производные ∂z , |
∂z в точке |
|||||||||||||||||||||
M 0 обращаются в нуль или не существуют. |
|
|
|
∂x |
∂y |
|||||||||||||||||
|
|
|
|
|
||||||||||||||||||
Доказательство. |
Пусть |
|
|
y = y0 . Тогда |
z = f (x, y0 ) |
– функция одной пере- |
||||||||||||||||
менной x . По условию теоремы эта функция при x = x0 |
достигает экстремума и |
|||||||||||||||||||||
равна f (x0 , y0 ) . |
Необходимое условие экстремума для функции одной пере- |
|||||||||||||||||||||
менной |
|
– |
|
|
это |
равенство |
нулю |
или |
|
не |
существование |
производной, т.е. |
||||||||||
fx′(x, y0 ) |
|
x=x |
= 0 |
или |
fx′(x, y0 ) |
|
x=x |
не существует. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
Но |
|
fx′(x0 , y0 ) является в то же время частной производной по x от f (x, y) |
||||||||||||||||||||
в точке M |
0 |
(x , y |
0 |
) . Следовательно, ∂z |
|
x=x |
= 0 или не существует. Аналогично |
|||||||||||||||
|
||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y=y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
можно доказать, что |
∂z |
|
|
x=x |
= 0 или не существует. |
|
|
|
||||||||||||||
|
|
|
|
|||||||||||||||||||
∂ y |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
y=y0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
Следует отметить, что указанное условие не является достаточным, т.е. из |
||||||||||||||||||||||
условий |
|
fx′(x0 , y0 ) = 0 и |
|
fy′(x0 , y0 ) = 0 не следует, что M 0 (x0 , y0 ) является точ- |
||||||||||||||||||
кой экстремума. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Точка |
M 0 (x0 , y0 ) , |
|
в которой частные производные функции |
z = f (x, y) |
||||||||||||||||||
обращаются в нуль ( fx′(x0 , y0 ) = 0 , fy′(x0 , y0 ) = 0 ) или не существуют, называ-
ется критической.
49

Замечание. Критические точки не обязательно являются точками экстремума.
Пример 1. Рассмотрим функцию z = −x2 + y2 . В точке O(0,0) частные про-
′ |
′ |
|
изводные zx = −2x , |
zy = 2y обращаются в нуль. Однако точка O не является |
|
точкой экстремума. |
|
|
Геометрически в этой точке поверхность имеет сед- |
z |
|
лообразную форму (Рис. 2.5). На кривой сечения этой по- |
O |
|
верхности плоскостью yOz точка O является самой низ- |
y |
|
|
||
кой точкой. На кривой сечения поверхности плоскостью |
x |
|
xOz точка O – самая высокая точка. |
РИС. 2.5 |
|
Точки, подобные точке O , называются точками минимакса или седло-
выми точками.
2.4.9.2. Достаточные условия существования экстремума функции двух переменных
Эти условия носят более сложный характер, чем для функции одной переменной, и приводятся без доказательства.
Пусть M 0 (x0 , y0 ) – критическая точка функции z = f (x, y) . Далее иссле-
дуем выражение
|
∂2 z |
∂2 z |
∂2 z |
|
2 |
|||
= |
∂x2 |
|
∂y2 |
|
− |
|
. |
|
|
||||||||
|
|
|
|
∂x∂y |
|
|||
1. Если (M0 )> 0, то z = f (x, y) имеет в точке M 0 экстремум.
Причем, если ∂2 z (M0 ) > 0 , то M 0 – точка минимума;
∂x2
если ∂2 z (M0 ) < 0 , то M 0 – точка максимума.
∂x2
2. Если (M0 ) < 0 , то точка M 0 – не является точкой экстремума (сед-
ловая точка);
3. Если (M 0 ) = 0 , то заключение о характере точки сделать нельзя,
необходимо дополнительное исследование. 50
