Глава 2. Комбинаторика

Комбинаторикой называется раздел дискретной математики, который занимается следующими вопросами:

1. Задача перечисления: найти количество элементов заданной математи- ческой модели.

1. Задача перебора: построить алгоритм перебора этих элементов.

Основное внимание мы будем уделять задаче перечисления.

Конечная математическая модель в комбинаторике называется конфигурацией. Мы изучим следующие конфигурации: размещения, сочетания, разбиения и их обобщения. Для дальнейшего изучения рекомендуем [9], [10], [14].

§2.1. Размещения

Дано n предметов и m ящиков, в которые размещаются предметы. Сколько существует размещений, удовлетворяющих некоторым заданным условиям?

Определение 1. Размещением с повторениями называется функция

f: {x₁, x₂, , x_m} { y₁,y₂, ,y_n } .

Элементы x_i называются предметами, а y_j  ящиками.

Число всех размещений с повторениями равно количеству последовательностей {a₁,a₂, , a_m} чисел 1a_in и значит оно равно n^m .

Определение 2. Рассмотрим некоторое конечное множество равнове-роятных элементарных событий, которые мы будем иногда назвать исхода-ми. Событием называется подмножество множества всех исходов. Его эле-менты называются благоприятными исходами. Вероятность события определяется как отношение количества благоприятных исходов к количеству всех исходов.

Например, если мы бросаем монету, то возможны два исхода. Число исходов выпадения «орла» равно 1. Значит, вероятность выпадения орла равно ½.

Упражнение 1. Бросают две кости. Найти вероятность выпадения 10 очков.

Решение. В данном случае число всех исходов равно 6². Благоприятные исходы: (4,6), (5,5), (6,4). Отсюда вероятность равна p=3/36=1/12.

Определение 3. Размещением называется произвольная инъекция

f: {x₁ , x₂ ,  , x_m} { y₁,y₂, ,y_n } .

(В каждый ящик размещают не более одного предмета.)

Теорема 1. Число размещений равно.

Доказательство. Первый предмет можно разместить n способами, второй – n-1, , m-й – n-m+1. Получаем .

Упражение 2. В группе m студентов. Найти вероятность того, что найдется два студента, родившиеся в один день.

Решение. Число всех вариантов 365^m. Число неблагоприятных вариантов равно , гдеn=365. Получаем . Ниже приводится таблица значений вероятности при различныхm:

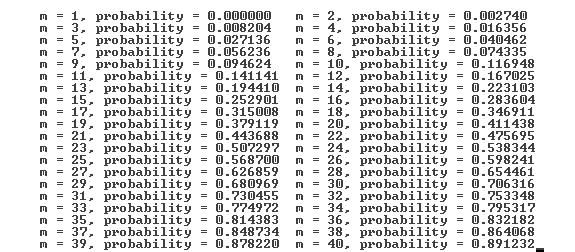
Например, если число студентов равно 23, то вероятность равна примерно 0.5

Определение 3. Пусть заданы m ящиков. Упорядоченным размещении-ем предметов a₁, a₂, , a_n называется указание последовательности предметов для каждого ящика, при котором каждый предмет участвует ровно один раз.

Пример 1. На рисунке 2.1 показаны упорядоченные размещения предметов a, b по трем ящикам.

ba ab a b a b b a ba

ab a b b a b a ba ab

Рис. 2.1. Упорядоченные размещения

Сначала размещается буква a в первый ящик и одним из четырех способов размещается b. Потом буква a размещается во второй ящик, в этом случае снова b размещается одним из четырех способов. Затем буква a размещается в третий ящик, буква b размещается одним из четырех способов. Всего получаем 12 упорядоченных размещений.

Теорема 2. Число [m]ⁿ упорядоченных размещений n предметов в m ящиков равно m(m+1) ∙ ∙ ∙ (m+n1).

Доказательство. После размещения первого предмета в таблицу одним из m способов

a1

∙ ∙ ∙

второй предмет может быть размещен одним из m+1 способов. Предположим, что уже размещено i1 предметов, и пусть при k=1, 2, …, m в k-м ящике находится r_k объектов. Тогда i-й объект может быть добавлен одним из (r₁ +1) + (r₂ +1) + ∙ ∙ ∙ + ( r_m +1) = i1+m способов. Отсюда число всех упорядоченных размещений будет равно m(m+1) ∙ ∙ ∙ (n1+ m).