Теорема 3. Хроматическая функция f(q) конечного графа  с n вершинами является многочленом степени  n.

Доказательство. По индукции по числу ребер m. При m=0 получаем f_(q)=qⁿ . Пусть граф имеет m+1 ребер (и n вершин). Выбросим произвольное ребро  . Получится граф ’, хроматическая функция которого – многочлен степени n согласно предположению индукции. Чтобы получить число раскрасок исходного графа , нужно из этого числа вычесть число раскрасок, при которых концы удаленного ребра  окрашены в одинаковый цвет. Это число раскрасок будет хроматической функцией графа ’’, полученного удалением ребра  и отождествлением концов этого ребра. Отсюда

f_(q)= f_’(q) – f_{ ’’} (q) – разность многочленов степени  n.

§4.4. Деревья

Дерево, имеющее n вершин, называется нумерованным, если каждой из его вершин присвоен индивидуальный номер k{1, 2, ,n}.

Теорема 1. (Кэли) Число нумерованных графов с n вершинами равно n^n-2.

Доказательство. Сопоставим каждому нумерованному дереву последовательность n-2 чисел принадлежащих {1, 2, ,n}. Эта последовательность называется кодом Прюфера и строится следующим образом. В цикле находится висячая вершина с наименьшим номером. Номер вершины смежной с найденной записывается в последовательность. Цикл повторяется n2 раза. Наоборот, по последовательности n чисел из {1, 2, ,n+2} можно построить нумерованное дерево с помощью следующих действий:

Выписываем множество B={1, 2, 3, ∙ ∙ ∙, n+2}. Устанавливаем начальное множество ребер дерева T= . Далее выполняются действия:

for (i=1; i<n1; i++)

{

b= min { kB: ka_j  j ≥ i} ;

добавить к T ребро {b,a_i} ;

B = B \ {b} ;

}

Число последовательностей из n-2 чисел принадлежащих множеству {1, 2, ∙ ∙ ∙, n} равно nn-2, значит число нумерованных деревьев равно nn-2.

Доказательство следующего утверждения можно найти в [3].

Теорема 2. Число максимальных поддеревьев связного графа равно абсолютной величине алгебраического дополнения произвольного элемента матрицы

,

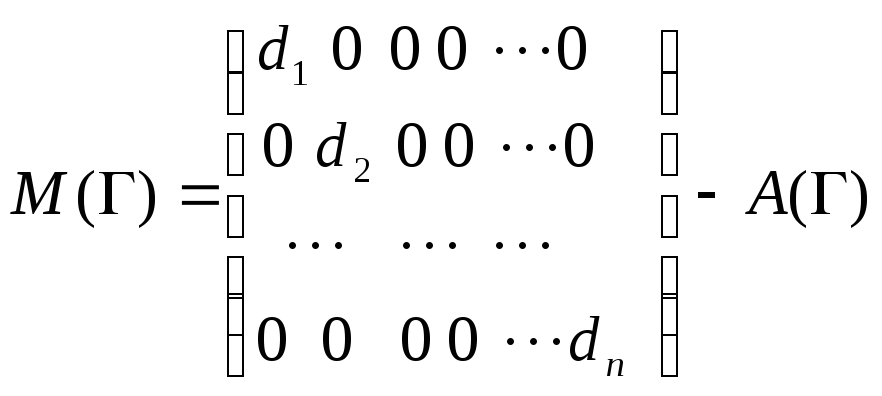где d_i – степени вершин графа , A() =( a_{i j} ) – матрица смежности

Пример 1. Рассмотрим граф , изображенный на рис. 4.4. Вычислим количество его максимальных поддеревьев.

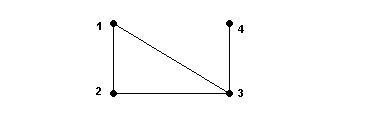
Рис. 4.4. Простой граф

Найдем матрицу M().

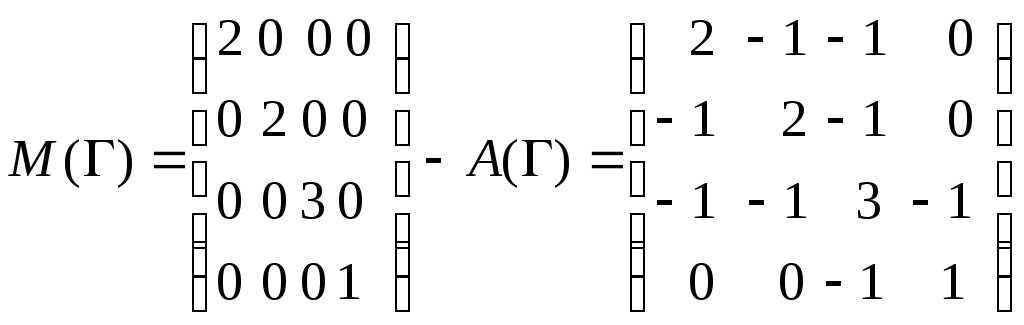
Отсюда число максимальных поддеревьев равно |A₃₁| = 3.

§4.5. Числа Каталана

Пусть =(V,E) – простой граф. Напомним, что две вершины, принадлежащие одному ребру, называются смежными. Элементарным путем длины n в графе  , соединяющим вершины p и q , называется последовательность вершин (v₀, v₁,   , v_n ) таких, что

• p=v₀ и q=v_n ;

• v_i и v_i+1 смежны , i{0,1,   , n1};

• v_i =v_j  i=j .

Элементарным циклом длины n в графе  называется последовательность вершин (v₀, v₁,   , v_n ) таких, что

• v₀ =v_n ;

• v_i и v_i+1 смежны , i{0,1,   , n1};

• v_i =v_j  ( i=j  {i,j}={0,n} ) .

Элементарный цикл можно интерпретировать как непрерывный замкнутый путь в графе, не имеющий кратных вершин. Простой граф, не имеющий элементарных циклов длины >0, называется деревом. Дерево с выделенной вершиной называется корневым, а выделенная вершина – его корнем.

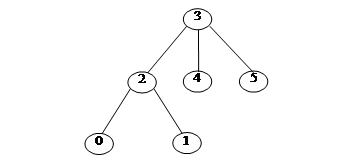
Рис. 4.5. Корневое дерево

Для каждой вершины q существует единственный элементарный путь, соединяющий ее с корнем. Длина этого пути называется высотой вершины q. Смежные с q вершины, высота которых больше высоты вершины q на 1, называются детьми вершины q. На рис. 4.5 показано дерево с корнем 3.

Определение 1. Корневое дерево, каждая вершина которого имеет не более двух детей, называется бинарным, если детям приписан дополнительный признак ‘левой’ или ‘правой’ смежной вершины. Вершина не может иметь две левые или две правые смежные вершины. Бинарное дерево вместе с функцией, сопоставляющей каждой вершине некоторое число, называется бинарным деревом чисел.

Бинарное дерево чисел можно определить по индукции:

1. Пустое дерево является бинарным деревом чисел.

2. Если T₁ и T₂ – бинарные деревья чисел, то (T₁, число, T₂) – бинарное дерево чисел.

Определим отношение эквивалентности на множестве бинарных деревьев чисел S~T следующим образом.

1. Если S=T=, то S~T.

2. Если S=(S₁, m, S₂), T=(T₁, n, T₂) , S₁~ T₁ и S₂~ T₂ , то S~T.

Число классов эквивалентности бинарных деревьев имеющих n вершин называется n-м числом Каталана и обозначается через c_n .

На рис. 4.6 показаны классы эквивалентности бинарных деревьев, имеющих n вершин, при n=0, 1, 2, 3:

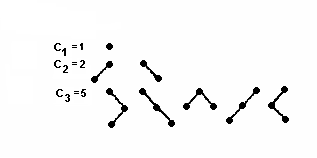
Рис. 4.6. Бинарные деревья.

Пример 1. Число расстановок скобок. Пусть ‘*’  бинарная операция на множестве A, которая не предполагается ни коммутативной, ни ассоциативной. Терм определяется по индукции. В нормальной форме Бэкуса-Наура определение будет следующим:

Терм ::= a | (Терм*Терм)

Здесь aA – произвольный элемент. Например, термами являются слова: (a*a)*b, a*(b*c), и т.д. Число термов, содержащих n операций *, равно c_n .

Изображенным на рисунке бинарным деревьям соответствуют термы:

1. a ,

2. (a*b) ,

3. ((a*b)*c), (a*(b*c)),

4. (a*((b*c)*d)), (a*(b*(c*d))), ((a*b)*(c*d)), (((a*b)*c)*d), ((a*(b*c))*d) .

Пример 2. Деревом поиска называется бинарное дерево, вершинам которого соответствуют элементы некоторого линейно упорядоченного множества. Причем для каждой вершины значение в ней не меньше значений в вершинах левого поддерева и больше значений в вершинах правого поддерева. Элементы возрастающей последовательности n чисел можно расположить в узлах дерева поиска . Оно будет бинарным деревом и может быть выбрано c_n способами.