Лемма 2. Пусть (V,e) – плоский конечный граф. Тогда существует вершина VV такая, что d(V)5. Здесь d(V) – степень вершины V.

Доказательство. Иначе 2q =  d(v)  6p, и q3p, а мы доказали раньше, что q  3p – 6.

Теорема 4. Для плоского связного графа существует правильная раскраска вершин в 5 цветов.

Доказательство. Для p5 теорема верна. Пусть для p – 1 вершин теорема доказана. Рассмотрим граф с p вершинами. Найдем в нем вершину v с d(v) 5. Обозначим через [v] подграф, полученный удалением вершины v и инцидентных ей ребер. Существует правильная раскраска графа [v]. Наша задача – раскрасить вершину v. Если d(v) < 5, то вершину v раскрасим цветом, которого нет у смежных с v вершин. Пусть d(v)=5 и пусть все смежные с v вершины раскрашены в различные цвета.

Обозначим через ₁₃ подграф графа [v], состоящий из вершин цвета 1 и 3. Если в нем нет путей между вершинами 1 и 3 из смежных с v, то компоненту связности вершины 3 перекрасим следующим образом: все вершины компоненты цвета 3 перекрасим в цвет 1, а все вершины компоненты цвета 1 – в цвет 3. Затем v покрасим в цвет 3. Если в графе ₁₃ существует путь, соединяющий вершины 1 и 3 и состоящий из вершин цвета 1 или 3, то в подграфе ₂₄ нет пути между вершинами, смежными с v. В этом случае перекрасим вершины компоненты содержащей 4, аналогично тому, как это делалось выше: цвета 2 – в 4, а цвета 4 – в 2. Таким образом, если граф имеет p вершин, то для него существует правильная раскраска пятью красками. Теорема доказана.

Платоновы тела. Многогранник, у которого грани имеют одинаковое число сторон, и в каждой вершине сходится одинаковое число ребер, называется правильным. Рис. 4.7 показывает, что по крайней мере 5 правильных многогранников существует. Следующее приложение эйлеровой характеристики – доказательство того, что правильные многогранники исчерпываются телами Платона.

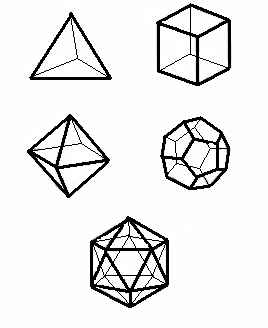
Рис. 4.7. Пять платоновых тел

Теорема 5. Пусть p – число вершин, q – число ребер, r – число граней правильного многогранника. Тогда возможен один из следующих случаев:

	p	q	r
Тетраэдр	4	6	4
Куб	8	12	6
Октаэдр	6	12	8
Додекаэдр	20	30	12
Икосаэдр	12	30	20

Доказательство. Вершины графа, состоящего из ребер и вершин фиксированного многогранника имеют одинаковую степень. Обозначим эту степень через x. Пусть y – число сторон грани этого многогранника. Получаем систему уравнений

.

Так как x,y  3, а в случае x,y  4 имеет место неравенство , то возможны следующие случаи:x=3 или y=3.

Рассмотрим случай x=3:

.

Получаем

x=3, y=3, ;

x=3, y=4, ;

x=3, y=5, .

Аналогично x=4 , x=5 при y=3.

§4.7. Упражнения Свойства графов

Все графы предполагаются простыми. Графы называются изоморфными, если существует биекция f между множествами их вершин, такая что {u,v} ребро  {f(u), f(v)} – ребро.

1. Доказать, что граф имеет четное число вершин с нечетными степенями.

2. При встрече студентов состоялось 15 рукопожатий, трое человек сделали по 4 рукопожатия, а другие – по 3. Сколько было студентов.

3. Может ли существовать группа из 23 человек, каждый из которых знаком с пятью другими?

4. В соревнованиях по шахматам по круговой системе участвуют 5 человек. Все, кроме Иванова и Петрова, сыграли различное число партий. Сколько партий сыграли Иванов и Петров?

5. Можно ли нарисовать без отрыва карандаша граф K₆, у которого удалено одно ребро.

6. Найти число попарно неизоморфных графов, у которых 2 вершины имеют степень 2, 2 вершины имеют степень 3, и 2 вершины имеют степень 4. Остальные вершины имеют степень 0.

7. Найти число попарно неизоморфных графов, у которых 3 вершины имеют степень 2, 3 вершины имеют степень 3, и 3 вершины имеют степень 4. Остальные вершины имеют степень 0.

8. Доказать, что в простом графе, имеющем не меьше двух вершин, всегда найдутся две вершины одинаковой степени.

9. Какие графы из следующих ниже изоморфны:

10. Какие графы из следующих ниже изоморфны:

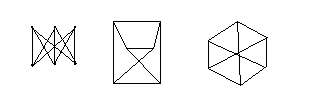
11. Найти число всех попарно неизоморфных графов, имеющих 4 вершины. Нарисовать эти графы.

Ответ: (см. рис.4.8) существует 11 неизоморфных графов

Рис. 4.8. Графы, имеющие 4 вершины

12. Кратчайший путь соединяющий вершины u и v в графе называется геодезическим путем между вершинами. Его длина обозначается d(u,v). Диаметром D() графа называется длина самого длинного геодезического пути в этом графе, т.е. D()=max{d(u,v): u,vV}. Найти диаметры графов

(1) K₅ ;

(2)

(3) Для дерева.

13. Матрица смежности состоит из коэффициентов a_ij=1  вершины i и j смежны.

(1) Построить матрицы смежности для графов K₃ и K₄ ;

(2) Доказать, что сумма коэффициентов i-й строки матрицы смежности равна степени i-й вершины;

(3) Построить матрицу смежности графа, состоящего из вершин и ребер куба.

(4) С помощью матрицы смежности построит матрицу, коэффициентами которой является количества путей длины 2 из вершины i в вершину j .

(5) Как связаны след матрицы A³ с числом треугольников в графе?

14. Циклы {z₁, z₂,    , z_n}называются независимыми, если z₁z₂    z_n   Доказать, что у связного графа максимальное число независимых циклов равно q-p+1.

15. Сколько компонент связности имеет лес, содержащий 76 вершин и 53 ребра?

16. Доказать, что среди 6 человек найдется тройка знакомых, или тройка незнакомых людей.

17. В компании, состоящей из пяти студентов, среди любых трех найдутся два знакомых и два незнакомых. Доказать, что компанию можно рассадить за круглым столом таким образом, что любые два соседа будут знакомы.