§6.1. Комбинаторные объекты

Задача 1. Найти количество элементов в указанном множестве

Варианты

1. Сколько подмножеств множества {1, 2, ... , 1000} не содержат чисел ни кратных 6 , ни кратных 4?

2. Сколько подмножеств множества {1, 2, ...., 1000} содержат по крайней мере одно число кратное 5 и ни одного – кратного 7 ?

3. Сколько существует подмножеств множества {1, 2, 3, ... , 1000} имеющих по крайней мере одно число, кратное трем или четырем.

4. Сколько подмножеств множества {1, 2, ... , 1000} не содержат ни одного нечетного числа, но имеют по крайней мере одно число кратное 7 ?

5. Сколько подмножеств из {1,2,3, …, 300} состоят из чисел, делящихся на 4, и не содержат ни одного числа, делящегося на 3?

6. Сколько подмножеств множества {1,2,3, … , 1000} содержат по крайней мере одно число кратное 4, но ни одного кратного 7?

7. Сколько подмножеств множества {1, 2, ... , 1000} не содержат чисел ни кратных 6 , ни кратных 15?

8. Сколько подмножеств множества {1, 2, ...., 1000} содержат по крайней мере одно число кратное 5 и ни одного – кратного 18 ?

9. Сколько существует подмножеств множества {1, 2, 3, ... , 1000} имеющих по крайней мере одно число, кратное 15 или 21.

10. Сколько подмножеств множества {1, 2, ... , 1000} не содержат ни одного нечетного числа, но имеют по крайней мере одно число кратное 21 ?

11. Сколько подмножеств из {1,2,3, …, 300} состоят из чисел, делящихся на 6, и не содержат ни одного числа, делящегося на 7?

12. Сколько подмножеств множества {1, 2, ... , 1000} не содержат чисел ни кратных 8 , ни кратных 6?

13. Сколько подмножеств множества {1, 2, ...., 1000} содержат по крайней мере одно число кратное 12 и ни одного – кратного 13 ?

14. Сколько существует подмножеств множества {1, 2, 3, ... , 1000} имеющих по крайней мере одно число, кратное 6 или 11.

15. Сколько подмножеств множества {1, 2, ... , 1000} не содержат ни одного нечетного числа, но имеют по крайней мере одно число кратное 17 ?

16. Сколько подмножеств из {1,2,3, …, 300} состоят из чисел, делящихся на 7, и не содержат ни одного числа, делящегося на 3?

17. Сколько подмножеств множества {1, 2, ... , 1000} не содержат чисел ни кратных 6 , ни кратных 9?

18. Сколько подмножеств множества {1, 2, ...., 1000} содержат по крайней мере одно число кратное 11 и ни одного – кратного 7 ?

19. Сколько существует подмножеств множества {1, 2, 3, ... , 1000} имеющих по крайней мере одно число, кратное 12 или 13.

20. Сколько подмножеств множества {1, 2, ... , 1000} не содержат ни одного нечетного числа, но имеют по крайней мере одно число кратное 23 ?

21. Сколько подмножеств из {1,2,3, …, 1000} состоят из чисел, делящихся на 7, и не содержат ни одного числа, делящегося на 12?

22. Сколько подмножеств множества {1, 2, ... , 1000} не содержат чисел ни кратных 6 , ни кратных 10?

23. Сколько подмножеств множества {1, 2, ...., 1000} содержат по крайней мере одно число кратное 12 и ни одного – кратного 7 ?

24. Сколько существует подмножеств множества {1, 2, 3, ... , 1000} имеющих по крайней мере одно число, кратное 11 или четырем.

25. Сколько подмножеств множества {1, 2, ... , 1000} не содержат ни одного нечетного числа, но имеют по крайней мере одно число кратное 11 ?

26. Сколько подмножеств из {1,2,3, …, 300} состоят из чисел, делящихся на 2, и не содержат ни одного числа, делящегося на 3?

27. Сколько подмножеств множества {1, 2, ... , 1000} не содержат чисел ни кратных 10 , ни кратных 4?

28. Сколько подмножеств множества {1, 2, ...., 1000} содержат по крайней мере одно число кратное 4 и ни одного – кратного 7 ?

29. Сколько существует подмножеств множества {1, 2, 3, ... , 1000} имеющих по крайней мере одно число, кратное 3 или 8.

30. Сколько подмножеств множества {1, 2, ... , 1000} не содержат ни одного нечетного числа, но имеют по крайней мере одно число кратное 5 ?

31. Сколько подмножеств множества {1, 2, ...., 1000} содержат по крайней мере одно число кратное 4 и ни одного – кратного 9 ?

32. Сколько существует подмножеств множества {1, 2, 3, ... , 1000} имеющих по крайней мере одно число, кратное 3 или 5.

33. Сколько подмножеств множества {1, 2, ... , 1000} не содержат ни одного нечетного числа, но имеют по крайней мере одно число кратное 15 ?

34. Сколько подмножеств из {1,2,3, …, 300} состоят из чисел, делящихся на 4, и не содержат ни одного числа, делящегося на 7?

35. Сколько подмножеств множества {1, 2, ... , 1000} не содержат чисел ни кратных 12 , ни кратных 9?

36. Сколько подмножеств множества {1, 2, ...., 1000} содержат по крайней мере одно число кратное 12 и ни одного – кратного 7 ?

Примеры решения задачи 1.

Пример 1.

Сколько подмножеств множества A={1, 2, ...., 1000} содержат ни чисел кратных 8, ни чисел кратных 12 ?

Решение.

Для произвольного действительного числа x обозначим через [x] его целую часть. (Например [2.5]=2, [1/2]=0, [3]=3.) Пусть 12A – подмножество множества A состоящее из чисел кратных 12, A\12A  A – подмножество чисел не кратных 12. Элементы, не кратные ни 12 ни 8, составляют множество (A\12A)\8A. Нам нужно найти число подмножеств этого множества. Поскольку число элементов этого множества равно

|(A\12A)\8A|=|A\(12A8A)|=|A|-|12A8A |=

|A|-|12A|-|8A |+|НОК(12,8)A|=1000-[1000/12]-[1000/8]+[1000/24],

то количество его подмножеств равно

Ответ:

Пример 2.

Сколько подмножеств множества A={1, 2, ...., 1000} содержат по крайней мере одно число кратное 8 и ни одного – кратного 12 ?

Решение.

Пусть 12A – подмножество множества A состоящее из чисел кратных 12, A\12A  A – подмножество чисел не кратных 12. Элементы, не кратные ни 12 ни 8, составляют множество (A\12A)\8A.

Каждое подмножество из A\12A может быть одного из следующих типов:

1. оно не содержит ни одного элемента кратного 8,

2. оно содержит хотя бы один элемент, кратный 8.

Отсюда количество подмножеств множества A\12A равно сумме количеств подмножеств первого и второго типа. Подмножества первого типа – это в точности подмножества не содержащие ни элементов кратных 12, ни элементов, кратных 8. Нам нужно найти количество подмножеств второго типа.

Следовательно, искомое число равно

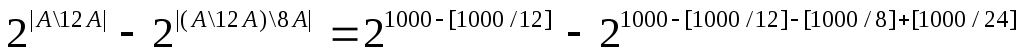
Ответ:

Пример 3.

Сколько подмножеств множества A={1, 2, ...., 1000} содержат по крайней мере одно число кратное 8 или 12 ?

Решение.

Каждое подмножество множества A обладает одним из следующих взаимоисключающих свойств:

1. оно не содержит ни чисел кратных 8, ни чисел кратных 12,

2. оно содержит по крайней мере одно число, кратное 8 или 12.

Отсюда число подмножеств второго типа (которое как раз нам нужно найти) равно

Ответ:

Задача 2. Найти число разложений заданного числа в сумму слагаемых. Разложения, отличающиеся перестановкой слагаемых, считаются различными.

Варианты

1. Слагаемые состоят из чисел 3 и 4, сумма равна 50.

2. Слагаемые состоят из чисел 3 и 5, сумма равна 50.

3. Слагаемые состоят из чисел 2 и 5, сумма равна 50.

4. Слагаемые состоят из чисел 3 и 4, сумма равна 52.

5. Слагаемые состоят из чисел 3 и 5, сумма равна 52.

6. Слагаемые состоят из чисел 2 и 5, сумма равна 52.

7. Слагаемые состоят из чисел 3 и 4, сумма равна 54.

8. Слагаемые состоят из чисел 3 и 5, сумма равна 54.

9. Слагаемые состоят из чисел 2 и 5, сумма равна 54.

10. Слагаемые состоят из чисел 3 и 4, сумма равна 51.

11. Слагаемые состоят из чисел 3 и 5, сумма равна 51.

12. Слагаемые состоят из чисел 2 и 5, сумма равна 51.

13. Слагаемые состоят из чисел 3 и 4, сумма равна 49.

14. Слагаемые состоят из чисел 3 и 5, сумма равна 49.

15. Слагаемые состоят из чисел 2 и 5, сумма равна 49.

16. Слагаемые состоят из чисел 3 и 4, сумма равна 55.

17. Слагаемые состоят из чисел 3 и 5, сумма равна 55.

18. Слагаемые состоят из чисел 2 и 5, сумма равна 55.

19. Слагаемые состоят из чисел 3 и 4, сумма равна 46.

20. Слагаемые состоят из чисел 3 и 5, сумма равна 46.

21. Слагаемые состоят из чисел 2 и 5, сумма равна 46.

22. Слагаемые состоят из чисел 3 и 4, сумма равна 48.

23. Слагаемые состоят из чисел 3 и 5, сумма равна 48.

24. Слагаемые состоят из чисел 2 и 5, сумма равна 48.

25. Слагаемые состоят из чисел 3 и 4, сумма равна 53.

26. Слагаемые состоят из чисел 3 и 5, сумма равна 53.

27. Слагаемые состоят из чисел 2 и 5, сумма равна 53.

28. Слагаемые состоят из чисел 3 и 4, сумма равна 47.

29. Слагаемые состоят из чисел 3 и 5, сумма равна 47.

30. Слагаемые состоят из чисел 2 и 5, сумма равна 47.

31. Слагаемые состоят из чисел 3 и 4, сумма равна 55.

32. Слагаемые состоят из чисел 3 и 5, сумма равна 45.

33. Слагаемые состоят из чисел 2 и 5, сумма равна 42.

34. Слагаемые состоят из чисел 3 и 4, сумма равна 42.

35. Слагаемые состоят из чисел 3 и 5, сумма равна 41.

36. Слагаемые состоят из чисел 2 и 5, сумма равна 41.

Примеры решения задачи 2.

Пример 1.

Найти число разложений заданного числа в сумму слагаемых. Разложения, отличающиеся перестановкой слагаемых, считаются различными. Слагаемые состоят из чисел 3 и 5, сумма равна 40.

Решение.

Найдем сначала число слагаемых, равных 3, и число слагаемых, равных 5, дающих в сумме число 40. С этой целью решим уравнение в целых числах

3x + 5y = 40, x0, y0.

Первое решение x=0, y=8. Чтобы найти другие решения, будем прибавлять по 5 к числу x и вычитать по 3 из числа y. Получим решения

x = 0, y=8;

x = 5, y=5;

x = 10, y=2;

Число последовательностей чисел, состоящих из x троек и y пятерок, равно . Отсюда находим числа разложений

при x = 0, y=8 -

при x = 5, y=5 -

при x = 10, y=2 -

Сумма этих чисел будет искомым числом разложений.

Ответ:

Задача 3. Перечисление функций. Для заданных m и n вычислить числа:

• функций {1,2, …, m}  { 1, 2, …, n}

• инъекций {1,2, …, m}  { 1, 2, …, n}

• сюръекций {1,2, …, n}  { 1, 2, …, m}

• неубывающих функций {0,1,2, …, m}  {0, 1, 2, …, n}

• возрастающих функций {0,1,2, …, m}  {0, 1, 2, …, n}

• неубывающих сюръекций {0,1,2, …, n}  {0, 1, 2, …,m}

Варианты

1. m = 4 , n = 5	9. m = 6 , n = 8	17. m = 3 , n = 7	25. m = 2 , n = 10	33. m = 7 , n = 9
2. m = 5 , n = 6	10. m = 5 , n = 8	18. m = 2 , n = 7	26. m = 3 , n = 10	34. m = 8 , n = 9
3. m = 4 , n = 11	11. m = 4 , n = 8	19. m = 2 , n = 11	27. m = 4 , n = 10	35. m = 6 , n = 9
4. m = 5 , n = 9	12. m = 3 , n = 8	20. m = 4 , n = 6	28. m = 5 , n = 10	36. m = 5 , n = 11
5. m = 4 , n = 9	13. m = 2 , n = 8	21. m = 3, n = 6	29. m = 6 , n = 10
6. m = 3 , n = 9	14. m = 6 , n = 7	22. m = 2 , n = 6	30. m = 7 , n = 10
7. m = 2 , n = 9	15. m = 5 , n = 7	23. m = 3 , n = 5	31. m = 8 , n = 10
8. m = 7 , n = 8	16. m = 4 , n = 7	24. m = 3 , n = 11	32. m = 9 , n = 10

Пример решения задачи 3. Заданы m=6, n=11.

Вычислить числа:

• функций {1,2, …, 6}  { 1, 2, …, 11}

• инъекций {1,2, …, 6}  { 1, 2, …, 11}

• сюръекций {1,2, …, 11}  { 1, 2, …,6}

• неубывающих функций {0,1,2, …, 6}  {0, 1, 2, …, 11}

• возрастающих функций {0,1,2, …, 6}  {0, 1, 2, …, 11}

• неубывающих сюръекций {0,1,2, …, 11}  {0, 1, 2, …,6}

Решение.

Обозначим L_n = {1,2,3, …, n}. Искомые числа вычисляются с помощью таблицы, в каждой клетке которой указано число функций L_mL_n с заданными свойствами

	функций LmLn	Неубывающих функций LmLn
Всех	nm
Инъективных
Сюръективных	n! S(m,n)
Биективных	n!, если m=n, иначе 0	1, если m=n, иначе 0

Возрастающие функции – это в точности неубывающие инъективные функции. Находим

• число функций {1,2,3,4,5,6 }  { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,11} равно 11⁶=1771561

• число инъекций {1,2,3,4,5,6 }  { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,11 } равно = 332640

• число сюръекций { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,11 }  {1,2,3,4,5,6 } равно 6! S(11,6). Число S(11,6) вычислим с помощью таблицы

n k	1	2	3	4	5	6	7	8	9
1	1
2	1	1
3	1	3	1
4	1	7	6	1
5	1	15	25	10	1
6	1	31	90	65	15	1
7	1	63	301	350	140	21	1
8	1	127	966	1701	1050	266	28	1
9	1	255	3025	7770	6951	2646	462	36	1
10	1	511	9330	34105	42525	22827	5880	750	45
11						179487

Получим 6!S(11,6) =6!179487

• число неубывающих функций {0,1,2,3,4,5,6 }  { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,11 } равно

• число возрастающих функций {0,1,2,3,4,5,6 }  { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,11 } равно

• число неубывающих сюръекций { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,11 }  {0,1,2,3,4,5,6 } равно

Задача 4. Найти производящую функцию последовательности

Варианты

2nn(n+1) 2n/n 2nn2 2n/(n(n+1)) 3nsin(2n) 3ncos(2n) 4nn(n+1) 4n/n 4nn2 4n/(n(n+1)) 6n/n 3nsin(4n)

3ncos(4n) 7nn(n+1) 7n/n 7nn2 7n/(n(n+1)) sin(7n) cos(7n) 5nn(n+1) 5n/n 6nn2 5nn2 5n/(n(n+1))

5nsin(5n) 5ncos(5n) 3nn(n+1) 3n/n 3nn2 3n/(n(n+1)) sin(3n) cos(3n) 7nn(n+1) 7n/n 7nn2 3n/(n(n+1))

Пример решения задачи 4.

Найти производящую функцию последовательности a_n = 10ⁿ/(n(n+1))

Решение.

Производящая функция будет равна сумме ряда .

Поскольку , то

С помощью преобразования

получаем

Вычислим =

Следовательно

Ответ:

Задача 5. Коды Прюфера

Построить дерево по его коду Прюфера и сделать проверку

Варианты

15371 76412 26415 76421 16415 65413 36412 46715 16415 77411 74422 17251

15311 76422 26425 76431 16425 65423 36421 46725 16425 77421 74431 31625

11371 73412 22415 71421 13415 62413 31412 43715 12415 71411 72422 72112

Пример решения задачи 5

Построить дерево по его коду Прюфера 71543 и сделать проверку

Решение.

Выполним распаковку кода Прюфера. С этой целью в верхней строке выпишем заданный код. Под этим кодом выпишем последовательность состоящую из чисел 1, 2, …, m+2, где m – длина кода:

1, 2, 3, 4, 5, 6, 7

7, 1, 5, 4, 3

Положим B={1, 2, 3, 4, 5, 6, 7}. Через a_i обозначим i-й элемент кода. В частности a₁=7, a₂=1, a₃=5 и т.д. Будем выполнять цикл, на каждой итерации которого находится ребро дерево и удаляется элемент из множества B. На i-й итерации цикла, при i = 1, 2, …, m+1, минимальный элемент bB, среди не равных никакому из a_j  j ≥ i, соединяется с a_i и затем удаляется из B. Цикл выполняется для i=1, 2, 3, 4, 5. В нашей задаче

При i=1 наименьший из {1, 2, 3, 4, 5, 6, 7} среди не равных {7,1,5,4,3}

равен b=2. Присоединяем ребро {7,2}. Вычеркиваем 2 из верхней последовательности, и 7 – из нижней. B = B\{2} ={1, 3, 4, 5, 6, 7}.

При i=2 наименьший из {1, 3, 4, 5, 6, 7} среди не равных {1,5,4,3}

равен b=6. Присоединяем ребро {1,6}. Вычеркиваем 6 из верхней последовательности, и 1 – из нижней. B = B\{6} ={1, 3, 4, 5, 7}.

При i=3 наименьший из {1, 3, 4, 5, 7} среди не равных {5,4,3}

равен b=1. Присоединяем ребро {5,1}. Вычеркиваем 1 из верхней последовательности, и 5 – из нижней.B = B\{1} ={3, 4, 5, 7}.

При i=4 наименьший из {3, 4, 5, 7} среди не равных {4,3}

равен b=5. Присоединяем ребро {4,5}. Вычеркиваем 5 из верхней последовательности, и 4 – из нижней.B = B\{5} ={3, 4, 7}.

При i=5 наименьший из {3, 4, 7} среди не равных {3}

равен b=4. Присоединяем ребро {3,4}. Вычеркиваем 4 из верхней последовательности, и 3 – из нижней. B = B\{4} ={3, 7}.

Цикл закончился. Соединяем два оставшихся элемента 3 и 7.

Полученное дерево состоит из ребер {7,2}, {1,6}, {5,1}, {4,5}, {3,4}, {3,7}.

Рис. 2. Дерево с кодом 71543

Сделаем проверку. С этой целью построим код для полученного дерева. Построение кода состоит из цикла, на каждой итерации которого удаляется висячая вершина с наименьшим номером и выписывается номер вершины, соединенной с висячей.

В данном случае удаляем 2 и выписываем 7. Затем удаляем 6 и выписываем 1. Затем удаляем 1 и выписываем 5. Удаляем 5 и выписываем 4. Удаляем 4 и выписываем 3. Цикл заканчивается, когда останется две вершины. В результате получаем код, состоящий из выписанных чисел 7, 1, 5, 4, 3. Этот код совпадает с заданным. Следовательно, дерево построено верно.

Ответ: Дерево состоит из ребер {7,2}, {1,6}, {5,1}, {4,5}, {3,4}, {3,7}.

Задача 6. Моноиды

Задано вещественное число  и подмножество M  R множества вещественных чисел. Будет ли M относительно операции x*y = x + y + xy моноидом? Группой? Ниже N = {0,1,2, ...} обозначает множество натуральных чисел, Q – множество рациональных дробей m/n (где m,n  Z, n0).

Варианты

1. M = [0, 1[ ,  = –1	19. M = Q ,  = ½
2. M = [0, 1[ ,  = –2	20. M = [0, ½] ,  = –2
3. M = ]-1, 1[ ,  = –1	21. M = [0, 5] ,  = –1/5
4. M = {0, 1} ,  = –1	22. M = N ,  = 2
5. M = N,  = –1	23. M = R ,  = – ½
6. M = R ,  = 1	24. M = Q ,  = – 1/3
7. M = [0, 1] ,  = –2	25. M = N ,  = 0
8. M = Q ,  = 2	26. M = ] –1,0] ,  = 1
9. M = R \ {1} ,  = –1	27. M = ] –1,0] ,  = 2
10. M = R ,  = 2	28. M = ] –1,0] ,  = 3/2
11. M = R ,  = ½	29. M = [0,1] ,  = – 3/2
12. M = R ,  = – ½	30. M = Q ,  = ¾
13. M = N ,  = –2	31. M = ] –1,0] ,  = 4/3
14. M = [0, 1[ ,  = – 1	32. M = R \ {1/2} ,  = –2
15. M = Q ,  = 0	33. M = [0, 1/3] ,  = –3
16. M = R ,  = – 1	34. M = [0,1] ,  = – 4/3
17. M = [0, 1] ,  = – 3/2	35. M = Q ,  = 5/6
18. M = Q ,  = – 1	36. M = R \ {5/6}, a = - 6/5

Пример решения задачи 6.

Будет ли множество M = [0,1] с операцией x*y = x+y – (9/8)xy полугруппой? Моноидом? Группой?

Решение.

1) Проверим, будет ли x*yM при x,y M. Это выполнено если для всех удовлетворяющих неравенствам 0x, y1 чисел x, y будет иметь место 0x*y1. Рассмотрим произвольный 0y1. Функция f(x)= x+y – (9/8)xy при фиксированном y будет линейной по x. На концах интервала [0,1] она принимает значения f(0)=y и f(1)=1-(1/8)y. Поскольку эти значения лежат в интервале [0,1], то значения этой функции во внутренних точках интервала принадлежат [0,1]. Отсюда для всех x,y  M значения x*y принадлежат M.

2) Проверим ассоциативность (x*y)*z=x*(y*z). С этой целью раскроем обе части проверяемого равенства:

(x+y-(9/8)xy)+z-(9/8) (x+y-(9/8)xy)z = x+(y+z-(9/8)yz)-(9/8)x(y+z-(9/8)yz)

Поскольку последнее равенство имеет место, то операция * ассоциативна. Стало быть, (M,*) – полугруппа.

3) Проверим, будет ли (M,*) моноидом. Напомним, что моноидом называется полугруппа M, в которой существует элемент eM, удовлетворяющий для всех xM соотношениям x*e = e*x = x.

Этот элемент eM называется нейтральным. Для нахождения нейтрального элемента получаем тождество x+e –(9/8)xe = x , которое должно быть выполнено для всех xM. Легко видеть, что e=0 удовлетворяет этому тождеству. Отсюда вытекает, что (M,*) – моноид.

4) Проверим, будет ли (M,*) группой. Напомним, что моноид (M,*) называется группой, если для каждого x  M найдется такой y  M , что x*y = e. Отсюда данный моноид будет группой, если и только если для каждого x M существует yM, удовлетворяющий уравнению x+y-(9/8)xy = 0. Находим y = -x/(1-(9/8)x). Отсюда для x=8/9 это уравнение не имеет решений. Стало быть, заданный моноид не является группой.

Ответ: (M,*) является полугруппой, моноидом, но не является группой