§1.1. Способы задания множеств

Множество можно задавать перечислением его элементов, или как под-множество элементов, обладающих некоторым свойством, или как образ некоторого множества относительно отображения:

1. M = { a₁ , a₂ , ∙∙∙ , a_k  }, нет равных элементов a_i и a_j ,при i ≠ j.

2. M = { x A: P(x) }, где P(x) – некоторое свойство, выполнение которого зависит от элемента x множества A.

3. M = {f( x): x A }, где A – множество.

Свойство P(x) может быть получено из простейших формул с помощью логических операций: & (и),  (или), ~ (не),  (следует) и кванторов (для всех),  (существует). Например, свойство P(x) , выраженное формулой

(x  Z) & (x>0) & (y)((y  Z)& (x=y+y)),

имеет место, если и только если x – положительное целое число, кратное 2.

§1.2. Операции

Все множества предполагаются содержащимися в некотором множестве, “универсуме” U. Ниже через {x: P(x)} будет обозначать множество элементов xU, удовлетворяющих условию P(x).

• Пересечение множеств A и B определяется как AB={x: xA &xB},

• объединение множеств AB={x: xA  xB},

• разность множеств A\B={x: xA & ~(xB)} ,

• симметрическая разность AB= A\BB\A,

• дополнение =U\A,

• объединение семейства множеств A_i = {x:(iI) xA_i },

• пересечение семейства множеств A_i = {x:(iI) xA_i } ,

• количество элементов конечного множества |A|.

§1.3. Перечисление подмножеств

Пусть 2^M = { A : A  M } – множество всех подмножеств множества M.

Теорема 1. М – конечное  | 2^M | = 2^{| M |}

Доказательство. Пусть M = {a₀, a₁, , a_n-1 } – множество. Каждому подмножеству соответствует битовая строка, состоящая из 0 и 1. Бит[i] = 1, если a_i A, и Бит[i]=0, в других случаях. Хорошо известно, что количество двоичных n-разрядных чисел равно 2ⁿ .

Упражнение 1. Докажите теорему 1 с помощью индукции по числу элементов множества M.

Замечание 1.

1. Получаем алгоритм перебора подмножеств. Каждому подмножеству соответствует целое число, битовая строка которого соответствует этому подмножеству. Прибавляя по 1, получаем все подмножества.

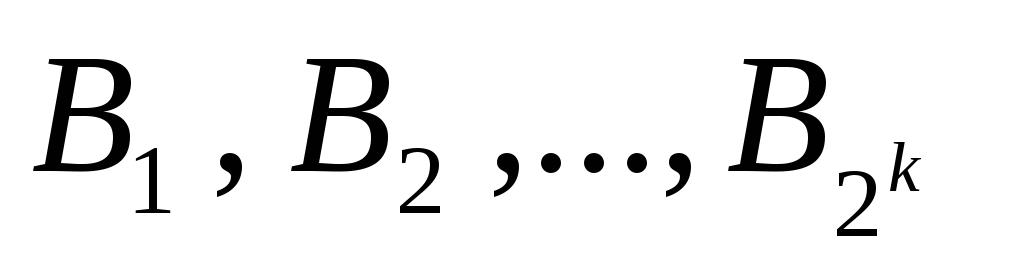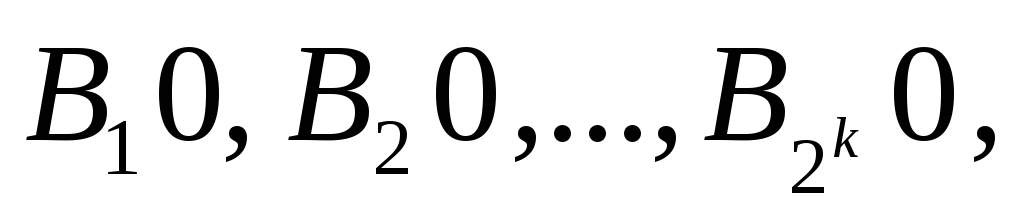
2. (Код Грея) Пусть получены двоичные коды подмножеств множества, состоящего из k элементов. Тогда – коды подмножеств множества, состоящего из k+1 элементов.

§1.4. Отношения и функции

Перечисление элементов декартового произведения. Декартовым произведением множеств называется множество, состоящее из упорядоченных пар: AB={(a,b): (aA) & (bB)}. Декартово произведение семейства множеств {A_i }_iI определяется как множество, состоящее из таких функций f: I  A_i , что для всех iI верно f(i)  A_i .

Теорема 1. A и B – конечные | AB| = | A||B| .

Следствие 1. |Aⁿ|=|A|ⁿ.

Доказательство. C помощью индукции по n.

Отношения и графы.

Определение 1. Ориентированным графом называется пара множеств (E,V) вместе с парой отображений s, t: EV. Элементы множества V изображаются точками на плоскости и называются вершинами. Элементы из E называются направленными ребрами или стрелками. Каждый элемент eE изображается в виде стрелки (возможно, криволинейной), соединяющей вершину s(e) с вершиной t(e).

Произвольному бинарному отношению RVV соответствует ориентированный граф с вершинами vV, стрелками которого являются упорядоченные пары (u,v) R.

Пример 1. Пусть V={1,2,3,4}. Рассмотрим отношение R={(1,1), (1,3), (1.4), (2,2), (2,3), (2,4), (3,3), (4,4) }. Ему будет соответствовать ориентированный граф (рис. 1.1). Стрелками этого граф будут пары (i,j) R.

Рис. 1.1. Ориентированный граф бинарного отношения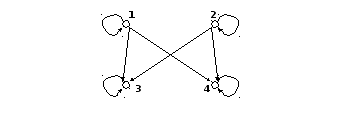

Определение 2. Простым (неориентированным) графом =(V,E) называется пара, состоящая из множества V и бинарного антирефлексивного симметричного отношения EVV. Элементы из V называются вершинами, а из E – ребрами.

Простой граф можно определить как множество V вершин вместе с множеством двухэлементных подмножеств EP(V). Вершины простого графа изображаются как точки, а ребра – как отрезки. На рис. 1.2 изображен простой граф с множеством вершин V={1, 2, 3, 4} и множеством ребер E = {{1,2}, {1,3},{1,4}, {2,3}, {2,4}, {3, 4}}.

Рис. 1.2. Простой неориентированный граф K₄