Теорема 1. Числа Каталана равны .

Доказательство. Имеют место соотношения для чисел классов бинарных деревьев:

c_k = c₀c_k-1 + c₁c_k-2 + ∙ ∙ ∙ +c_k-1c₀ , для всех k>0.

Пусть C(x) =  производящая функция последовательности чисел Каталана.

Получаем C(x) = xC²(x)+1, откуда .

§4.6. Плоские графы

Эйлерова характеристика. Односвязной двумерной клеткой мы будем называть часть поверхности, гомеоморфную единичному кругу D={(x,y): x²+y²  1}.

Теорема 1. Пусть   граф, разбивающий замкнутую поверхность S на односвязные двумерные клетки. Пусть p  число вершин графа, q – число ребер, r – число клеток. Тогда число p – q + r не зависит от разбивающего графа и называется эйлеровой характеристикой поверхности.

Теорема 2. Пусть   связный граф, разбивающий сферу на односвяз-ные клетки. Тогда p – q + r = 2.

Доказательство. С помощью индукции по q. Если q=0, то p=1 и r=1. Пусть теорема верна для графа с q ребрами. Докажем ее для q+1 ребер. Рассмотрим два случая добавления ребра:

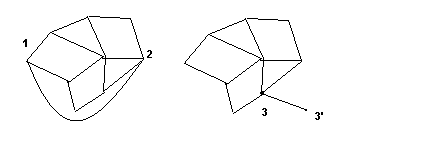
В первом случае добавляется ребро, вершины не добавляются. Во втором добавляется ребро и вершина. Если обозначить новые числа вершин, ребер и граней через p’, q’, r’, то в первом случае получим p’–q’+r’ = p – (q+1)+(r+1) = p–q+r =2, во втором ─ p’–q’+r’ = (p+1) – (q+1)+r = p–q+r =2.

Графы Куратовского. Далее мы рассмотрим следующие две задачи.

Первая задача принадлежит Мебиусу. Речь идет о короле, завещавшем своим пяти сыновьям разделить между собой его владения так, чтобы каждая из частей имела общие границы с каждой из остальных частей.

Рассматривая граф, вершины которого соответствуют пяти частям, а ребра – общим границам, приходим к вопросу, является ли он плоским?

Вторая задача – задача о трех домах и трех колодцах. На поверхности сферы заданы 3 точки, называющиеся домами, и 3 точки, называющиеся колодцами. Нужно соединить не пересекающимися кривыми (играющими роль тропинок) каждый дом со всеми колодцами.

Докажем неразрешимость этих двух задач.

Лемма 1. Для связного плоского графа с p>3 вершинами и q ребрами справедливо неравенство q  3p-6. Если существует вложение в сферу, при котром каждая грань имеет ≥ 4 ребер, то справедливо неравенство q  2p – 4.

Доказательство. Рассмотрим множество пар (ребро, грань), где ребро содержится в грани. Число таких пар равно 2q , ибо каждое ребро принадлежит двум граням. С другой стороны, оно не меньше 3r , ибо грань содержит не меньше трех ребер. Отсюда 2q ≥ 3r. Если грань содержит не меньше четырех ребер, то получаем 2q ≥ 4r . Подставляя в эти неравенства r = 2 – p +q, получим доказываемые неравенства.

Следствие 1. Граф k5 не плоский.

Доказательство. Граф K₅ имеет 5 вершин и 10 ребер. Неравенство 10  3∙5 – 6 неверно, значит он не плоский.

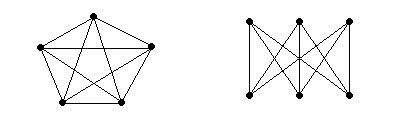
K₅ K_3,3

Следствие 2. Граф k3,3 не плоский.

Доказательство. В графе K_3,3 нет циклов длины 3. Отсюда в случае существования вложения в сферу каждая грань будет иметь  4 ребер. По лемме, в этом случае имеет место неравенство q 2p –4. Так как неравенство 9  2∙6 – 4 неверно, то граф K_3,3 не плоский.

Следовательно, обе задачи неразрешимы.

Следующая теорема Куратовского характеризует плоские графы.

Теорема 3. Граф плоский тогда и только тогда, когда он не содержит ни графа гомеоморфного K₅ , ни графа гомемоморфного K_{3, 3} .

Раскраска плоского графа. Следующий вопрос – о раскраске плоских графов. В 1878 году эта проблема была поставлена Кэли на заседании Лондонского математического общества. Задана карта, состоящая из областей на сфере, которые можно интерпретировать как страны, расположенные на земной поверхности. Можно ли произвольную такую карту раскрасить в четыре цвета так, чтобы любые две имеющие общую границу страны были окрашены в различный цвет?

Положительное решение этой проблемы было опубликовано в 1977 году Аппелем и Хакеном.

Мы докажем, что пять цветов достаточно для раскраски любой карты. Метод доказактельства был предложен А.В. Кэмпе, и долгое время считалось, что этот метод годится и для четырех красок. Но это мнение было опровергнуто в 1890 году Хивудом.

Задача сводится к правильной раскраске вершин плоского графа, вершины которого соответствуют странам, а соединение вершин ребром осуществляется при наличии общей границы у стран.