Теорема 1. Граф является эйлеровым тогда и только тогда, когда нечетную степень имеют не более двух вершин.
Доказательство. Сначала доказывается, что существование содержащего все ребра замкнутого пути без кратных ребер равносильно четности всех вершин. Если граф эйлеров, то добавим ребро, соединяющее первую и последнюю вершину эйлерового пути. Получим, что все вершины дополненного графа имеют четные степени.
Пример 1. Закрытое письмо (см. Рис. 4.2) невозможно нарисовать не отрывая карандаш и проходя каждую линию ровно один раз, а открытое – можно.
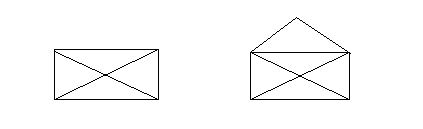
Рис. 4.2. Закрытое письмо и открытое письмо
Отметим две другие задачи: Задача о трех домах и трех колодцах и задача о наследстве. В последней из них требуется разделить плоскую односвязную область на пять односвязных областей, каждая пара которых имеет общую границу ненулевой длины.
Хорошо известна задача о раскраске плоской карты в четыре цвета. Она была решена Аппелем, Рингелем и Янгсом в 1971 году с помощью ЭВМ.
§4.2. Простые графы и их свойства
Ниже повсюду мы будем рассматривать графы, у которых между любыми двумя вершинами существует не более одного инцидентных им ребра. Ребра можно рассматривать как пары ={u,v}. Напомним, что такие графы называются простыми. Иногда мы будем называть их просто графами.
Теорема
1.
(Теорема
Эйлера о сумме степеней вершин графа)
Пусть d(v)
обозначает степень вершины v.
Для произвольного простого графа
=(V,E)
верно соотношение
.
Доказательство. Рассмотрим упорядоченные пары (v,), состоящие из вершины v инцидентой ребру . Количество таких пар равно сумме степеней вершин. С другой стороны, оно равно удвоенному числу ребер.
Замечание. Теорема Эйлера имеет место и для графов, не являющихся простыми. §4.3. Хроматическое число графа
Определение 1. Раскраска вершин графа =(V,E) называется правильной, если любые две смежные вершины окрашены в различные цвета. Минимальное число цветов, необходимое для правильной раскраски, называется хроматическим числом графа и обозначается ().
Теорема 1. Следующие свойства графа равносильны
() 2 ;
двудольный ;
каждый элементарный цикл в графе имеет четную длину.
Доказательство. Равносильность (1) и (2) очевидна. Импликация (3) (2) получается разбиением вершин, на вершины имеющие путь четной длины из фиксированной вершины, и имеющие путь нечетной длины. Импликация (2) (3) очевидна.
Определение 2. Хроматической функцией f(q) графа =(V,E) называется число правильных раскрасок с помощью q красок.
Пример 1.Для дискретного графа с n вершинами f(q)=qn.
Вершина vV графа =(V,E) называется висячей, если ее степень d(v) равна 1.
Теорема 2.Для дерева T имеющего число вершин n хроматическая функция равна f(q)=q(q – 1)n-1.
Доказательство по индукции. Удалим висячую вершину (которая существует в силу формулы Эйлера и соотношения |E|+1=|V|). Получим дерево, которое можно раскрасить q(q-1)n-2 способами, согласно предположению индукции. Затем снова присоединим удаленную вершину. Для каждой из q(q-1)n-2 раскрасок ее можно раскрасить (q-1) способами. Отсюда получаем доказываемую формулу.
Пример 2. Вычислим хроматическую функцию графа, состоящего из двух имеющих общую сторону треугольников
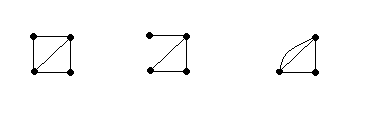
Рис. 4.3. Удаление ребра и склеивание двух вершин
С этой целью удалим ребро. Получим граф, показанный на рисунке 4.3 вторым. Он имеет q(q-1)(q-2)(q-1) правильных раскрасок. Но не все раскраски являются правильными для исходного графа. Число раскрасок, у которых концы удаленного ребра имеют одинаковый цвет, нужно вычесть. Число таких раскрасок равно значению хроматического многочлена графа, изображенного на рисунке третьим. Отсюда f(q)= q(q –1)(q–2)(q–1) –q(q–1)(q–2).
Рассмотренный в примере 2 метод годится для вычисления f(q) в общем случае: