
ТОИИТ / Задания
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
31 |
|
|
|
|
1 T |
|
|
|
|
|
− jnω t |
|
|
|
|
jφ |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
& |
|
|
|
T |
∫ |
|
|
|
|
|
|
|
|
o |
|
& |
|
|
|
n |
|
|
|
|
|
|
C |
n |
= |
|
|
|
S |
(t)e |
|
|
|
|
|
dt = |
C |
e |
|
|
. |
|
|
|
(2.4) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Между коэффициентами |
|
C& |
n |
|
и A |
, а также ϕ |
n |
и Φ |
n |
существу- |
||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||||
ет простая связь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C = A ; |
C |
n |
= |
|
C& |
n |
|
= A / 2 , ( n ≠ 0 ); |
|
|
|
(2.5) |
||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||
Φn = ϕn ( n > 0 ); Φn = −ϕn ( n < 0 ).
На рис. 2.1, б приведен пример спектральных диаграмм комплексного ряда Фурье.
An |
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cn |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
A2 |
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
C |
C |
|
|
|
|
|
|
||||
A0 |
|
|
|
A3 |
|
|
|
|
|
|
|
|
C−2 |
|
|
|
C2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
0 |
|
|
1 |
|
|
C |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
C−3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щ0 2щ0 3щ0 щ |
|
−3щ0 |
−щ |
0 |
0 |
щ0 |
|
3щ0 |
щ |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||||
ϕn |
|
|
ϕ1 |
|
|
|
|
|
|
|
|
|
|
|
ϕ−2 |
|
|
|
|
ϕn |
|
|
ϕ |
|
|
|
ϕ3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
0 |
|
|
|
|
ϕ3 |
|
|
|
|
|
|
−щ0 |
|
|
|
1 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щ |
||||||
|
|
щ |
0 ϕ2 |
|
3щ0 щ |
|
ϕ |
|
|
−2ω0 |
|
|
|
|
|
|
щ |
0 |
|
3ω0 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
−3 |
ϕ−1 |
|
|
|
|
|
|
ϕ2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.2.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Важно! Коэффициенты |
A |
|
и C& |
могут быть вычислены двумя |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
способами:
•непосредственно по (2.2) и (2.4);
•с использованием спектральной плотности (2.10).
Для периодических сигналов, а также для сигналов с ограниченной областью определения в качестве энергетической характеристики используется средняя мощность, которую можно вычислить по формулам:
•для временной области
1 T
P = ∫S 2 (t)dt ; (2.6)
T 0

32ГЛАВА 2. СПЕКТРАЛЬНЫЕ ФОРМЫ ПРЕДСТАВЛЕНИЯ СИГНАЛОВ
•для частотной области
|
|
|
|
|
|
|
∞ |
|
|
∞ |
|
|
|
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
= A02 + ∑An2 |
/ 2 = ∑ |
C&n |
|
|
|
|
|
|
|
|
|
|
|
|
(2.7) |
||||||||||||
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
n=1 |
|
|
n=−∞ |
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||
Совокупность коэффициентов |
A |
2 |
/ 2 и |
|
|
C |
= |
|
& |
|
|
образует дис- |
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
n |
|
C |
n |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
кретный спектр мощности периодического сигнала (рис. 2.2). |
|
|
||||||||||||||||||||||||||||||
An2 / 2 A2 |
/ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cn2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
A2 |
/ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A02 |
|
|
2 |
|
A32 / 2 |
C−23 |
|
|
|
C−21 |
|
|
C02 |
|
|
C12 |
|
C22 C2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щ0 2щ0 3щ0 щ |
−3щ |
|
|
|
−щ |
|
|
|
0 |
|
|
|
щ |
2щ 3щ |
|
щ |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
0 |
0 |
0 |
|
||||||
Рис.2.2
Важно! При переходе к спектру мощности теряется информация о фазе спектральных составляющих.
В отличие от периодического сигнала, одиночный импульс, заданный на всей бесконечной оси времени ( T0 → ∞ ), включающей
область определения сигнала ( Tопp ), не может быть записан как ряд
Фурье. Логическим распространением спектральных представлений на одиночные импульсы является интегральное преобразова-
ние.
Прямое преобразование Фурье – это переход от описания сигна-
ла во времени S(t) к описанию в частотной области S&(ω)
∞ |
|
S&(ω) = S( jω) = ∫ S(t)e− jωt dt = S&(ω) e jϕ(ω) . |
(2.8) |
−∞
Обратное преобразование Фурье – это восстановление времен-
ной модели сигнала по его спектральной плотности
|
1 |
∞ |
|
|
S(t) = |
∫ S&(ω)e jωt dω. |
(2.9) |
||
2π |
||||
|
−∞ |
|
||
|
|
|
Таким образом, одиночный импульс, заданный на всей бесконечной оси времени, имеет сплошной спектр в виде непрерывной
функции частоты S&(ω) , которая называется спектральной плотностью. Размерность спектральной плотности [Ампл / Гц].

33
На рис. 2.3 приведен пример спектральных диаграмм модуля (б) и фазы (в) спектральной плотности для одиночного прямоугольного импульса (а).
S(t) U |
S( f ) |
|
|
|
|
Uф |
|
|
|
−ф/ 2 0 ф/ 2 t |
−2 / ф |
0 1/ф 2/ф 3/τ |
f |
|
а |
|
б |
|
|
|
ϕ( f ) |
|
|
|
|
2р |
2/ф 3/ф |
|
|
−2 / ф |
р |
f |
|
|
−р |
|
|
|
|
|
−2р |
|
|
|
в
Рис.2.3
Спектральная плотность связана простым соотношением с ком-
∞
плексными амплитудами периодического сигнала ∑S (t + nT0 ) ,
n=0
полученного повторением с периодом T0 одиночного импульса S(t).
. |
1 . |
|
|
|
|
Cn = |
|
S(nω ) , ω |
0 |
= 2π/ T . |
(2.10) |
|
|||||
|
0 |
0 |
|
||
|
T0 |
|
|
|
|
Соотношение (2.10) позволяет легко перейти от сплошного спектра одиночного импульса к дискретному спектру периодиче-
ской последовательности импульсов. Расчет С&n по соотношению (2.10) рекомендуется проводить еще и потому, что
•спектральная плотность большинства простейших одиночных импульсов широко представлена [1-3];
•при расчете спектра сложных импульсных последовательностей можно воспользоваться основными теоремами о спектре
(прил. П.4).
Полная энергия одиночного импульса может быть вычислена либо во временной области, либо в частотной в соответствии с равенством Парсеваля:

34 ГЛАВА 2. СПЕКТРАЛЬНЫЕ ФОРМЫ ПРЕДСТАВЛЕНИЯ СИГНАЛОВ
Эс = |
∞ |
S 2 (t) |
dt = |
1 ∞ |
|
S&(ω) |
|
2 dω. |
|
||
|
|
|
(2.11) |
||||||||
|
|
|
|||||||||
∫ |
π ∫ |
||||||||||
|
|
|
|
|
|
|
|
||||
|
−∞ |
|
|
0 |
|
|
|
|
|
||
.
Спектральная диаграмма | S(ω) |2 , как функция частоты, называется
энергетическим спектром одиночного импульса.
Для оценки эффективной (практической или активной) длительности сигнала ( τэф ), имеющего бесконечно протяженную во
времени математическую модель, можно воспользоваться энергетическим критерием:
τэф |
|
Эс(τэф) = ∫ S 2 (t) dt = kэЭс . |
(2.12) |
0 |
|
В частотной области аналогичным способом определяют эффективную ширину спектра сигнала ( ωэф )
|
1 |
ωэф . |
|
||
Эс(ωэф) = |
∫ |
| S(ω) |2 dω = kэЭс . |
(2.13) |
||
π |
|||||
|
|
0 |
|
|
|
Таким образом, эффективная длительностьτэф (и ширина спектраωэф ) – это такой временной (и частотный) интервал, в котором сосредоточена подавляющая часть ( kэ ) полной энергии сигнала.
Обычно kэ = 0.9 (90%) или 0.95 (95 %).
Между эффективной длительностью и шириной спектра простейших видеоимпульсов имеется связь, которая называется соот-
ношением неопределенности для сигналов
τэф fэф = μ , |
(2.14) |
где fэф = ωэф / 2π; μ – небольшое число (см. прил. П.5).
Одной из важных временных характеристик детерминированных сигналов, устанавливающих энергетическую связь сигнала S(t) с его сдвинутой на величину τ копией S(t − τ) , является ав-
токорреляционная функция (АКФ). Для сигналов с ограниченной областью определения АКФ вычисляется по формуле
∞ |
|
Ks (τ) = ∫ S(t)S(t − τ)dt . |
(2.15) |
−∞

35
Для периодических сигналов ST (t + nT0 ) АКФ вычисляется:
|
1 |
T / 2 |
|
|
ks (τ) = |
0∫ ST (t)ST (t − τ)dt . |
(2.16) |
||
T |
||||
|
0 −T / 2 |
|
||
0 |
|
|||
В теории сигналов доказывается, что АКФ и энергетический спектр связаны парой преобразований Фурье
|
|
|
. |
|
|
|
|
Ks (τ) | S(ω) |2 . |
(2.17) |
Основные свойства АКФ: |
|
|||
1) Ks (τ) = Ks (−τ) |
– четность; |
|
||
2) Ks (0) = Эс |
– полная энергия сигнала; |
|
||
ks (0) = |
|
|
– средняя за период мощность сигнала; |
|
P |
||||
3) Ks (0) ≥ Ks (τ) |
– максимум в начале координат; |
4) ks (τ) = ks (τ + nT0 ) |
– АКФ периодического сигнала –периоди- |
|
ческая функция с периодом T0 ; |
5) Ks (τ) и ks (τ) |
– не несут информации о начальном поло- |
|
жении сигнала. |
Энергетическую связь двух различных сигналов, сдвинутых друг относительно друга на величину τ, характеризует взаимная корреляционная функция (ВКФ):
∞ |
|
Ks,u (τ) = ∫ S(t)U (t − τ)dt . |
(2.18) |
−∞
ВКФ отображается в частотную область как взаимный энергетический спектр:
& |
& |
& |
. |
|
|
(ω)U (ω) , |
(2.19) |
||||
Ks,u (τ) S |
(ω)U |
(ω) = S |
где “*” – знак комплексного сопряжения.
ВКФ связана с интегралом свертки следующим соотношением:
∞ |
|
Ks,u (τ) = S(τ) U (−τ) = ∫ S(ξ)U (ξ + τ)dξ . |
(2.20) |
−∞
Дискретные сигналы могут быть получены из аналоговых (непрерывных) дискретизацией. Простейшая математическая модель
36 |
ГЛАВА 2. СПЕКТРАЛЬНЫЕ ФОРМЫ ПРЕДСТАВЛЕНИЯ СИГНАЛОВ |
дискретного |
сигнала Sд(t) – это счетное множество точек {ti } |
(i = 0,1,2,...,) |
на оси времени, в каждой из которых известно значе- |
ние Si сигнала S(t) .
На основании теоремы Котельникова непрерывный сигнал S(t) , спектр которого не содержит частот выше fmax , полностью опре-
деляется дискретной последовательностью своих мгновенных значений, отсчитываемых через интервалы времени T :
T = |
1 |
= |
π |
, |
(2.21) |
||
2 f |
max |
ω |
|||||
|
|
|
|
||||
|
|
|
max |
|
|
||
где T – интервал дискретизации (интервал Найквиста).
Такой ограниченный по частоте сигнал можно выразить обобщенным рядом Фурье в базисе функций (sin x) / x :
|
|
∞ |
|
|
|
||
|
|
S(t) = ∑ S(kT )ϕk (t) , |
(2.22) |
||||
|
|
k =−∞ |
|
|
|
||
где |
ϕk (t) = |
sin[ωmax (t − kT )] |
– при |
k = 0, 1, 2, … система ортого- |
|||
ωmax (t − kT ) |
|
||||||
|
|
S(kT ) |
– значения функции S(t) |
|
|||
нальных базисных функций; |
в мо- |
||||||
менты времени kT . |
|
|
|
||||
|
Для представления сигналов конечной длительности ( Tопр ) в |
||||||
дискретной форме потребуется N отсчетов |
|
||||||
|
|
N = Tопр / T = 2 fmaxToпp , |
(2.23) |
||||
где N – база сигнала. Обратим внимание, что при этом частота fmax определяется приближенно, так как сигналы, ограниченные
во времени, имеют бесконечно протяженный спектр.
Спектр дискретизированного сигнала отличается от спектра непрерывного сигнала тем, что он периодичен по частоте. Если за дискретизирующую последовательность принята система дельтафункций
∞
ϕk (t) = ∑ δ(t − kT ) ,
k =−∞
то спектр дискретизированного сигнала имеет вид:
|
|
|
37 |
|
. |
1 |
∞ . |
|
|
S д(ω) = |
∑ S(ω− kωд) , |
(2.24) |
||
|
||||
|
T k =−∞ |
|
||
.
где S(ω) – спектр непрерывного сигнала; ωд = 2π/T = 2ωmax – частота дискретизации, являющаяся “периодом” повторения по частоте.
Для дискретизированного сигнала можно ввести дискретную функцию автокорреляции
∞ |
|
KS (n) = ∑ Sk Sk −n , |
(2.25) |
k =−∞
где Sk = S (kT ) , n =0, ±1, ±2, … .
2.3.ЗАДАЧИ
2.3.1.ГАРМОНИЧЕСКИЙ АНАЛИЗ ПЕРИОДИЧЕСКИХ СИГНАЛОВ
1.Вычислите спектр сигналов S1(t) ÷ S4 (t) , используя триго-
нометрическую форму ряда Фурье. Постройте графики сигналов во времени и соответствующие им спектральные диаграммы в частотной области
S1(t) =U0 +Um cos(ωнt + ϕ0 ) ;
S2 (t) =U0 +Um sin(ωнt + ϕ0 ) ;
S3 (t) =U0 +Um1 cos(ωнt) +Um2 sin(2ωнt) ;
S4 (t) =U0 +Um cos(ωнt) cos(2ωнt) .
2.Рассчитайте спектр сигналов S1(t) ÷ S4 (t) из задачи 1 и по-
стройте спектральные диаграммы, используя комплексную форму ряда Фурье.
3. Изобразите спектры мощности сигналов S1(t) ÷ S4 (t) из зада-
ния задачи 1. Определите среднюю за период мощность, используя временное и спектральное представление сигналов. Сравните результаты.
4. Как изменится спектр сигнала S1(t) из задачи 1, если сигнал
сдвинуть по оси времени на величину τ , - τ ? Как изменится его спектр мощности?

38 |
ГЛАВА 2. СПЕКТРАЛЬНЫЕ ФОРМЫ ПРЕДСТАВЛЕНИЯ СИГНАЛОВ |
5. Чем отличается спектр сигнала αS1(t) от спектра сигнала
S1(t) , если α =const?
6. Рассчитайте спектр и изобразите спектральную диаграмму сигнала
S (t) = αdS2 (t) / dt ,
где S2 (t) – сигнал из задачи 1.
7. Вычислите спектр и изобразите спектральные диаграммы сигнала
t
S(t)= ∫S1(t)dt , при U0=0, ϕ0=0,
0
где S1(t) – сигнал из задачи 1. 8. Изобразите спектр сигнала
S(t) = S1(βt) ; β = const.
9. Запишите аналитическое выражение математической модели сигнала (рис. 2.4). Определите период сигнала. Вычислите среднюю за период мощность.
An |
|
U |
|
|
|
|
|
|
ϕn |
|
|
р |
3р/2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||
U0 |
|
|
|
U / 2 |
U / 3 |
|
|
|
р/2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
щ |
2щ |
3щ |
щ |
0 |
щ 2щ |
3щ |
ω |
||||||||
|
|
0 |
0 |
0 |
|
|
0 |
0 |
0 |
|
|
|||||||
Рис.2.4
10. Математическая модель сигнала имеет вид
3 |
U |
m |
|
j(nω t+nπ/ 2) |
|
S(t) = ∑ |
|
e |
0 |
. |
|
|
|
||||
n=−3 |
2n |
|
|
||
Изобразите амплитудный спектр и спектр мощности сигнала. Поясните разницу.
11.Выведете выражение для расчета постоянной составляющей
иамплитуды n-й гармоники последовательности однополярных
импульсов S1(t) (рис. 2.5, а).
12. Какие гармоники будут отсутствовать в спектре сигнала S1(t) (рис. 2.5, а), если его скважность ( q =T / τ) равна 10?

39
13. Решите задачу 11 для частного случая, когда сигнал S1(t)
представляет собой периодическую последовательность знакопеременных прямоугольных импульсов S2 (t) (см. рис.2.5, б) с ам-
плитудой Um = S0 / 2 и со скважностью 2 (так называемый меандр).
14. По данным предыдущей задачи запишите ряд Фурье в тригонометрической форме и изобразите сумму первых трех составляющих (с частотами Ω, 2Ω и 3Ω ). Определите относительную
среднеквадратическую ошибку μ (см. (1.10)) такой аппроксима-
ции.
15. Как изменятся спектры амплитуд и фаз меандра (рис. 2.5, б), если S2 (t) переместить: а) по оси ординат вверх на Um ; по оси
абсцисс (времени) вправо на τ/ 2 ?
16. Для периодической последовательности импульсов S1(t)
(рис. 2.5, а), скважность которых равна 2, определите долю мощности, которая заключена в постоянной составляющей и первой гармонике (т. е. в первом “лепестке” огибающей спектра сигнала), от средней за период мощности сигнала. Какова доля мощности сигнала в двух “лепестках” его спектра?
S1 |
(t) |
|
|
S0 |
|
|
|
S2 (t) |
|
|
Um |
|
|
|
|||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
−ф/ 2 0 ф/ 2 |
T t |
|
|
|
|
|
|
|
|||||||||
−ф/ 2 |
|
ф/ 2 |
T |
|
|||||||||||||
|
|
|
|||||||||||||||
Рис.2.5
17. Найдите постоянную составляющую и амплитуду первой гармоники периодического сигнала S1(t) , изображенного на
рис.2.6, а.
S1(t) = Um cos ω0t , −τ/ 2 ≤ t ≤ τ/ 2 , τ =T / 2 = π/ ω0 .
18. Рассчитайте постоянную составляющую и амплитуду первой гармоники последовательности импульсов S2 (t) , представленной на
рис. 2.6, б и образованной гармоническим колебанием Um cos ωot , ограниченным на уровне Uo :
S2 (t) =Um cos ω0t −U0 , −τ/ 2 ≤ t ≤ τ/ 2 или −θ ≤ ω0t ≤ θ ,
где θ – так называемый угол отсечки, определяемый из соотношения
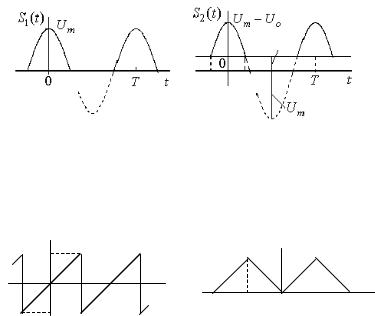
40 |
ГЛАВА 2. СПЕКТРАЛЬНЫЕ ФОРМЫ ПРЕДСТАВЛЕНИЯ СИГНАЛОВ |
Um cos θ =U0 ,
откуда θ = arccos(U0 /Um ) ; при этом ω0τ/ 2 = θ или τ = Найдите ao и A1 для частного случая, когда U0 = 0
сопоставьте с результатом задачи 17.
|
−и и р |
U0 |
|
2р |
|
−ф/ 2 ф/ 2 |
−ф/ 2 ф/ 2 |
|
а |
|
б |
|
Рис. 2.6 |
|
2θ/ ωo .
( θ = π/ 2 ) и
щ0t
19. Выведите выражение для расчета амплитуды n-й гармоники периодического колебания пилообразной формы S1(t) (рис. 2.7, а).
S1(t) |
|
|
S2 (t) |
|
|
|
|
Um |
|
|
S0 |
|
|
|
|
0 |
T |
t |
−T / 2 |
0 |
T / 2 |
T |
t |
−Um |
|
|
|||||
|
|
|
|
|
|
|
|
а |
|
|
|
|
б |
|
|
Рис.2.7
20. По данным предыдущей задачи запишите ряд Фурье в тригонометрической форме. Вычислите амплитуды первых трех гармоник и относительную среднеквадратическую ошибку μ аппрок-
симации для этого случая, т. е. когда S1(t) равно сумме трех со-
ставляющих.
21. Определите постоянную составляющую и амплитуду n-й гармоники последовательности униполярных треугольных импуль-
сов S2 (t) (рис. 2.7, б).
22. По результату решения предыдущей задачи определите относительную среднеквадратическую ошибку μ аппроксимации
S2 (t) суммой постоянной составляющей и трех первых гармоник.
