
ТОИИТ / Задания
.pdf
81
Z (t) = X (t)S(t) ,
где X (t) – эргодический случайный процесс с известными математическим ожиданием mx и дисперсией Dx и корреляционной функцией Kx (τ) , а S(t) – детерминированная функция. Можно ли процесс Z (t) назвать стационарным?
19. Определите математическое ожидание, дисперсию и корреляционную функцию процесса
Z (t) = X (t)S1(t) +Y (t)S2 (t) ,
где X (t) и Y (t) – некоррелированные стационарные случайные процессы с известными математическими ожиданиями mx и my , дисперсиями Dx и Dy и корреляционными функциями Kx (τ) и K y (τ) , а S1(t) и S2 (t) – детерминированные функции времени. Ста-
ционаренлипроцесс Z (t) ?
20. Задан случайный процесс
Z (t) = Asin(ω0t + ϕ) ,
где A и ω0 – положительные постоянные (амплитуда и частота), а ϕ – случайнаявеличина, равномернораспределённаянаотрезке[0, 2π], т. е. w(ϕ) =1/ 2π. Найдите математическое ожидание и дисперсию, а
также классифицируйте процесс попризнакам стационарности.
21. Докажите, что процесс Z (t) , рассмотренный в предыдущей задаче, эргодичен относительно математического ожидания и корреляционной функции. Найдите mz (t) и Kz (τ) усреднением по
времени.
22. Классифицируйте по признакам стационарности и эргодичности процесс
Z (t) = X (t) +Y ,
в котором X(t) – эргодический процесс с известными mx и Dx, а Y – случайная независимая от времени величина с заданными my и
Dy, изменяющаяся от одной реализации к другой.
23. Стационарный случайный процесс X(t) с заданными математическим ожиданием mx, дисперсией Dx и одномерной плотностью вероятности w(x) умножили на константу K, например, пропусти-
ли через широкополосную линейную цепь с коэффициентом передачи K .
82 |
ГЛАВА 4. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ |
Как изменятся указанные параметры случайного процесса?
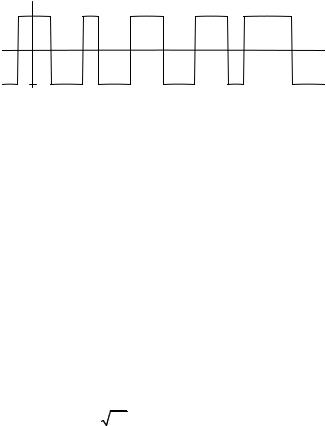
24.Найдите плотность вероятности, математическое ожидание
идисперсию процесса U (t) вида “телеграфного сигнала”, реализа-
ция которого u(t) показана на рис. 4.7.
Вероятность независимых перемен знаков, иначе “опрокидываний” подчиняется закону Пуассона
PT (n)= (λT )n exp(−λT ),
n!
где λ – среднее число “опрокидываний” в единицу времени, PT (n)
– вероятность того, что за период T произойдёт n “опрокидываний”; при этом P( A) = P(−A) = 0.5 .
u (t )
A
0 |
t |
− A
Рис. 4.7
25. Стационарный случайный процесс U (t) имеет функцию распределения F (u) =1 − exp(au) , u > 0, a > 0 .
Определите математическое ожидание, средний квадрат и дисперсию этого процесса.
26.По данным задачи 10 рассчитайте математическое ожидание, средний квадрат и дисперсию прямоугольного, треугольного и пилообразного колебаний со случайной задержкой.
27.Определите математическое ожидание и дисперсию стационарного случайного процесса, имеющего распределение по закону:
а) w(u) = (2 / π)cos2 (au), −π/ 2 < u < π/ 2;
б) w(u) = (1/ 4)ch(bu), −1 < u <1.
Коэффициенты a и b также подлежат определению.
28. Плотность вероятности усечённого нормального процесса U (t) имеет вид
w(u) = 0,5δ(u) + (1/ σu 2π) exp(−u2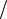 2σu2 ) при 0 < u < ∞.
2σu2 ) при 0 < u < ∞.

83
Изобразите примерный вид реализации этого процесса и найдите математическое ожидание, средний квадрат, дисперсию и среднеквадратическое значение случайного напряжения.
4.3.3.ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ. ЭНТРОПИЯ
29.Найдите характеристическую функцию случайной величины X, имеющей плотность вероятности:
а) w(x) =1/(b − a), a < x < b ;
б) |
w(x) = λexp(−λx), λ > 0, x > 0 . |
30. |
Покажите, что если закону w(x) соответствует характери- |
стическая функция θ(ν) , то закону w(x m x0 ) cоответствует характеристическая функция θ(v)exp(± jvx0 ).
31.Используя результаты, полученные в задаче 29, определите математическое ожидание mx случайной величины X .
32.Найдите характеристическую функцию нормального закона
w(x) = (1/ у 2р)exp[ − (x − a)2/2у2 ] .
33.Используя результат предыдущей задачи, найдите первые четыре момента нормального распределения.
34.Решите задачу 13 косвенным методом – на основе характеристических функций.
35.Найдите энтропию равномерного закона распределения вероятностей
w(x) =1/(b − a), a < x < b .
36. Определите энтропию нормального шума U (t) ; плотность вероятности определяется выражением
w(u) = (1/ у 2р)exp[ −(u − m)2/2у2 ] .
37.Используя результат, полученный в задачах 35 и 36, найдите разность энтропии нормального и равномерного законов при одном
итом же среднем квадратическом отклонении σ.
4.3.4.СПЕКТРАЛЬНЫЙ И КОРРЕЛЯЦИОННЫЙ АНАЛИЗЫ
38.Определите и изобразите графически СПМ Gx (ω) случайного процесса X (t) по его корреляционной функции Kx (τ) = Dexp(−a τ) .
84 |
ГЛАВА 4. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ |
Рассчитайте эффективную ширину спектра Δωэ и интервал корре-
ляции τb и τk .
39. Найдите и изобразите функцию корреляции Kx (τ) стационарного случайного процесса X (t) со спектральной плотностью мощности Gx (ω) = G0 при −ω1 < ω< ω1 . Определите также интервал корреляции τ0 и τk .
40. Покажите, что корреляционная функция Kx (τ) не изменяется при добавлении к случайному процессу X (t) детерминирован-
ной составляющей a .
41. Заданы корреляционные функции:
а) K (τ) = D /(1+ a2τ2 ) ; б) K (τ) = D exp(−a2τ2 ) ;
в) K (τ) = D[sin(aτ)]/(aτ) .
Изобразите эти функции и рассчитайте интервал корреляции τb , τk (и τ0 для функции “в”), а также эффективную ширину спектра Δωэ .
42. Для стационарного случайного процесса
X (t) = Asin(ω0t + ϕ) ,
где ϕ – случайная величина, определите корреляционную функцию
как усреднением по ансамблю реализаций, так и по одной реализации на большом интервале наблюдения T . Является ли процесс X (t)
эргодическим по отношению к корреляционной функции?
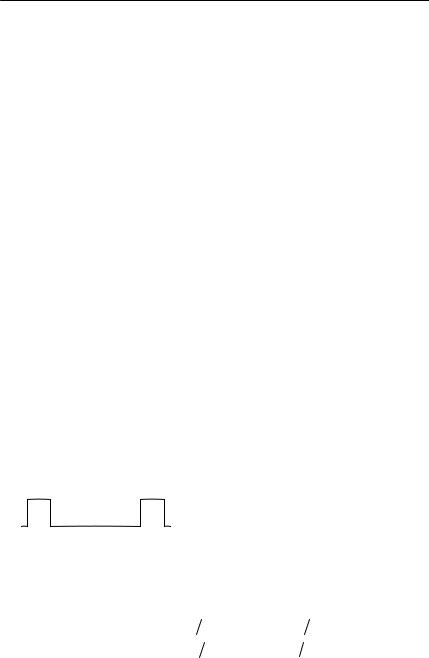
43.Найдите корреляционную функцию K (τ) и спектральную плотность мощности G(ω) “телеграфного сигнала”, заданного в задаче 24 (рис. 4.5). Изобразите графики K (τ) и G(ω) .
44.По результатам предыдущей задачи рассчитайте интервал корреляции τb и τk , а также эффективную ширину спектра Δωэ .
45.Определите корреляционную функцию процесса
N
X (t) = ∑[ An cos(ωnt) + Bn sin(ωnt)],
n=1
где ωn – известные частоты, а вещественные случайные величины An и Bn взаимно не коррелированы, имеют нулевые математиче-
ские ожидания и дисперсии D( A ) = D(B ) = σ2 |
, n = |
|
. |
||
1, N |
|||||
n |
n |
n |
|
|
|
85
4.3.5.УЗКОПОЛОСНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
46.Задан нормальный узкополосный случайный процесс
X (t) = A(t)sin[ω0t + ϕ(t)] , |
(*) |
где A(t) и ϕ(t) – медленные функции по сравнению с |
sin(ω0t) . |
Дисперсия Dx = σ2x =1 B2 . Найдите вероятность того, что в фиксированный момент времени огибающая A(t) процесса X (t) превы-
сит уровень 2 В.
47. Для процесса вида ( ) выразите математическое ожидание ( mA ) и дисперсию ( DA ) огибающей через его среднеквадратиче-
ское значение ( σx ).
48.Определите, является ли процесс вида (*) эргодическим относительно математического ожидания mx .
49.Выразите корреляционную функцию Kx (τ) процесса вида ( ) через известную функцию корреляции KA (τ) огибающей A(t) ,
приняв ϕ(t) = ϕ0 .
50. Найдите спектральную плотность мощности Gx (ω) узкополосного случайного процесса X (t) , если его корреляционная функция имеет вид
Kx (τ) = σ2xe−ατ cos(ω0τ) .
Изобразите графики Kx (τ) и Gx (ω) .
51. По условию предыдущей задачи найдите и графически изобра-
зите АКФ KA (τ) |
и СПМ GA (ω) огибающей |
A(t) |
случайного про- |
||||||||||
|
|
|
G (ω) |
|
|
|
|
|
|
цесса X (t) . |
Рассчитайте интервал |
||
|
|
|
|
|
|
|
|
|
корреляции τk и эффективную ши- |
||||
|
|
|
|
|
|
|
|||||||
|
|
|
G0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Δω |
|
рину спектра Δωэ |
огибающей A(t) , |
|||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
если σx = 1 В, α = 104 1/с. |
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
−ω0 |
0 |
|
ω0 |
ω |
||||||||
|
|
52. Найдите |
корреляционную |
||||||||||
|
|
|
Рис. 4.8 |
|
|||||||||
|
|
|
|
функцию Kx (τ) |
процесса вида |
||||||||
X (t) , если спектральная плотность мощности равномерна в полосе частот Δω (рис. 4.8).
G0 , −ω0 − Δω 2 < ω< −ω0 + Δω 2, Gx (ω) = G0 , ω0 − Δω 2 < ω< ω0 + Δω 2,
0, при других ω.

86 |
ГЛАВА 4. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ |
Изобразите график Kx (τ) и определите интервал корреляции τ0 огибающей этой функции.
53. Определите эффективную ширину спектра стационарного узкополосного процесса X (t) по его корреляционной функции
Kx (τ) = Dx exp(−α2τ2 ) cos(ω0τ) .
4.4.КОНТРОЛЬНОЕ ЗАДАНИЕ
4.4.1.ВЕРОЯТНОСТЬ ПРЕВЫШЕНИЯ ЗАДАННОГО УРОВНЯ
На пороговую схему воздействует случайное напряжение, распределенное по нормальному закону
w(u) = |
|
1 |
exp |
−(u − m)2 |
/ 2σ2 . |
|
|
||||
|
σ |
2π |
|
|
|
|
|
|
|
Какова вероятность P срабатывания схемы в фиксированный момент времени (t1), если схема срабатывает (Uвых ="1") всякий раз, когда напряжение на ее выходе превышает пороговое значение Uп .
Параметры m и σ даны в табл. 4.1, а Uп – в табл. 4.2.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4 . 1 |
|
||||
Параметр |
|
|
|
|
|
|
|
Номер варианта |
|
|
|
|
|
|
|
|
|
|||||
0 |
1 |
2 |
3 |
4 |
5 |
|
6 |
7 |
|
8 |
9 |
|
||||||||||
m , B |
–0.5 |
0 |
0.5 |
1.0 |
1.5 |
|
–0.5 |
|
0 |
0.5 |
|
1.0 |
1.5 |
|
||||||||
σ, B. |
1.0 |
1.0 |
1.0 |
1.0 |
1.0 |
2.0 |
|
2.0 |
2.0 |
|
2.0 |
2.0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4 . 2 |
|
||||
Параметр |
|
|
|
|
|
|
|
|
Номер варианта |
|
|
|
|
|
|
|
|
|||||
|
0 |
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
|
8 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Uп , B |
|
–2.0 |
|
–1.5 |
|
–1.0 |
|
–0.5 |
|
0 |
|
0.5 |
|
1.0 |
|
1.5 |
|
2.0 |
|
2.5 |
|
|
МЕТОДИЧЕСКОЕ УКАЗАНИЕ
При решении задачи можно воспользоваться значениями табулированного интеграла вероятности, приведенного в приложении П.7 (см. табл. П.4).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
87 |
4.4.2. |
ЗАКОН РАСПРЕДЕЛЕНИЯ |
|
|
|
|
|
|
|
|
|
|
|
||||||||
Стационарный случайный процесс U (t) описан плотностью |
||||||||||||||||||||
вероятности w(u) |
|
(табл. 4.3); параметры функции w(u) |
приведены |
|||||||||||||||||
в табл. 4.4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Требуется: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) получить выражение для функции распределения F (u) ; |
||||||||||||||||||||
б) построить график F (u) ; |
|
|
|
|
|
|
|
|
||||||||||||
в) |
найти выражение для характеристической функции θ(v) и |
|||||||||||||||||||
энтропии Н. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
МЕТОДИЧЕСКОЕ УКАЗАНИЕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Характеристики и параметры различных законов распределения |
||||||||||||||||||||
приведены в [8, 9], а нормального закона – в прил. П.7. |
Таблица 4 . 3 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
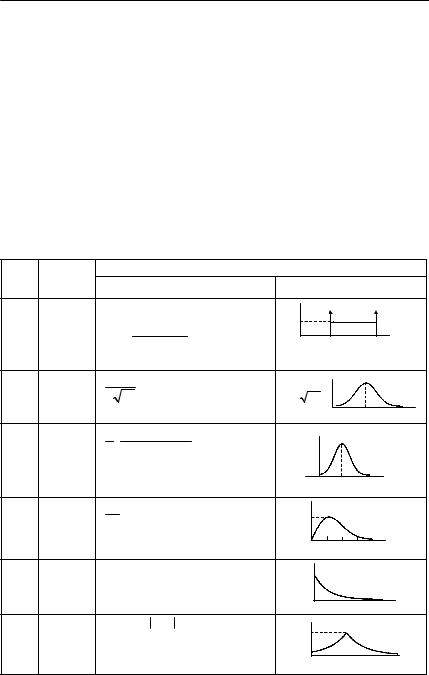
Номер Закон |
|
|
|
|
|
|
|
|
|
|
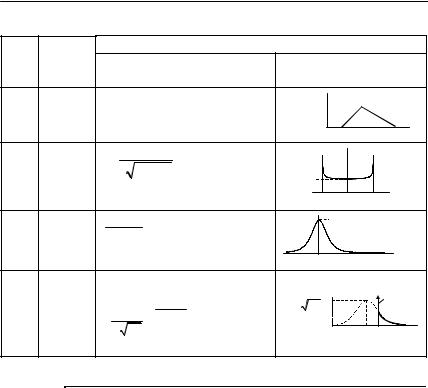
Плотность вероятности w(u) |
|
|
|
||||||
вариараспре- |
|
|
|
|
Аналитическая запись |
|
График |
|
||||||||||||
нта |
деления |
|
|
|
|
|
|
|||||||||||||
1 |
Равно- |
K δ(t − a), u = a, |
|
w(u) |
K δ (a) |
K δ (b) |
||||||||||||||
|
мерный |
|
C |
|
1 |
|
2 |
|||||||||||||
|
|
|
1 |
|
|
1 − K |
− K |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2 , a < u < b, |
|
|
|
|
|
||||||||
|
|
C = |
|
1 |
|
|
|
|
a |
b |
u |
|||||||||
|
|
|
|
|
δ(t |
b − a |
|
|
|
|
|
|
0 |
|||||||
|
|
K |
−b), u = b |
|
|
|
|
|
|
|
||||||||||
2 |
Нор- |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
w(u) |
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
||||
|
мальный |
σ |
|
2π e−(u−m) |
|
/ 2σ |
|
, |
1/ 2πσ |
|
|
|
||||||||
|
(Гаусса) |
−∞ < u < ∞ |
|
|
|
|
|
|
|
|
0 |
|
m |
u |
||||||
3 |
Коши |
|
|
|
|
|
|
|
w(u) |
|
||||||||||
1 |
|
|
|
|
|
h |
|
|
|
|
, |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
π |
|
h2 + (u −Uo )2 |
|
|
|
1/(πh) |
|
|
|
|
||||||||
|
|
−∞ < u < ∞ |
|
|
|
|
|
|
|
|
|
Uo |
|
u |
||||||
4 |
Релея |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||
u |
|
e |
−u2 |
/ 2σ2 |
, 0 |
< u < ∞ |
w(z) |
|
|
z = u / σ |
||||||||||
|
|
σ2 |
|
|
|
0.6 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
z |
5 |
Экспо- |
λe−λu , |
0 < u < ∞ |
|
|
|
w(u) |
|
|
|
|
|||||||||
|
ненци- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ |
|
|
|
|
|
альный |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
Лапласа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
u |
(λ/ 2)e−λ u−Uo |
, −∞ < u < ∞ |
w(u) |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
Uo |
u |
|
88 |
|
ГЛАВА 4. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ |
||||||||||||
|
|
|
|
|
|
|
|
|
Окончание табл. 4 . 3 . |
|||||
Но- |
Закон |
|
|
|
|
|
|
Плотность вероятности w(u) |
|
|
|
|||
мер |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
распре- |
|
|
Аналитическая запись |
|
|
График |
|
|
||||||
вари- |
деления |
|
|
|
|
|
|
|||||||
анта |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
Симпсо- |
|
|
|
|
|
2 |
,a < u < (a + b) / 2, |
w(u) |
|
|
|
|
|
|
на (тре- |
4(u − a) /(b − a) |
|
2 /(b |
− a) |
|
|
|
|
|||||
|
|
|
|
|
|
|
,(a + b) / 2 < u < b |
|
|
|
|
|||
|
уголь- |
4(b −u) /(b − a)2 |
|
|
|
|
|
|
||||||
|
ный) |
|
|
|
|
|
|
|
|
0 |
|
|
b |
u |
|
|
|
|
|
|
|
|
|
a |
|
||||
8 |
Аркси- |
|
|
|
1 |
, −a < u < a |
|
w(u) |
|
|
|
|||
|
нуса |
|
π |
a2 |
|
|
|
|
|
|
||||
|
|
|
−u2 |
|
|
1/(рa) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
9 |
|
|
|
|
|
|
|
|
|
−a |
0 |
a |
u |
|
|
|
a |
|
, −∞ < u < ∞ |
w(u) |
a / 2 |
|
|
||||||
|
|
2ch2au |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
Усечен- |
|
|
|
|
|
|
|
|
0 |
|
|
u |
|
Kδ(a), |
u = a, |
|
|
w(u) |
|
|
|
|
||||||
|
ный |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нормаль- |
|
1 |
|
−(u−m)2 |
1/ |
2ру |
|
|
Kд(a) |
||||
|
ный |
|
e |
2σ2 |
|
, a < u < ∞, |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
σ |
|
2π |
|
|
|
|
|
0 |
m a |
u |
||
|
|
K = φ[(a − m) / σ] |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4 . 4 |
||
Параметр |
|
|
|
Номер подварианта |
|
|
|
|||
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
K1 |
0.0 |
0.1 |
0.15 |
0.20 |
0.25 |
0.3 |
0.0 |
0.1 |
0.15 |
0.2 |
K2 |
0.31 |
0.25 |
0.20 |
0.15 |
0.10 |
0.0 |
0.0 |
0.1 |
0.10 |
0.2 |
a , B |
0.2 |
0.4 |
0.60 |
0.80 |
1.00 |
1.2 |
1.4 |
1.6 |
1.80 |
2.0 |
b , B |
1.2 |
1.6 |
2.00 |
2.40 |
2.80 |
3.2 |
3.6 |
4.0 |
4.40 |
4.8 |
m , B |
0.0 |
0.0 |
0.00 |
0.50 |
0.50 |
0.5 |
1.0 |
1.0 |
1.00 |
2.0 |
σ , B |
0.5 |
1.0 |
2.00 |
0.50 |
1.00 |
2.0 |
0.5 |
1.0 |
2.00 |
2.0 |
h , B |
0.5 |
1.0 |
2.00 |
0.50 |
1.00 |
2.0 |
0.5 |
1.0 |
2.00 |
2.0 |
U0 , B |
0.0 |
0.0 |
0.00 |
0.50 |
0.50 |
0.5 |
1.0 |
1.0 |
1.00 |
2.0 |
λ , 1/B |
0.5 |
1.0 |
1.50 |
2.00 |
2.50 |
3.0 |
3.5 |
4.0 |
4.50 |
5.0 |
α , B |
5.0 |
4.5 |
4.00 |
3.50 |
3.00 |
2.5 |
2.0 |
1.5 |
1.00 |
0.5 |
4.4.3. МОМЕНТНЫЕ ФУНКЦИИ. СТАЦИОНАРНОСТЬ И ЭРГОДИЧНОСТЬ
В табл. 4.5 задан процесс Z (t) . При описании Z (t) приняты следующие обозначения:

89
|
S1(t) и |
S2 (t) |
– детерминированные функции времени, описы- |
|||||
ваемые с помощью постоянных параметров S0 , |
α , ω0 , p , τ и n |
|||||||
(табл. 4.5); |
|
|
|
|
|
|
||
|
X и Y |
– некоррелированные случайные величины с известны- |
||||||
ми |
математическими ожиданиями mx |
и my |
и дисперсиями |
|||||
D = σ2 |
и D |
y |
= σ2 ; |
|
|
|||
x |
x |
|
|
|
y |
|
|
|
|
X (t) |
и |
Y (t) |
– некоррелированные |
эргодические случайные |
|||
процессы, которые соответственно имеют известные математические ожидания mx и my дисперсии Dx = σ2x и Dy = σ2y и автокорреляционные функции Kx (τ) и K y (τ) .
Требуется: |
|
|
|
mz (t) , дисперсию |
|||
а) |
определить математическое ожидание |
||||||
Dz (t) |
и корреляционную функциюKz (t1,t2 ) процесса Z (t) ; |
||||||
б) |
классифицировать процесс |
Z (t) по признакам стационарно- |
|||||
сти и эргодичности. |
|
|
|
|
Таблица 4 . 5 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер |
|
Номер |
|
|
|
|
|
Z (t) |
под- |
|
S1(t) |
|
S2 (t) |
||
вариан- |
|
|
|||||
вари- |
|
|
|||||
та |
|
|
|
|
|
|
|
|
|
анта |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
XS1(t) |
0 |
|
S0at |
|
S0 exp(−β2t2 ) |
1 |
|
XS1(t) + Y |
1 |
|
S0 sin ω0t |
|
S0[1 − exp(−at)] |
2 |
|
X (t) + S1(t) |
2 |
|
S0 (at)2 |
|
S0 exp(−at) |
3 |
|
XS1(t) + YS2 (t) |
3 |
|
S0 cos ω0t |
|
S0[exp(−at)]n |
4 |
|
X + YS2 (t) |
4 |
|
S0 / at |
|
S0 cos ω0t |
5 |
|
S2 (t) +Y (t) |
5 |
|
S0[exp(−at)]n |
|
S0at |
6 |
|
Y sin ω0t + S2 (t) |
6 |
|
S0 exp(−β2t2 ) |
|
S0 (at)2 |
7 |
|
XS2 (t) |
7 |
|
S0 exp(−at) |
|
S0 sin ω0t |
8 |
|
XS1(t) |
8 |
|
S0 ,0 < t < τ |
|
S0 / at |
9 |
|
Y (t) + S1(t) |
9 |
|
S0[1 − exp(−at)] |
|
S0 ,0 < t < τ |
Ваша идея, конечно, безумна.
Весь вопрос в том, достаточно ли она безумна, чтобы оказаться правильной.
Нильс Бор
ГЛАВА 5
ЛИНЕЙНЫЕ ЦЕПИ
5.1.ИЗУЧАЕМЫЕ ВОПРОСЫ
Частотные и временные характеристики линейных систем. Ма-
тематические модели апериодических и частотно-избирательных линейных цепей. Свойства цепей с обратной связью (ОС). Критерии устойчивости активных линейных цепей с ОС (алгебраические и геометрические). Гребенчатые фильтры. [1, 5.7…5.10; 2, 14.1, 14.2; 3, 5.8…5.11].
Указания. При изучении линейных цепей надо обратить внимание на то, что передаточная функция K(jω) любой системы, в том числе с обратной связью, записывается в виде правильной дроби, т. е. в виде отношения двух степенных полиномов комплексной переменной jω. Такая запись существенно упрощает исследование цепей и позволяет применить универсальные типовые методы.
При рассмотрении частотных свойств необходимо чётко уяснить поведение АЧХ и ФЧХ минимально-фазовых и неминималь- но-фазовых цепей. Следует внимательно разобраться, почему цепи с распределёнными параметрами, например устройства, содержащие отрезки линий передач, относятся к классу неминимально– фазовых цепей. Существенной особенностью всех физически реализуемых цепей является отсутствие разрывов частотной зависимости ФЧХ.
При определении устойчивости важно уметь записывать комплексные передаточные функции каскадно-соединённых пассивных и активных усилительных элементов. Отметим также, что в активных цепях с обратной связью в одной области частот обратная связь может быть отрицательной, а в другой – положительной.
