
ТОИИТ / Задания
.pdf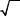
|
21 |
24. Сигнал u (t) =1t2 |
, 0 ≤ t ≤1 аппроксимирован линейной |
1 |
|
функцией u2 (t) = at + b . Найдите коэффициенты a и b , потребовав наименьшей метрики d (u1(t),u2 (t)) .
25. Заданы два экспоненциальных видеоимпульса, смещенных на величину t0
u1(t) =Ue−αt σ(t) , u2 (t) =Ue−α(t−t0 )σ(t −t0 ) .
Найдите зависимость угла ψ1,2 между векторами от параметра t0 .
Найдите значение t0 , при котором ψ1,2 = 89o , т. е. видеоимпульсы
практически ортогональны.
26. Покажите, что комплексные экспоненциальные функции
|
1 |
|
|
2π |
|
|
|
|
ϕn (t) = |
|
exp |
j |
|
nt |
, |
n = 0, ±1, ± 2,... |
|
T |
T |
|||||||
|
|
|
|
|
|
на интервале −T / 2 ≤ t ≤T / 2 образуют ортонормированный базис. 27. Докажите, что в вещественном гильбертовом пространстве, содержащем сигналы U и V , справедливо равенство параллело-
грамма:

 U +V
U +V 
 2 +
2 + 
 U −V
U −V 
 2 = 2
2 = 2 
 U
U 
 2 + 2
2 + 2 
 V
V 
 2 .
2 .
28. Докажите, что в комплексном гильбертовом пространстве, содержащем сигналы U и V , имеет место тождество
4(U ,V ) = 
 U +V
U +V 
 2 +
2 + 
 U −V
U −V 
 2 + j
2 + j 
 U + jV
U + jV 
 2 − j
2 − j 
 U − jV
U − jV 
 2 .
2 .
1.3.4.ПРЕДСТАВЛЕНИЕ СИГНАЛОВ В БАЗИСЕ ФУНКЦИЙ УОЛША
29.Сформируйте с помощью матриц Адамара функции Уолша (ФУ) при базисе: а) N = 4, б) N = 8, в) N = 16. Упорядочите
функции по Адамару и Уолшу.
30. Перемножение двух ФУ дает также ФУ: wal(k, θ) wal(i, θ) = wal(m, θ) .
Определите номер m i = 7 ; б) k =8, i = 5 ; в)
результирующей функции, если: а) k =3, k = 6, i =12 .
31. Дана периодическая последовательность прямоугольных импульсов с амплитудой S0 , длительностью τu и периодом повто-
рения Т

22 |
ГЛАВА 1. ЭЛЕМЕНТЫ ОБЩЕЙ ТЕОРИИ СИГНАЛОВ |
S(t) = So , 0 ≤ t ≤ τu .
Определите спектр в базисе ФУ на интервале [0, T] для следующих значений скважности ( q =T / τu ): а) 2; б) 4; в) 8.
32. Сигнал S1(θ) имеет спектр {B1,n} = B0,1,...., B1,n . Чем отличается спектр сигнала S2 (θ) , связанного с сигналом S1(θ) соотноше-
нием: а) S2 (θ) = S0S1(θ) ; б) S2 (θ) = S0 + S1(θ) ; в) S2 (θ) = S0 − S1(θ) ? 33. Как изменится спектр меандра ( τu = T / 2 ) при задержке на
τз = τи / 2 ?
34. Один период Т колебания треугольной формы S(θ) = S0θ, при 0 ≤ θ = t / T ≤1 аппроксимируется пятью членами ряда:
S%(θ) = S20 wal(0, θ) − S40 wal(1, θ) −
− S80 wal(3, θ) − 16So wal(7, θ) − 32S0 wal(15, θ)
Определите энергию и среднюю мощность колебания S%(θ) (на со-
противлении 1 Ом) и сравните полученные значения с энергией и мощностью исходного колебания S(θ) . Sо =1 В, Т = 1 мс.
35. По данным предыдущей задачи изобразите аппроксимированный (синтезированный) сигнал S%(θ) и определите относительную среднеквадратическую ошибку аппроксимации μ для случаев,
когда S%(θ) содержит: а) два члена ряда ( N = 2), б) три члена ( N = 4), в) четыре члена ( N = 8), г) пять членов ( N = 16). Амплитуду S0 принять равной 32 В.
36.Определите спектр и постройте спектральную диаграмму сигнала S(θ) , приведенного в табл. 1.1, в базисе 4 (8 или 16) ФУ.
37.По результатам предыдущей задачи синтезируйте сигнал на интервале [0,1] и постройте на одном графике исходный S(θ) и
синтезированный S%(θ) сигналы.
38. По данным задач 36 и 37 рассчитайте норму и энергию (при R = 1 Ом) исходного и синтезированного сигналов и определите относительную среднеквадратическую ошибку аппроксимации (синтеза).
|
|
|
|
|
|
|
|
|
|
23 |
|
|
|
|
|
|
|
|
|
|
Таблица 1 . 1 |
Номер- |
|
|
|
Сигнал S (θ) |
|
|
||||
вари- |
|
График |
|
|
|
|
|
|
Аналитическая запись |
|
анта |
|
|
|
|
|
|
|
|||
1 |
S 0 |
|
|
|
|
S0 , |
0 ≤ и≤1/ 4, |
|||
|
|
|
1 .0 |
|
||||||
|
|
|
|
−S0, |
3/ 4 ≤ и≤1.0 |
|||||
|
0 |
0 .5 |
|
и |
|
|||||
2 |
S0o/2 |
|
|
|
S0и, |
0 ≤ и≤ 0.5, |
||||
|
|
1.0 |
||||||||
|
|
|
|
S0 (и−1), |
0.5 ≤ и≤1.0 |
|||||
|
0 |
0.5 |
|
θи |
|
|||||
|
|
|
|
|
|
|
|
|||
3 |
S0/2 |
|
|
θи |
S0 (и−0.5), |
0 ≤ и≤1 |
||||
|
0 |
0.5 |
1.0 |
|||||||
|
|
|
|
|
|
|
|
|||
4 |
S0o |
|
|
|
2S0θ, |
0 ≤ и≤ 0.5, |
||||
|
|
|
|
|||||||
|
|
|
|
|
||||||
|
0 |
|
|
θ |
|
|
|
|
−и), |
0.5 ≤ и≤1.0 |
|
0.5 |
1.0 |
2S0 (1 |
|||||||
|
|
и |
|
|
|
|
|
|
||
5 |
S0/2 |
|
|
|
S0 (0.5и− 2θ), 0 ≤ и≤ 0.5, |
|||||
|
0.5 |
|
|
|||||||
|
|
|
|
|
|
(2и−1.5), 0.5 ≤ и≤1.0 |
||||
|
0 |
|
1.0 θи |
S0 |
||||||
|
|
|
|
|
|
|
|
|||
6 |
So |
|
|
|
S0 (1 − 4и), |
0 ≤ и≤ 0.25, |
||||
|
|
|
|
|||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.25 ≤ и≤ 0.75, |
||
|
|
|
|
|
0, |
|
||||
|
0 |
0.5 |
1.0 |
θи |
4S |
0 |
(и− 0.75), 0.75 ≤ и≤1.0 |
|||
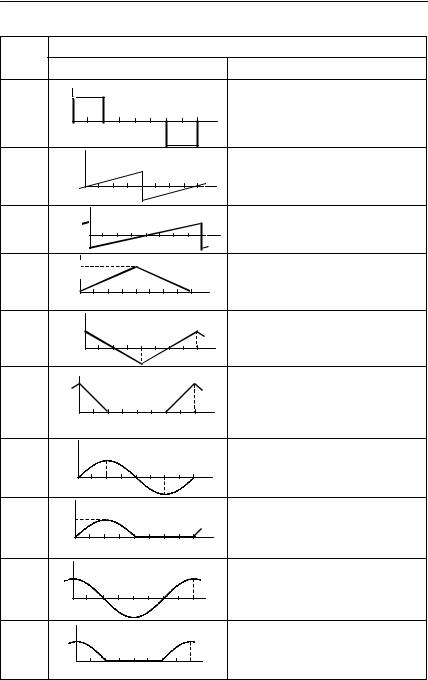
7 |
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
1.0 |
|
Asin(2πθ), 0 ≤ θ ≤1 |
||||||
|
|
|
|
|||||||
|
0 |
0.5 |
|
иθ |
|
|
|
|
|
|
8 |
А |
|
|
|
Asin(2πθ), |
0 ≤ θ ≤ 0.5, |
||||
|
|
|
|
|
||||||
|
|
|
|
θ |
|
|
0.5 ≤ θ ≤1.0 |
|||
|
0 |
0.5 |
1.0 |
0, |
||||||
|
и |
|
|
|
|
|
|
|||
9 |
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
иθ |
Acos(2πθ), |
0 ≤ θ ≤1 |
||||
|
0 |
0.5 |
1.0 |
|
|
|
|
|
|
|
10 |
А |
|
|
|
Acos(2πθ), |
0 ≤ θ ≤ 0.25, |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, 0.25 ≤ θ ≤ 0.75, |
|||||
|
0 |
0.5 |
1.0 |
θи |
Acos(2πθ), |
0.75 ≤ θ ≤1.0 |
||||
24 |
|
|
|
ГЛАВА 1. ЭЛЕМЕНТЫ ОБЩЕЙ ТЕОРИИ СИГНАЛОВ |
||||
|
|
|
|
|
|
|
Окончание табл. 1 . 1 |
|
|
|
|
|
|
|
|
|
|
Номер- |
|
|
|
Сигнал S (θ) |
||||
вари- |
|
|
|
|
|
|
|
|
|
|
График |
|
|
|
Аналитическая запись |
||
анта |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
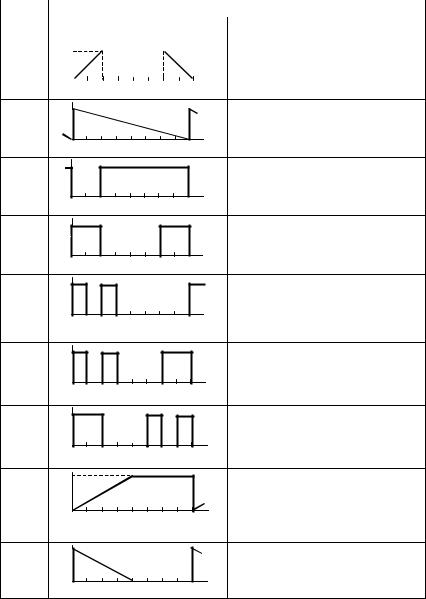
11 |
S |
|
|
|
|
|
4S0 и, 0 ≤ и≤ 0.25, |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||
|
So0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S0 , 0.25 ≤ и≤ 0.75, |
|
|
0 |
0.5 |
1.0 |
иθ |
S0[1 − 4(и− 0.75)],0.75 ≤ и≤1.0 |
|||
12 |
S0o |
|
|
|
S0 (1−и), 0 ≤ и≤1.0 |
|||
|
|
|
|
θ |
||||
|
0 |
0.5 |
1.0 |
|
|
|
|
|
|
и |
|
|
|
|
|||
13 |
S0 |
|
|
|
0, 0 ≤ и≤ 0.25, |
|||
|
|
|
|
θ |
|
|
, |
0.25 ≤ и≤1.0 |
|
0 |
0.5 |
1.0 |
S0 |
||||
|
и |
|
|
|
|
|||
14 |
SSo0 |
|
|
|
S0 , 0 ≤ и≤ 0.25, |
|||
|
|
|
|
|||||
|
|
|
|
|
0, |
|
0.25 ≤ и≤ 0.75, |
|
|
0 |
0.5 |
1.0 |
θ |
|
|
, |
0.75 ≤ и≤1.0 |
|
и |
S0 |
||||||
15 |
SSo0 |
|
|
|
S0 , 0 ≤ и≤ 0.125, |
|||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
0.25 ≤ и≤ 0.375, |
|
|
|
|
иθ |
|
|
|
|
|
0 |
0.5 |
1.0 |
|
|
|
вне этих интервалов |
|
|
|
|
|
|
0, |
|
||
16 |
S0 |
|
|
|
S0 , 0 ≤ и≤1/ 8, 2 / 8 ≤ и≤ 3/ 8 |
|||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
6 / 8 ≤ и≤1/ 0, |
|
|
|
|
иθ |
|
|
|
|
|
0 |
0.5 |
1.0 |
0, |
|
вне этих интервалов |
||
17 |
S0 |
|
|
|
S0 , 0 ≤ и≤1/ 4, 5 / 8 ≤ и≤ 6 / 8 |
|||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
7 / 8 ≤ и≤1/ 0, |
|
|
|
|
θ |
|
|
|
|
|
0 |
0.5 |
1.0 |
|
|
|
вне этих интервалов |
|
|
и |
0, |
|
|||||
18 |
So |
|
|
|
2S0θ, 0 ≤ и≤ 0.5, |
|||
|
|
|
|
|
||||
|
0 |
0.5 |
1.0 |
θ |
S |
0 |
, |
0.5 ≤ и≤1.0 |
|
и |
|
|
|
||||
19 |
So |
|
|
|
S0 (1− 2и), 0 ≤ и≤ 0.5, |
|||
|
|
|
|
|
||||
|
|
|
|
θ |
|
|
|
0.5 ≤ и≤1.0 |
|
0 |
0.5 |
1.0 |
0, |
|
|||
|
и |
|
|
|
|
|||

25
20 |
So |
|
|
|
|
0 |
0.5 |
1.0 |
θ |
|
и |
S0 , 0 ≤ и≤1/ 8, 3/ 8 ≤ и≤ 5 / 8 |
||
|
|
7 / 8 ≤ и≤1.0, |
|
|
|
|
0, |
вне этих интервалов |
|
||
26 |
ГЛАВА 1. ЭЛЕМЕНТЫ ОБЩЕЙ ТЕОРИИ СИГНАЛОВ |
1.4.КОНТРОЛЬНОЕ ЗАДАНИЕ
1.4.1.МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИГНАЛА
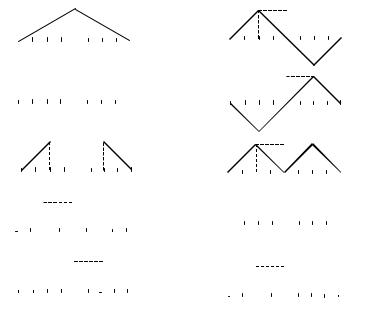
Втабл. 1.2 и 1.3 заданы варианты и подварианты импульсного сигнала.
Требуется:
Записать математическую модель сигнала S(t) через временные
интервалы и на непрерывной оси времени с помощью комбинаций (суммы и произведений) функций Хевисайда.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1 . 2 |
||||||||
Ва- |
|
|
|
|
|
|
|
Сигнал S(t) |
|
|
|
|
|
|
|
|
|
|
Ва- |
|
|
|
|
|
|
|
Сигнал S(t) |
|
|
|
|
|
||||||||||||||||
риант |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
риант |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
ф/ 2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−ф/ 2 |
|
|
|
|
|
|
|
|
|
|
|
t |
||||||
|
|
|
−ф/ 2 |
|
|
|
|
|
|
|
|
|
|
ф/ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
−ф/ 2 |
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
−ф/ 2 |
|
|
U |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
-U |
ф/ 2 |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
ф/ 2 |
t |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
−ф/ 2 |
|
|
|
|
|
|
|
|
|
|
ф/ 2 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
−ф/ 2 |
|
|
0 |
|
ф/ 2 t |
|||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
ф/ 2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−ф/ 2 |
|
|
|
|
|
0 |
|
|
|
|
t |
|
|||||||
|
|
|
−ф/ 2 |
|
|
|
0 |
|
|
|
|
|
|
ф/ 2 |
|
t |
|
|
|
|
|
|
-U |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4 |
|
−ф/ 2 |
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
ф/ 2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
ф/ 2 t |
|
|
|
|
|
− |
ф/ 2 |
|
|
0 |
|
|
|
|
t |
|||||||||||||||||
|
|
|
|
|
|
|
|
-U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-U |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1 . 3 |
||||||||
Подвариант |
0 |
|
|
1 |
|
|
|
|
|
2 |
|
3 |
|
|
|
4 |
|
5 |
|
|
6 |
|
7 |
|
8 |
|
|
9 |
|
|
||||||||||||||||||
U, B |
10 |
|
8 |
|
|
|
|
|
4 |
|
2 |
|
|
|
1 |
|
10 |
|
|
8 |
|
4 |
|
2 |
|
|
1 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
τ,мс |
1 |
|
|
2 |
|
|
|
|
|
3 |
|
4 |
|
|
|
5 |
|
5 |
|
|
4 |
|
3 |
|
2 |
|
|
1 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Т, мс |
3 |
|
|
6 |
|
|
|
|
|
9 |
|
12 |
|
15 |
|
20 |
|
|
16 |
|
12 |
|
8 |
|
|
4 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27
1.4.2. ПРЕДСТАВЛЕНИЕ СИГНАЛА В БАЗИСЕ ФУНКЦИЙ УОЛША
Аппроксимируйте сигнал S(θ) в базисе 8 ФУ wal(n,θ) , n =
0,...,7. Форма сигнала задана в табл.1.4, а параметры приведены в табл.1.5.
Требуется:
а) определить спектр и построить спектральную диаграмму для
заданного θo и θo = 0 ;
б) синтезировать сигнал на интервале [0, 1] и построить на одном графике заданную и аппроксимированную функцию для θo = 0 ;
в) рассчитать норму и энергию (на сопротивлении 1 Ом) исходного и аппроксимированного сигнала;
г) определить относительную среднеквадратическую ошибку аппроксимации.
Таблица 1 . 4
Ва- |
|
|
|
|
|
Сигнал S (θ) |
риант |
|
|
График |
|
|
Аналитическая запись |
|
|
|
|
|
||
0 |
А |
|
|
|
|
|
|
0 |
и0 |
0.5 |
1.0 |
и |
Acos[2π(θ−θ0)] |
|
|
|||||
1 |
А |
и0 |
|
|
|
|
|
|
|
|
и |
Asin[2π(θ −θ0 )] |
|
|
0 |
|
0.5 |
1.0 |
||
|
|
|
||||
2 |
S0 |
|
|
|
|
S0 (θ+1− θ0 ), 0 ≤ θ ≤ θ0, |
|
|
|
|
|
|
|
|
0 |
и0 |
0.5 |
1.0 |
и |
S0 (θ− θ0 ), θ0 ≤ θ ≤1.0 |
|
|
|||||
3 |
S0 |
|
|
|
|
S0 (θ0 − θ), 0 ≤ θ ≤ θ0, |
|
|
|
|
|
|
|
|
0 |
и0 |
0.5 |
1.0 |
и |
S0[1 − (θ − θ0 )], θ0 ≤ θ ≤1.0 |
|
|
4 |
S0 |
|
|
|
|
|
2S0 (θ0 − θ), 0 ≤ θ ≤ θ0 , |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2S0 (θ − θ0 ), θ0 ≤ θ ≤ θ0 + 0.5, |
||
|
0 |
и |
0.5 |
1.0 и |
|
|
|
0.5 + θ0 ≤ θ ≤1.0 |
|
|
|
|
0 |
|
|
|
2S0[1 − (θ − θ0 )], |
||
5 |
S0 |
|
|
|
|
|
S0 (1 − 2(θ0 − θ)], |
0 ≤ θ ≤ θ0 , |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S0 |
(1 − 2(θ − θ0 )], |
θ0 ≤ θ ≤ θ0 + 0.5, |
|
0 |
и |
0.5 |
1.0 и |
|
[2(θ − θ0 ) −1], |
0.5 + θ0 ≤ θ ≤1.0 |
||
|
|
|
0 |
|
|
|
S0 |
||
Окончание табл. 1 . 4
28 |
|
ГЛАВА 1. ЭЛЕМЕНТЫ ОБЩЕЙ ТЕОРИИ СИГНАЛОВ |
||
|
|
|
|
|
Ва- |
|
Сигнал S (θ) |
||
риант |
|
|
|
|
График |
Аналитическая запись |
|||
|
||||
6 |
S0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
0 |
, θ |
0 |
≤ θ ≤ θ + θ , θ =1/ 4, |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 и |
и |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
вне этого интервала |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
0 |
|
и0 |
0.5 |
|
|
|
1.0 |
и |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
7 |
S0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
θ0 ≤ θ ≤ θ0 + θи, θи =1/ 4, |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S0 |
, |
вне этого интервала |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
0 |
и0 |
0.5 |
|
|
|
1.0 |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
8 |
S0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S0 , |
θ0 ≤ θ ≤ θ0 + θи, |
θи =1/8, |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S0 , θ0 + 2θu ≤ θ ≤ θ0 + 3θи, |
|
|
|
|||||||||
|
0 |
|
и |
0.5 |
|
|
|
1.0 |
|
|
и |
|
|
|
|
вне этих интервалов |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
9 |
S0/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−S0 / 2, θ0 ≤ θ ≤ θ0 + θи, θи =1/ 8, |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−S0 / 2, θ0 + 2θu ≤ θ ≤ θ0 + 3θи, |
|
|
||||||||||
|
0 |
|
|
|
|
|
0.5 |
|
1.0 |
и |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
S0 |
/ 2, |
|
вне этих интервалов |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
и0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1 . 5 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Подвариант |
|
0 |
1 |
|
|
2 |
3 |
|
|
4 |
|
5 |
6 |
|
7 |
|
8 |
9 |
|
|||||||||||||||||||
θ0 |
|
|
|
|
|
|
|
1/16 |
2/16 |
|
3/16 |
4/16 |
5/16 |
|
6/16 |
7/16 |
|
8/16 |
|
9/16 |
10/16 |
|
||||||||||||||||
А или |
|
10 |
9 |
|
|
8 |
7 |
|
|
6 |
|
5 |
4 |
|
3 |
|
2 |
1 |
|
|||||||||||||||||||
S0 , В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
О сколько нам открытий чудных Готовят просвещенья дух И опыт, сын ошибок трудных, И гений парадоксов друг …
Александр Пушкин
ГЛАВА 2
СПЕКТРАЛЬНЫЕ ФОРМЫ ПРЕДСТАВЛЕНИЯ СИГНАЛОВ
2.1. ИЗУЧАЕМЫЕ ВОПРОСЫ
Гармонический анализ периодических колебаний. Тригономет-
рическая и комплексная форма ряда Фурье. Спектр периодического колебания. Амплитудные и фазовые спектральные диаграммы. Связь тригонометрических и комплексных коэффициентов ряда Фурье. Энергетические характеристики периодических сигналов. Распределение энергии и мощности в спектре периодического сиг-
нала [1, 2.3…2.5; 2, 2.1; 3, 1.1, 1.2, 2.1].
Спектральное представление непериодических колебаний. Преобразование Фурье. Спектральная плотность. Связь между спектральной плотностью непериодического колебания и спектральными коэффициентами периодического колебания. Теоремы о спектрах. Энергетические характеристики непериодического колебания. Энергетический спектр. Равенство Парсеваля. Обобщенная формула Релея. Понятие активной (эффективной) длительности и ширины спектра непериодического сигнала; соотношение между
ними [1, 2.6…2.14; 2, 2.2-2.5; 3, 2.1…2.6].
Корреляционные функции детерминированных сигналов. Автокорреляционная функция (АКФ). Свойства АКФ, связь с энергетическим спектром сигнала. Взаимная корреляционная функция (ВКФ) и ее связь со взаимным энергетическим спектром [1, 2.18,
2.19; 2, 3.2; 3, 1.3, 2.2…2.4].
Представление сигналов рядом Котельникова. Теорема Котельникова. Дискретизация непрерывных сигналов. Интервал Найквиста. База сигнала. Спектр дискретизированного сигнала [1, 2.15…2.17; 3, 2.7; 2, 5.2].

30 |
ГЛАВА 2. СПЕКТРАЛЬНЫЕ ФОРМЫ ПРЕДСТАВЛЕНИЯ СИГНАЛОВ |
2.2.КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Представление периодического сигнала S (t) = S (t + nT0 ) или сигнала с ограниченной областью определения ( t1 <Tonp < t2 )
обобщенным рядом Фурье (1.13) в базисе основных тригонометрических функций ( sin 2πnt / T ; cos 2πnt / T ) называется гармониче-
ским. Такое представление возможно, если T =T0 или T =Tonp и имеет вид:
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
S(t) = a0 + ∑(an cos nω0t + bn sin nω0t) = |
|||||||||||||||||
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
(2.1) |
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
= A0 + ∑An cos(nω0t −ϕn ), |
|
||||||||||||
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
||
где ω0 = 2π/ T ; |
n =1,2,3,...; |
|
|
|
|
|
|
|
|||||||||
a |
= |
1 |
|
T |
S(t)dt |
; |
a |
= |
|
2 |
T S(t) cos(nω t)dt ; |
||||||
T |
|
∫ |
T |
||||||||||||||
0 |
|
|
|
|
|
|
|
n |
|
∫ |
|
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
b |
= |
2 |
|
T |
S(t)sin(nω t)dt ; |
(2.2) |
||||||
|
|
|
|
|
T |
|
∫ |
||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
A |
= a |
; |
A |
= |
a2 + b2 |
; ϕ |
n |
= arctg(b |
/ a ) . |
||||||||
o |
|
o |
|
|
n |
|
|
|
n |
n |
|
|
|
n |
n |
||
Совокупность коэффициентов An и ϕn образуeт дискретный
спектр периодического колебания. Изображение коэффициентов в координатах амплитуда – частота и фаза – частота называется со-
ответственно амплитудными и фазовыми спектральными диаграммами или амплитудным и фазовым спектром (рис. 2.1, а).
Кроме тригонометрической формы записи ряда Фурье часто используют комплексную форму. Она соответствует разложению сигнала S(t) в обобщенный ряд Фурье (1.13) по системе ортого-
нальных функций
e jnωot = cos nωot + j sin nωot ; n = 0,±1, ±2,...
и имеет вид
∞ |
& |
jnωot |
, |
(2.3) |
S(t) = ∑ Ce |
|
|||
n=−∞
где
