Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Институт информационных технологий БГУИР

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ТОИИТ / Задания

.pdf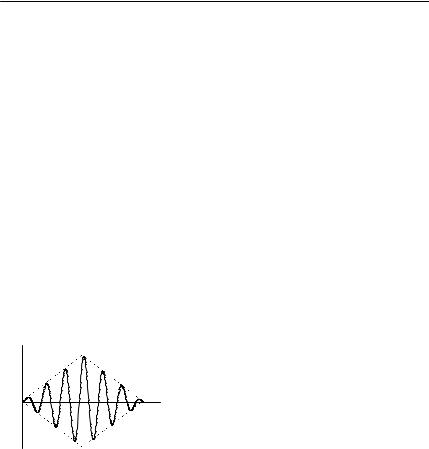

Скачиваний:

126

Добавлен:

24.02.2016

Размер:

9.82 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 3613 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

121

действием сигнала e(t) = Eσ(t)cos(ω0t) при наличии расстройки ω0 = ωp + Δω. Изобразите закон изменения амплитуды тока I(t) при различных расстройках ( ω = 0 , Δω1 , Δω2 > Δω1 ).

27.На одноконтурный резонансный усилитель подаётся периодическая последовательность импульсов высокой частоты с прямоугольной огибающей. Амплитуда импульсов 0.1 В, длительность 100 мкс, частота повторения 5 кГц, несущая частота равна резонансной частоте контура. Параметры усилителя: коэффициент усиления 40, резонансная частота 640 кГц, полоса пропускания 8 кГц.

Рассчитайте и постройте временные диаграммы тока в контуре

инапряжения на выходе усилителя.

28.На вход резонансного усилителя подано напряжение

u	вх	(t) =U	0	cos(2π 16 t) , 0 ≤ t ≤ τ			u	=1 мс.
	вх		0				u
Найдите полосу пропускания усилителя, если время установле-
ния колебаний на его выходе равно 0,1 мс. Что произойдёт с дли-
тельностью фронтов импульса на выходе, если полосу пропускания
усилителя увеличить (уменьшить) в два раза?
29. На входе последовательного колебательного контура действу-
e(t)					ет ЭДС в виде высокочастотного им-
e(t)					пульса	с		треугольной		огибающей
E					пульса	с		треугольной		огибающей
E					(рис. 6.15):			E =1	В,	τи =10	мкс,
					f0 = fp . Параметры контура:						L =10
0				τu t	мкГн,	C = 30 пФ,			Q =120 .
					Рассчитайте и постройте времен-
					ные диаграммы тока в контуре и на-
Рис. 6.15					пряжения на конденсаторе.
Рис. 6.15					30.	Какую добротность должен
					30.	Какую добротность должен
иметь контур, чтобы пропускать колебание с несущей частотой 100
МГц при частотном отклонении 50 кГц и модулирующей частоте 5
кГц? Ослабление крайних практически важных частот спектра не
должно превышать: а) 10 %, б) 30 %.
31. Частотно–модулированная ЭДС

e(t) = 0.1cos[2π 6 106 t + 6sin(2π 6 103 t)] В

действует на последовательный колебательный контур с добротностью Q =120 и резонансной частотой f p = f0 .

122	ГЛАВА 6. ПРОХОЖДЕНИЕ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ

Пользуясь методом “мгновенной” частоты, определите максимальное напряжение на конденсаторе контура, а также закон и па-

раметры ωвых(t) .

32.На резонансный усилитель с резонансной частотой 10 МГц и полосой пропускания 200 кГц подаётся ЧМ колебание, несущая частота которого 10 МГц, модулирующая частота 2 кГц, индекс модуляции 30.

С какой частотой изменяется амплитуда сигнала на выходе усилителя? Найдите коэффициент глубины модуляции выходного сигнала.

33.На вход резонансного усилителя с передаточной функцией

K ( jω) = K0 /[1+ j(ω−ωp ) / Δω0.7 ] подаётся импульсный ЛЧМ сигнал uвх(t) =Um cos(ω0t +βt2 / 2) , 0 ≤ t ≤ τи .

Параметры усилителя: K0 =100 , ωp =106 рад/с, Δω0.7 =104 рад/с, параметры сигнала: Um = 0.1B, ω0 = ωp , β =107 рад/с2, τи = 4 мс.

Определите закон изменения огибающей выходного импульса, а также закон изменения мгновенной частоты колебания в контуре

усилителя, сопоставив его с ωвх(t) .

34. На вход последовательного колебательного контура подключена ЭДС

e(t) = Ee−αt cos(ω0t + ϕ) , t ≥ 0 ,

гдеE =1 В,	α =104 1/с, ω = 2π 106	рад/с, ϕ = 450 . Параметры
	0
контура: ω = ω , полоса пропускания 2Δω0,7 = 2π104 рад/с.
р	0

Пользуясь приближённым спектральным методом, определите напряжение на конденсаторе (выходе) контура.

35. Определите ток в последовательном колебательном контуре с параметрами ωр =106 рад/с, Q =100 , L =1 мГн, на вход которого подано напряжение

e(t) =100 В, τи / 2 ≤ t ≤ τи / 2 .

Для решения задачи используйте приближённый спектральный метод.

36. На одноконтурный резонансный усилитель воздействует фазоманипулированное колебание со скачкообразным изменением

фазы на ϕ0 радиан при t = 0 :

123

cos(ω		p	t)		при t < 0,
		p
uвх(t) =Um	cos(ω		t + ϕ		) при t > 0.
	cos(ω	p	t + ϕ	0	) при t > 0.

124	ГЛАВА 6. ПРОХОЖДЕНИЕ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ

Используя приближённый метод интеграла положения, определите комплексную огибающую U&вых(t) и физическую огибающую Uвых(t) выходного сигнала при двух значениях фазового сдвига

ϕ0 : 900 и 1800. Изобразите зависимость Uвых(t / τк) , где τк – постоянная времени контура.

6.4.КОНТРОЛЬНОЕ ЗАДАНИЕ

6.4.1. ВОЗДЕЙСТВИЕ ИМПУЛЬСНЫХ СИГНАЛОВ НА АПЕРИОДИЧЕСКИЕ ЦЕПИ

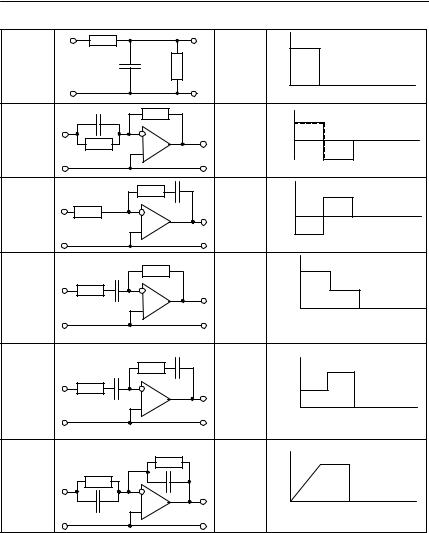
В табл. 6.2 приведены входное воздействие и структура цепи.

Требуется определить:

а) передаточную функцию цепи и построить АЧХ и ФЧХ; б) реакцию цепи на входное воздействие, построив график.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Рекомендуется использовать операторный метод. Для активной цепи задачу решить в общем виде, для пассивной – с подстановкой:

Е = 40 В, τи =10 мс.

					Таблица 6 . 2
Номер			Номер
Номер	Цепь		подва-	Воздействие
варианта	Цепь		подва-	Воздействие
варианта			рианта
			рианта
	R=100 Ом	C=10-5	Ф	E
0	R=100 Ом	C=10-5	Ф
0			0
				ф		t
				E
1	C=10-5 Ф		1
	R=100 Ом			ф		t
				ф		t
	R=100 Ом			E
2	R=100 Ом		2
2	L=10-5 Гн		2
	L=10-5 Гн
				ф	2ф	t
	L=10-5 Гн			E
3	L=10-5 Гн		3
3	R=100 Ом		3
	R=100 Ом
						t

125

Окончание табл. 6 . 2

		R1				E
4		R1	R2		4
4		C1	R2		4
		C1					ф		t
							ф		t
		C1	R2			E/2
5			R2		5
5			ОУ		5		ф	2ф	t
		R1	ОУ				ф	2ф	t
		R1
	R1		R2			E/2
6	R1			C2	6
				C2					t
			ОУ				ф	2ф
			ОУ				ф	2ф
						E
7			R2		7	E / 2
7	R1	С1	ОУ		7
	R1	С1	ОУ				ф	2ф	t
									t

						E
8			R2	C2	8	E / 2
8	R1	С1	ОУ		8
	R1	С1	ОУ				ф	2ф	t
									t

		R2				E
		R1				E
		R1
9				C2	9
	C1		ОУ	C2			ф	2ф	t
	C1						ф	2ф	t
6.4.2. ПРОХОЖДЕНИЕ ИМПУЛЬСНЫХ СИГНАЛОВ ЧЕРЕЗ
ИЗБИРАТЕЛЬНЫЕ ЦЕПИ
Постоянная ЭДС			E = 20		В подключается к входу				контура

(рис. 6.16 и 6.17). Схема контура, его параметры и подлежащая определению реакция контура приведены в табл. 6.3.

Требуется определить соответствующую реакцию на заданное входное воздействие.

126	ГЛАВА 6. ПРОХОЖДЕНИЕ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ

R E

Рис. 6.16

Рис. 6.17

Таблица 6 . 3

Номер

Контур

Реакция

Номер

вари-

подва-

R , Ом

C , Ф

L , Гн

анта

рианта

Рис. 6.16

100

10 –5

10 –3

5 10 –6

5 10 –3

10 –6

10 –4

5 10 –5

5 10 –4

10 –5

10 –2

Рис. 6.17

100

10 –4

10 –3

150

5 10 –5

5 10 –3

200

10 –5

10 –1

250

5 10 –6

0,5 10 –2

300

10 –6

10 –2

6.4.3.ПРОХОЖДЕНИЕ РАДИОСИГНАЛОВ ЧЕРЕЗ ИЗБИРАТЕЛЬНЫЕ ЦЕПИ

На колебательный контур (рис. 6.18) воздействует модулированное колебание, параметры которого указаны в табл. 6.4 и 6.5.

Контур	имеет	следующие параметры:		Q =100 ,		Zp =10 кОм,
ωp = ω0 , R =100 Ом.
				L	C
I(t)	L	ZP C	uвых(t) E(t)		R	uвых(t)
		а			б

Рис. 6.18

127

												Таблица 6 . 4

Номер	Схема			Вид		Входной сигнал
вари-	Схема		модуля-			Входной сигнал
анта				ции
0	Рис. 6.18, а			ЧМ		I (t) = Im sin[ω0t + mx(t)]
1	Рис. 6.18, б			ЧМ		E(t) =Um sin[ω0t + mx(t)]
2	Рис. 6.18, а			ФМ		I (t) = Im sin[ω0t + mx(t)]
3	Рис. 6.18, б			ФМ		E(t) =Um sin[ω0t + mx(t)]
4	Рис. 6.18, а			АМ		I (t) = I			1 + Mx(t)		cosω t
4	Рис. 6.18, а			АМ			m [			]		0
5	Рис. 6.18, б			АМ		E(t) =U			1 + Mx(t)			cosω t
5	Рис. 6.18, б			АМ				m [		]		0
6	Рис. 6.18, а			АМ		I (t) = I			1 + Mx(t)		cosω t
6	Рис. 6.18, а			АМ			m [			]		0
7	Рис. 6.18, б			АМ		E(t) =U			1 + Mx(t)			cosω t
7	Рис. 6.18, б			АМ				m [		]		0
8	Рис. 6.18, а			Режим		I (t) = Imσ(t) cos ω0t
8	Рис. 6.18, а		несущей			I (t) = Imσ(t) cos ω0t
			несущей
9	Рис. 6.18, б			Режим		E(t) =Umσ(t) cos ω0t
9	Рис. 6.18, б		несущей			E(t) =Umσ(t) cos ω0t
			несущей
												Таблица 6 . 5

Номер	Im ,	Um ,		f0 ,	F ,	Вариант							Модули-
Номер	Im ,	Um ,		f0 ,	F ,	0–3				4–7			Модули-
подва-	мА	B		MГц	кГц	0–3				4–7			рующая
рианта													функция
рианта						m , рад				M			функция
						m , рад				M
0	0.10	1.0		1.0	1.0	10.0				0.50			sin Ωt
1	0.9	9.0		1.0	2.0	5.0				0.25			cosΩt
2	0.8	8.0		0.75	3.0	2.5				0.75			sin Ωt
3	0.7	7.0		0.8	4.0	2.0				0.50			cosΩt
4	0.6	6.0		0.5	5.0	1.0				0.75			sin Ωt
5	0.5	5.0		1.2	6.0	2.0				0.50			cosΩt
6	0.4	4.0		0.7	7.0	1.0				0.25			sin Ωt
7	0.3	3.0		1.6	8.0	2.0				0.50			cosΩt
8	0.2	2.0		0.9	9.0	1.0				0.75			sin Ωt
9	2.0	1.0		2.0	10.0	2.0				0.25			cosΩt

Требуется:

а) получить выражение для напряжения на контуре; б) построить временную диаграмму огибающей напряжения на

контуре и временную диаграмму огибающей входного сигнала;

128	ГЛАВА 6. ПРОХОЖДЕНИЕ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ

в) для АМ колебания определить величину демодуляции, рассчитать спектр колебания на контуре и построить спектральные диаграммы амплитуд и фаз.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

При выполнении вариантов 0–3 целесообразно воспользоваться методом “мгновенной” частоты, а при выполнении вариантов 4–9 – спектральным методом или методом комплексной огибающей.

В действительности все не так, как на самом деле.

Станислав Ежи Лец

ГЛАВА 7

ПРОХОЖДЕНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ ЧЕРЕЗ ЛИНЕЙНЫЕ РАДИОЦЕПИ

7.1.ИЗУЧАЕМЫЕ ВОПРОСЫ

Спектральная плотность мощности (СПМ) и корреляционная функция стационарного случайного процесса на выходе линейной цепи. Средняя мощность колебаний на выходе. Корреляция между входным и выходным процессами в установившемся режиме. Воздействие белого шума на линейные цепи. Нормализация случайного процесса в линейной цепи. Дифференцирование и интегрирование случайных процессов. Распределение огибающей гауссова процесса и смеси гармонического сигнала с гауссовым шумом [1,

гл.7, 4.6; 2, гл.10, 7.3; 3, гл.19].

Указания. Вопросы анализа случайных процессов (СП) в линейных цепях подробно рассмотрены в [1, 3,11]. Руководства [5…9] содержат большое количество задач с комментариями и решениями.

Большинство встречающихся на практике задач можно разделить на два класса. К первому относят задачи, связанные с определением динамических характеристик выходного процесса (его автокорреляционной функции и спектральной плотности мощности), а также взаимной корреляции случайных процессов (на входе и выходе цепи, на выходах различных цепей при общем входном воздействии и т. п.). Задачи второго класса посвящаются определению плотностей распределения вероятностей мгновенных значений выходного процесса.

В настоящей главе будут рассмотрены задачи, связанные с анализом случайных процессов на выходах линейных стационарных

130	ГЛАВА 7. ПРОХОЖДЕНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ ЧЕРЕЗ

цепей, когда на входы цепей воздействуют стационарные в широком смысле случайные процессы. При этом обычно предполагается, что переходные процессы в цепи закончились (или, что эквива-

лентно, случайный процесс присутствует на входе цепи с момента времени t = −∞ ).

Задачи, связанные с плотностью распределения вероятностей мгновенных значений СП, будут рассматриваться лишь для частного, хотя и важного, случая гауссова процесса.

7.2.КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Если нестационарность СП X (t) выражается лишь в непостоянстве математического ожидания mx (t) , то можно, имея в виду принцип суперпозиции, анализировать отдельно прохождение через линейную цепь детерминированной функции mx (t) и флюктуационной составляющей случайного процесса. При этом

∞

my (t) = ∫ mx (τ)g(t − τ)dτ,

−∞

где my (t) – математическое ожидание выходного процесса Y (t) ; g(t) – импульсная характеристика цепи.

Если процесс X (t) на входе цепи стационарен в широком смысле с автокорреляционной функцией Kx (τ) , то автокорреляционная функция выходного процесса Y (t)

∞	∞	∞
Ky (τ)= ∫	∫ g (u)g (v)Kx (u −v + τ)dudv = ∫ Kx (t )Kg (τ−t )dt,
−∞	−∞	−∞
	∞
где Kg (t) = ∫ g(τ)g(τ+t)dτ		– автокорреляционная функция им-

−∞

пульсной характеристики цепи.

Взаимная корреляционная функция входного и выходного процессов

∞

Kxy (τ)= ∫ g (t)Kx (τ−t)dt.

−∞

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 3613 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке ТОИИТ

#
24.02.201622.54 Кб29Вопросы для экзамена по ТОИИТ.docx
#
24.02.20169.82 Mб126Задания.pdf
#
24.02.201690.11 Кб24Положение о контрольных работах зо.doc