
- •Литература
- •Перечень компьютерных программ, наглядных и других пособий, методических указаний и материалов и технических средств обучения
- •1.2.Операции над множествами
- •1.3. Булева алгебра множеств
- •1.4. Разбиения и покрытия
- •2. Отношения бинарные и n-арные
- •2.1. Декартово произведение
- •2.2. Бинарные отношения (соответствия)
- •2.3. Операции над бинарными отношениями
- •2.4. Функциональные отношения
- •2.5. Бинарные отношения на множестве
- •2.6. Алгебраические системы
- •3. Основные понятия теории графов
- •3.1. Абстрактный граф
- •3.2. Графическое представление бинарного отношения
- •Множеств а и в
- •3.3. Матричные представления графа
- •3.4. Части графа
- •3.5. Достижимость и связность
- •3.6. Доминирующие множества графа
- •3.7. Независимые множества графа
- •3.8. Раскраска графа
- •3.9.Планарность графов
- •3.10. Инварианты графов
- •4. Булевы функции
- •4.1. Способы задания булевой функции
- •4.2. Элементарные булевы функции и алгебраические формы
- •4.3. Интерпретации булевой алгебры
- •4.4. Нормальные формы булевых функций
- •4.4.1. Дизъюнктивные нормальные формы
- •4.4.2. Конъюнктивные нормальные формы
- •4.5 Полнота и замкнутость системы логических функций
- •4.6. Локальные упрощения днф
- •4.6.1. Удаление избыточных элементарных конъюнкций
- •4.6.2. Удаление избыточных литералов
- •4.7. Графическое представление булева пространства и булевых функций
- •4.7.1. Булев гиперкуб
- •4.7.2. Развертка гиперкуба на плоскости. Карта Карно
- •4.8. Минимизация днф
- •4.8.1. Метод Квайна-МакКласки
- •4.8.2. Метод Блейка-Порецкого
- •4.8.3. Визуально-матричный метод минимизации
- •5. Элементы математической логики
- •5.1 Алгебра высказываний
- •Всякое высказывание логично следует из самого себя.
- •2. Закон противоречия:
- •Если из а следует b, а b ложно, то а тоже ложно.
- •5.2. Логические отношения
- •5.3.Проверка правильности рассуждений
- •5.4. Решение логических задач методом характеристического уравнения
- •5.6. Кванторы
- •5.7 Эквивалентные соотношения. Префиксная нормальная форма
- •6. Основы теории алгоритмов
- •6.1. Интуитивное понятие об алгоритме
- •6.2. Три типа алгоритмических моделей
- •6.3. Кризис теории множеств антиномии. Выводы из антиномий
- •6.4. Машины Тьюринга как модели алгоритмов
- •6.5. Алгоритмы решения некоторых задач теории графов на графах
- •7. Конечный автомат и его описание.
- •7.2. Представления автомата
- •7.3. Связь между моделями Мили и Мура
- •7.4. Автомат с абстрактным состоянием. Булев автомат
- •7.5. Понятие о регулярных выражениях алгебры событий.
- •7.6. Задачи абстрактной теории конечных автоматов
- •8. Комбинаторные задачи и методы комбинаторного поиска
- •8.1. Задачи подсчета числа комбинаторных решений
- •8.2. Особенности оптимизационных комбинаторных задач
- •8.3. Вычислительная сложность
- •8.4. Методы комбинаторного поиска
- •8.5. Задача о кратчайшем покрытии и методы ее решения
- •8.5.1. Постановка задачи
- •8.5.2. Приближенные методы решения задачи
- •8.5.3. Точный метод
- •Вопросы к зачету
- •28. Нормальные формы булевых функций. Дизъюнктивные нормальные формы
- •44. Эквивалентные соотношения. Префиксная нормальная форма
- •Практический раздел Контрольная работа Указания по выбору варианта
- •Контрольное задание №1. Используя диаграммы Эйлера-Венна, решить задачу
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №2. Получить сднф, скнф, используя таблицу истинности. Построить днф, кнф, упростив выражение.
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №3. Упростить схему (рис. 2)
- •Методические указания
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №6. Найти инварианты неориентированного графа, заданного матрицей смежности
- •Методические указания
- •Задачи для самостоятельного решения
3.4. Части графа
Граф Н = (W, F) называется подграфом графа G = (V, E), если W V, F E и обе вершины, инцидентные любому ребру из F, принадлежат W. Подграф Н графа G называется его остовным подграфом, если W = V. Если F является множеством всех ребер графа G, все концы которых содержатся в множестве W, то подграф Н = (W, F) называется подграфом, порожденным множеством W.
Любая последовательность вида v1, e1, v2, e2, … , ek, vk + 1, где v1, v2, … , vk + 1 – вершины некоторого графа, а e1, e2, … , ek – его ребра, причем ei = vivi + 1 (i = 1, 2, … , k), называется маршрутом. Маршрут может быть конечным либо бесконечным. Одно и то же ребро может встречаться в маршруте не один раз. Длиной маршрута называется количество входящих в него ребер, причем каждое ребро считается столько раз, сколько оно встречается в данном маршруте.
Маршрут, все ребра которого различны, называется цепью. Цепь, все вершины которой различны, называется простой цепью. С понятием длины цепи связано понятие расстояния в графе. Под расстоянием между двумя вершинами понимается длина кратчайшей цепи, связывающей данные вершины.
Маршрут v1, e1, v2, e2, … , ek, v1 называется циклическим. Циклическая цепь называется циклом. Простой цикл – это циклическая простая цепь.
Любую цепь и любой цикл графа можно рассматривать как его подграф.
Связный граф называется эйлеровым, если он содержит эйлеров цикл, т.е цикл, проходящий по каждому ребру ровно один раз. Для того чтобы граф был эйлеровым, необходимо и достаточно, чтобы он был связным и каждая его вершина имела четную степень (теорема Эйлера), за исключением, может быть, вершин, из которой цикл исходит и в которую заходит. Если в графе существует цепь, проходящая по каждому ребру один раз, она называется эйлеровой, а граф – полуэйлеровым.
Связный граф называется гамильтоновым, если в нем существует цикл, проходящий по каждой вершине ровно один раз (гамильтонов цикл).
3.5. Достижимость и связность
Граф является связным, если между любыми двумя его вершинами имеется цепь. Связный подграф некоторого графа, не содержащийся ни в каком другом его связном подграфе, называется компонентой связности или просто компонентой данного графа.
В ориентированном графе маршрутом называется последовательность вида v1, а1, v2, а2, … , аk, vk + 1, где для всякой дуги аi вершина vi является началом, а vi + 1 – концом. Вершина v1 является началом маршрута, а вершина vk + 1 – его концом. Маршрут, в котором все вершины, кроме, возможно, начальной и конечной, различны, называется путем. Путь вида v1, а1, v2, а2, … , аk, v1 называется контуром.
Вершина vj в ориентированном графе является достижимой из вершины vj, если в этом графе имеется путь с началом в vi и концом в vj. Ориентированный граф является сильно связным, если любая его вершина достижима из любой вершины.
Матрицы достижимостей и контрдостижимостей.
Если существует путь, идущий от вершины xi к вершине xj, то говорят, что xj достижима из вершины xi. Обозначим через R(xi) множество вершин графа, достижимых из вершины xi . Определим маршрут достижимостей R=(rij) с элементами
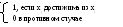
rij =
Очевидно, что все диагональные элементы матрицы R равны 1 (xi достижима из xi ).
Пусть через Г(xi) обозначено множество вершин, которые достижимы из xi с использованием путей длины 1, через Г2(хi) – множество вершин, достижимых из хi c использованием путей длины 2, … , Гp(xi) – множество вершин, достижимых из xi c использованием путей длины Р. Тогда R(xi) можно представить в виде
R(xi) = {xi}Г(xi)Г2(xi)...Гp(xi),
где – операция объединения множеств.
Алгоритм Кристофидеса.
Множество R(xi) получается последовательным выполнением (слева направо) операций объединения в соотношении () до тех пор, пока «текущее» множество не перестает увеличиваться по размеру при очередной операции объединения.
Обозначим через Q(xi) множество вершин, из которых можно достичь вершину xi. Определим маршрут контрдостижимостей Q=(qij) с элементами
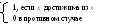
qij =
Пусть через Г-1(xi) обозначено множество вершин, из которых можно достичь вершину xi. С использованием путей длины 1, Г-p(xi) – множество вершин, из которых можно достичь вершину xi с использованием путей длинны р. Тогда Q(xi) можно представить в виде:
Q(xi) = {xi}Г-1(xi)Г-2(xi)...Г-p(xi),
где – операция объединения множеств.
Пример:
Построить матрицы достижимостей и контрдостижимостей для графа G.
x1 x6
x2
x5 x7
x3 x4
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
|
2 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|
3 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
4 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
5 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
6 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
7 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
Матрица смежности C = (Cij)=
Матрица достижимостей R = (rij)
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
|
2 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
|
3 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
4 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
5 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
6 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
|
7 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
Матрица контрдостижимостей Q = (qij)
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
3 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
|
4 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
|
5 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
6 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
7 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
