
- •Литература
- •Перечень компьютерных программ, наглядных и других пособий, методических указаний и материалов и технических средств обучения
- •1.2.Операции над множествами
- •1.3. Булева алгебра множеств
- •1.4. Разбиения и покрытия
- •2. Отношения бинарные и n-арные
- •2.1. Декартово произведение
- •2.2. Бинарные отношения (соответствия)
- •2.3. Операции над бинарными отношениями
- •2.4. Функциональные отношения
- •2.5. Бинарные отношения на множестве
- •2.6. Алгебраические системы
- •3. Основные понятия теории графов
- •3.1. Абстрактный граф
- •3.2. Графическое представление бинарного отношения
- •Множеств а и в
- •3.3. Матричные представления графа
- •3.4. Части графа
- •3.5. Достижимость и связность
- •3.6. Доминирующие множества графа
- •3.7. Независимые множества графа
- •3.8. Раскраска графа
- •3.9.Планарность графов
- •3.10. Инварианты графов
- •4. Булевы функции
- •4.1. Способы задания булевой функции
- •4.2. Элементарные булевы функции и алгебраические формы
- •4.3. Интерпретации булевой алгебры
- •4.4. Нормальные формы булевых функций
- •4.4.1. Дизъюнктивные нормальные формы
- •4.4.2. Конъюнктивные нормальные формы
- •4.5 Полнота и замкнутость системы логических функций
- •4.6. Локальные упрощения днф
- •4.6.1. Удаление избыточных элементарных конъюнкций
- •4.6.2. Удаление избыточных литералов
- •4.7. Графическое представление булева пространства и булевых функций
- •4.7.1. Булев гиперкуб
- •4.7.2. Развертка гиперкуба на плоскости. Карта Карно
- •4.8. Минимизация днф
- •4.8.1. Метод Квайна-МакКласки
- •4.8.2. Метод Блейка-Порецкого
- •4.8.3. Визуально-матричный метод минимизации
- •5. Элементы математической логики
- •5.1 Алгебра высказываний
- •Всякое высказывание логично следует из самого себя.
- •2. Закон противоречия:
- •Если из а следует b, а b ложно, то а тоже ложно.
- •5.2. Логические отношения
- •5.3.Проверка правильности рассуждений
- •5.4. Решение логических задач методом характеристического уравнения
- •5.6. Кванторы
- •5.7 Эквивалентные соотношения. Префиксная нормальная форма
- •6. Основы теории алгоритмов
- •6.1. Интуитивное понятие об алгоритме
- •6.2. Три типа алгоритмических моделей
- •6.3. Кризис теории множеств антиномии. Выводы из антиномий
- •6.4. Машины Тьюринга как модели алгоритмов
- •6.5. Алгоритмы решения некоторых задач теории графов на графах
- •7. Конечный автомат и его описание.
- •7.2. Представления автомата
- •7.3. Связь между моделями Мили и Мура
- •7.4. Автомат с абстрактным состоянием. Булев автомат
- •7.5. Понятие о регулярных выражениях алгебры событий.
- •7.6. Задачи абстрактной теории конечных автоматов
- •8. Комбинаторные задачи и методы комбинаторного поиска
- •8.1. Задачи подсчета числа комбинаторных решений
- •8.2. Особенности оптимизационных комбинаторных задач
- •8.3. Вычислительная сложность
- •8.4. Методы комбинаторного поиска
- •8.5. Задача о кратчайшем покрытии и методы ее решения
- •8.5.1. Постановка задачи
- •8.5.2. Приближенные методы решения задачи
- •8.5.3. Точный метод
- •Вопросы к зачету
- •28. Нормальные формы булевых функций. Дизъюнктивные нормальные формы
- •44. Эквивалентные соотношения. Префиксная нормальная форма
- •Практический раздел Контрольная работа Указания по выбору варианта
- •Контрольное задание №1. Используя диаграммы Эйлера-Венна, решить задачу
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №2. Получить сднф, скнф, используя таблицу истинности. Построить днф, кнф, упростив выражение.
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №3. Упростить схему (рис. 2)
- •Методические указания
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №6. Найти инварианты неориентированного графа, заданного матрицей смежности
- •Методические указания
- •Задачи для самостоятельного решения
4.6.2. Удаление избыточных литералов
Рассмотрим второй вид избыточности в ДНФ, когда D = хk D = k D. Здесь избыточным является литерал х. Правую часть этого равенства можно представить следующим образом:
k D = k(х х) D = хk D хk = D хk.
Отсюда видно, что литерал х в выражении хk D является избыточным, если конъюнкция хk является избыточной в выражении D хk. Следовательно, задача определения избыточности литерала в ДНФ сводится к предыдущей задаче – задаче определения избыточности элементарной конъюнкции.
Удаление литерала из ДНФ в матричном представлении выражается в замене нуля или единицы в троичной матрице на значение «–». На основании предыдущих рассуждений это можно сделать, если вектор, полученный из строки, содержащей данный нуль или единицу, заменой этого значения на противоположное ему значение (т. е. 0 на 1 или 1 на 0), является избыточным для рассматриваемой матрицы.
Таким образом, для того, чтобы решить вопрос о том, можно ли заменить 0 (или 1) в i-й строке и j-м столбце на значение «–», надо построить минор, образованный столбцами, где i-я строка имеет значения «–», и строками, не ортогональными вектору, полученному из i-й строки заменой нуля (или единицы) в j-м столбце на противоположное значение. Если полученный минор оказался вырожденной матрицей, то такая замена возможна.
Рассмотрим матрицу
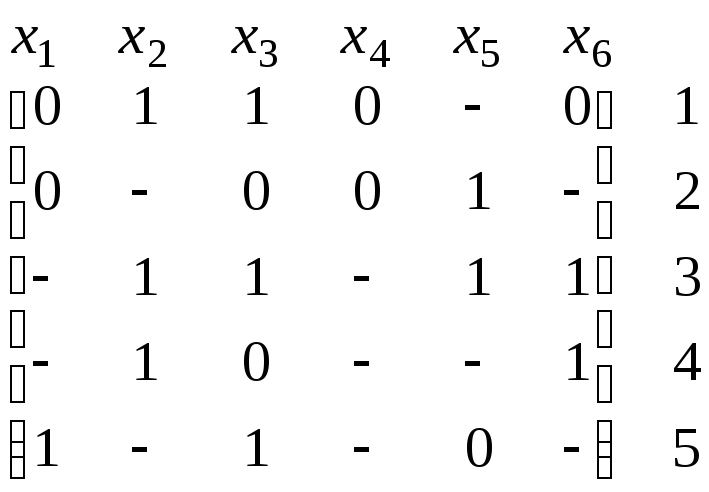 .
.
Чтобы узнать, является ли 0 в строке 1 и столбце х6 избыточным, построим минор, образованный единственным столбцом х5, где строка 1 имеет значение «–», и единственной строкой 3, не ортогональной вектору (0 1 1 0 – 1). Единственный элемент в этом миноре имеет значение 1. Он является невырожденной матрицей. Следовательно, нуль в строке 1 и столбце х6 нельзя заменить на «–».
Рассмотрим теперь единицу в строке 3 и столбце х3. Минор, образованный столбцами х1 и х4 и строками 2 и 4, не ортогональными вектору (– 1 0 – 1 1), имеет вид
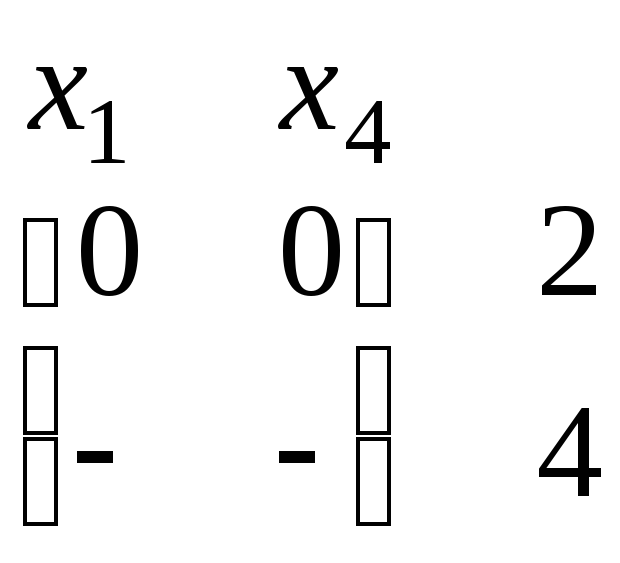 .
.
Вырожденность этого минора говорит о том, данную единицу можно заменить значением «–». Выполнив такую замену, получим матрицу, эквивалентную исходной матрице:
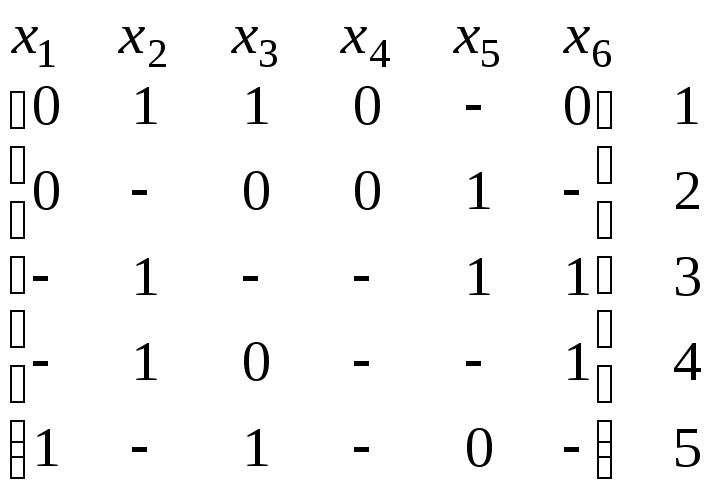 .
.
4.7. Графическое представление булева пространства и булевых функций
4.7.1. Булев гиперкуб
Булево пространство М можно представить в виде графа, вершины которого соответствуют элементам пространства, а ребра представляют отношение соседства между элементами пространства. Два вектора являются соседними, если они отличаются друг от друга значением только одной компоненты. Например, векторы (1 0 0 1) и (1 1 0 1), значения одноименных компонент которых, кроме одной второй компоненты, совпадают, являются соседними. Данный граф, представляющий п-мерное булево пространство, имеет 2п вершин и п2п – 1 ребер. Он называется полным булевым графом, или п-мерным гиперкубом. Рассмотрим построение такого гиперкуба для различных значений размерности пространства.
Одномерный гиперкуб состоит из двух вершин, связанных ребром. Одной из этих вершин приписывается константа 0, другой – константа 1, которые являются кодами данных вершин. Чтобы получить двумерный гиперкуб, надо продублировать одномерный гиперкуб и каждую вершину исходного гиперкуба соединить ребром с ее дублем. Коды вершин построенного двумерного гиперкуба получаются добавлением нулей справа к кодам вершин исходного гиперкуба и единиц – к кодам дублей вершин. Аналогично получаются трехмерный гиперкуб, четырехмерный гиперкуб и т. д.
Сформулируем общее правило увеличения размерности гиперкуба: для перехода от т-мерного гиперкуба к (т + 1)-мерному надо исходный т-мерный гиперкуб продублировать и каждую вершину исходного гиперкуба соединить ребром с ее дублем. В полученном гиперкубе к кодам вершин исходного т-мерного гиперкуба добавляются справа нули, а к кодам их дублей – единицы.
В гиперкубе выделяются гиперграни, которые являются порожденными подграфами, представляющими собой гиперкубы меньшей размерности, чем рассматриваемый гиперкуб. Это может быть отдельное ребро, двумерная грань, трехмерный куб и т. п. Подграф, представляющий гипергрань, порождается множеством вершин, составляющих интервал булева пространства.
