
- •Литература
- •Перечень компьютерных программ, наглядных и других пособий, методических указаний и материалов и технических средств обучения
- •1.2.Операции над множествами
- •1.3. Булева алгебра множеств
- •1.4. Разбиения и покрытия
- •2. Отношения бинарные и n-арные
- •2.1. Декартово произведение
- •2.2. Бинарные отношения (соответствия)
- •2.3. Операции над бинарными отношениями
- •2.4. Функциональные отношения
- •2.5. Бинарные отношения на множестве
- •2.6. Алгебраические системы
- •3. Основные понятия теории графов
- •3.1. Абстрактный граф
- •3.2. Графическое представление бинарного отношения
- •Множеств а и в
- •3.3. Матричные представления графа
- •3.4. Части графа
- •3.5. Достижимость и связность
- •3.6. Доминирующие множества графа
- •3.7. Независимые множества графа
- •3.8. Раскраска графа
- •3.9.Планарность графов
- •3.10. Инварианты графов
- •4. Булевы функции
- •4.1. Способы задания булевой функции
- •4.2. Элементарные булевы функции и алгебраические формы
- •4.3. Интерпретации булевой алгебры
- •4.4. Нормальные формы булевых функций
- •4.4.1. Дизъюнктивные нормальные формы
- •4.4.2. Конъюнктивные нормальные формы
- •4.5 Полнота и замкнутость системы логических функций
- •4.6. Локальные упрощения днф
- •4.6.1. Удаление избыточных элементарных конъюнкций
- •4.6.2. Удаление избыточных литералов
- •4.7. Графическое представление булева пространства и булевых функций
- •4.7.1. Булев гиперкуб
- •4.7.2. Развертка гиперкуба на плоскости. Карта Карно
- •4.8. Минимизация днф
- •4.8.1. Метод Квайна-МакКласки
- •4.8.2. Метод Блейка-Порецкого
- •4.8.3. Визуально-матричный метод минимизации
- •5. Элементы математической логики
- •5.1 Алгебра высказываний
- •Всякое высказывание логично следует из самого себя.
- •2. Закон противоречия:
- •Если из а следует b, а b ложно, то а тоже ложно.
- •5.2. Логические отношения
- •5.3.Проверка правильности рассуждений
- •5.4. Решение логических задач методом характеристического уравнения
- •5.6. Кванторы
- •5.7 Эквивалентные соотношения. Префиксная нормальная форма
- •6. Основы теории алгоритмов
- •6.1. Интуитивное понятие об алгоритме
- •6.2. Три типа алгоритмических моделей
- •6.3. Кризис теории множеств антиномии. Выводы из антиномий
- •6.4. Машины Тьюринга как модели алгоритмов
- •6.5. Алгоритмы решения некоторых задач теории графов на графах
- •7. Конечный автомат и его описание.
- •7.2. Представления автомата
- •7.3. Связь между моделями Мили и Мура
- •7.4. Автомат с абстрактным состоянием. Булев автомат
- •7.5. Понятие о регулярных выражениях алгебры событий.
- •7.6. Задачи абстрактной теории конечных автоматов
- •8. Комбинаторные задачи и методы комбинаторного поиска
- •8.1. Задачи подсчета числа комбинаторных решений
- •8.2. Особенности оптимизационных комбинаторных задач
- •8.3. Вычислительная сложность
- •8.4. Методы комбинаторного поиска
- •8.5. Задача о кратчайшем покрытии и методы ее решения
- •8.5.1. Постановка задачи
- •8.5.2. Приближенные методы решения задачи
- •8.5.3. Точный метод
- •Вопросы к зачету
- •28. Нормальные формы булевых функций. Дизъюнктивные нормальные формы
- •44. Эквивалентные соотношения. Префиксная нормальная форма
- •Практический раздел Контрольная работа Указания по выбору варианта
- •Контрольное задание №1. Используя диаграммы Эйлера-Венна, решить задачу
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №2. Получить сднф, скнф, используя таблицу истинности. Построить днф, кнф, упростив выражение.
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №3. Упростить схему (рис. 2)
- •Методические указания
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №6. Найти инварианты неориентированного графа, заданного матрицей смежности
- •Методические указания
- •Задачи для самостоятельного решения
7.4. Автомат с абстрактным состоянием. Булев автомат
Широко распространенным типом автомата является модель, описываемая одной многозначной внутренней переменной q и многими входными и выходными булевыми переменными х1, х2, … , хп и у1, у2, … , ут. Поведение такого автомата задается системой уравнений
q+ = х1, х2, … , хп; q;
y1 = 1х1, х2, … , хп; q;
y2 = 2х1, х2, … , хп; q;
…
ym = mх1, х2, … , хп; q,
более компактно представляемой в векторной форме
q+ = х, q;
y = х, q.
Функции и отличаются от введенных ранее и только тем, что многозначные входная и выходная переменные оказались замененными на соответствующие булевы векторы, но внутренняя переменная осталась многозначной.
Описанная модель называется автоматом с абстрактным состоянием. Ею удобно пользоваться на начальных этапах логического проектирования дискретных устройств, когда вход и выход устройства описываются как некоторые множества булевых переменных, имеющих конкретную техническую интерпретацию, в то время как множество внутренних переменных представляется пока в простейшей форме, в виде одной многозначной переменной q. Число значений переменной q полагается равным числу различных состояний автомата, при котором он может реализовать заданное функциональное отношение между входом и выходом.
Если заменить внутреннюю переменную qна соответствующий булев векторz (z1, z2, … , zk), то получится система уравнений, в которой все переменные и все функции оказываются булевыми:
z1+ = 1х1, х2, … , хп; z1, z2, … , zk;
z2+ = 2х1, х2, … , хп; z1, z2, … , zk;
…
zk+ = kх1, х2, … , хп; z1, z2, … , zk;
y1 = 1х1, х2, … , хп; z1, z2, … , zk;
y2 = 2х1, х2, … , хп; z1, z2, … , zk;
…
ym = mх1, х2, … , хп; z1, z2, … , zk.
Эта модель называется булевым автоматом. Ее также можно представить в компактной векторной форме:
z+ = х, z;
y = х, z.
Булев автомат в определенном смысле ближе к реальным дискретным устройствам, поскольку его переменные непосредственно реализуются физическими переменными устройства, в частности, на типичных для современной техники элементах с двумя устойчивыми состояниями. Векторы х, у и z показывают структуру абстрактных символов а и b и состояния q. Приведенная выше система функций соответствует структуре, изображенной на рис. 7.2, где КС – комбинационная схема, реализующая приведенную выше систему, а П – блок памяти, осуществляющий задержку на период между соседними моментами времени.
Переменная zi представляет состояние i-го двоичного элемента памяти, а выражение
zi+ = iх1, х2, … , хп; z1, z2, … , zk
надо понимать так, что состояние i-го элемента памяти определяется значениями входных символов и состояниями элементов памяти в предыдущий момент времени.
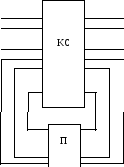
х1 у1
х2 у2
… …
хп ут
z1 z1+
z2 z2+
… …
zk zk+
… …
Рис. 7.2. Структура булева автомата
7.5. Понятие о регулярных выражениях алгебры событий.
Поведение автомата можно было бы описать, поставив каждой входной последовательности однозначно в соответствие выходную последовательность. Но в общем случае это невозможно сделать, из-за бесконечного множества этих входных последовательностей. Выход был найден – использование конечных формул для представления бесконечного множества последовательностей. Эти конечные формулы получили название – «регулярные выражения».
Последовательность входных сигналов будем называть входным словом. Любое множество входных слов назовем событием. Множество входных слов Si, которое вызывает появление на выходе автомата сигнал bi. Назовем событием, представленном в автомате М выходным сигналом bi. Разработана специальная алгебра – алгебра событий. В этой алгебре используются три операции: дизъюнкция, произведение и итерация событий и задаются некоторые законы (правила ТИФ)
Пример:

Элементарное событие – любое множество, состоящее из одного слова или из пустого слова е. Любое событие, представимое конечной формулой алгебры событий, символы элементарных событий, называемое регулярным событием, а сама такая формула – регулярным выражением.
Теорема Клини. Любое регулярное выражение представимо в конечном автомате.
Для задания автомата, имеющего выходной алфавит B=(b1, b2…bi) достаточно разбить множество входных слов на i события S1, S2,… Si, представленных соответственно выходным сигналам b1, b2,.. bi. Поэтому соответственно можно определить реакцию автомата на любое входное слово.
Некоторые примеры представленные регулярным выражением событий во входном алфавите А={a1, a2…. ai}
1)События, содержащие все однобуквенные и только однобуквенные слова алфавита А
S1=a1
![]() a2
a2![]() ….
….
![]() ai
ai
2)События, состоящие из всех двухбуквенных слов алфавита А
S2=(
a1
![]() a2
a2![]() ….
….
![]() ai)(
a1
ai)(
a1
![]() a2
a2![]() ….
….
![]() ai)
ai)
3)События, состоящие из всех слов алфавита А
S3=
{ a1
![]() a2
a2![]() ….
….
![]() ai
}
ai
}
В алфавите (x, y, z) =A регулярное выражение
4)
S4=x{x![]() y
y![]() z}(y
z}(y![]() z)
z)
задает регулярное событие, состоящее из всех слов, которые начинаются буквой x и заканчиваются буквой y или z .
А={x1, x2}
5)описать автомат, выдающий сигнал w1, всякий раз, когда происходит изменение входной буквы с x1на x2, т.е. сигнал w1 должен выдаваться в ответ на любые последовательности, кончающиеся буквами x1 x2
S5={
x1![]() x2}x1x2
x2}x1x2
