
- •Литература
- •Перечень компьютерных программ, наглядных и других пособий, методических указаний и материалов и технических средств обучения
- •1.2.Операции над множествами
- •1.3. Булева алгебра множеств
- •1.4. Разбиения и покрытия
- •2. Отношения бинарные и n-арные
- •2.1. Декартово произведение
- •2.2. Бинарные отношения (соответствия)
- •2.3. Операции над бинарными отношениями
- •2.4. Функциональные отношения
- •2.5. Бинарные отношения на множестве
- •2.6. Алгебраические системы
- •3. Основные понятия теории графов
- •3.1. Абстрактный граф
- •3.2. Графическое представление бинарного отношения
- •Множеств а и в
- •3.3. Матричные представления графа
- •3.4. Части графа
- •3.5. Достижимость и связность
- •3.6. Доминирующие множества графа
- •3.7. Независимые множества графа
- •3.8. Раскраска графа
- •3.9.Планарность графов
- •3.10. Инварианты графов
- •4. Булевы функции
- •4.1. Способы задания булевой функции
- •4.2. Элементарные булевы функции и алгебраические формы
- •4.3. Интерпретации булевой алгебры
- •4.4. Нормальные формы булевых функций
- •4.4.1. Дизъюнктивные нормальные формы
- •4.4.2. Конъюнктивные нормальные формы
- •4.5 Полнота и замкнутость системы логических функций
- •4.6. Локальные упрощения днф
- •4.6.1. Удаление избыточных элементарных конъюнкций
- •4.6.2. Удаление избыточных литералов
- •4.7. Графическое представление булева пространства и булевых функций
- •4.7.1. Булев гиперкуб
- •4.7.2. Развертка гиперкуба на плоскости. Карта Карно
- •4.8. Минимизация днф
- •4.8.1. Метод Квайна-МакКласки
- •4.8.2. Метод Блейка-Порецкого
- •4.8.3. Визуально-матричный метод минимизации
- •5. Элементы математической логики
- •5.1 Алгебра высказываний
- •Всякое высказывание логично следует из самого себя.
- •2. Закон противоречия:
- •Если из а следует b, а b ложно, то а тоже ложно.
- •5.2. Логические отношения
- •5.3.Проверка правильности рассуждений
- •5.4. Решение логических задач методом характеристического уравнения
- •5.6. Кванторы
- •5.7 Эквивалентные соотношения. Префиксная нормальная форма
- •6. Основы теории алгоритмов
- •6.1. Интуитивное понятие об алгоритме
- •6.2. Три типа алгоритмических моделей
- •6.3. Кризис теории множеств антиномии. Выводы из антиномий
- •6.4. Машины Тьюринга как модели алгоритмов
- •6.5. Алгоритмы решения некоторых задач теории графов на графах
- •7. Конечный автомат и его описание.
- •7.2. Представления автомата
- •7.3. Связь между моделями Мили и Мура
- •7.4. Автомат с абстрактным состоянием. Булев автомат
- •7.5. Понятие о регулярных выражениях алгебры событий.
- •7.6. Задачи абстрактной теории конечных автоматов
- •8. Комбинаторные задачи и методы комбинаторного поиска
- •8.1. Задачи подсчета числа комбинаторных решений
- •8.2. Особенности оптимизационных комбинаторных задач
- •8.3. Вычислительная сложность
- •8.4. Методы комбинаторного поиска
- •8.5. Задача о кратчайшем покрытии и методы ее решения
- •8.5.1. Постановка задачи
- •8.5.2. Приближенные методы решения задачи
- •8.5.3. Точный метод
- •Вопросы к зачету
- •28. Нормальные формы булевых функций. Дизъюнктивные нормальные формы
- •44. Эквивалентные соотношения. Префиксная нормальная форма
- •Практический раздел Контрольная работа Указания по выбору варианта
- •Контрольное задание №1. Используя диаграммы Эйлера-Венна, решить задачу
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №2. Получить сднф, скнф, используя таблицу истинности. Построить днф, кнф, упростив выражение.
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №3. Упростить схему (рис. 2)
- •Методические указания
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №6. Найти инварианты неориентированного графа, заданного матрицей смежности
- •Методические указания
- •Задачи для самостоятельного решения
6.5. Алгоритмы решения некоторых задач теории графов на графах
Нахождение наибольшего независимого множества достаточно сложная алгоритмическая задача, поэтому чаще всего ищут близкое к наибольшему независимому множеству и применяют более простые алгоритмы, как, например:
1. В графе выбрать вершину с наименьшей степенью в качестве элемента исходного множества.
2. Удалить выбранную вершину из графа вместе с ее окрестностью (смежные вершины и инцидентные им ребра).
Шаги 1—2 повторять до тех пор, пока множество вершин не станет пустым.
Алгоритм поиска наибольшего паросочетания:
1. Выбираем ребро с наименьшей степенью (число инцидентных вершин) и включаем в искомое паросочетание. Если таковых несколько, выбираем то из них, для которого степень второй граничной вершины наименьшая.
2. Удаляем из графа это ребро и ребра, смежные с ним.
Шаги 1—2 повторять до тех пор, пока множество ребер не станет пустым.
Для решения задачи о нахождении доминирующего множества графа применяется следующий алгоритм:
1. Дополнить матрицу смежности единицами по главной диагонали.
2. Выбрать из матрицы смежности строку с наибольшим числом единиц и ввести ее в искомое покрытие.
3. Вычеркнуть строку из матрицы и столбцы, покрываемые этой строкой.
Повторять шаги 2 и 3 до тех пор, пока в матрице множество столбцов не окажется пустым.
Для решения задачи о наименьшем вершинном покрытии необходимо найти кратчайшее строчное покрытие для матрицы инцидентности по алгоритму:
1. В матрице инцидентности графа отыскивается столбец с наименьшим числом единиц (если таких столбцов несколько, берем самый левый).
2. Среди строк, покрывающих столбец, отыскивается строка с наибольшим числом единиц и включается в искомое покрытие (если таких строк несколько, выбирается самая верхняя).
3. Из матрицы вычеркивается выбранная строка и столбцы, которые она покрывает.
Повторять шаги 1-3 до тех пор, пока в матрице множество столбцов не окажется пустым.
Доминирующее множество ребер, или реберное покрытие - такое множество ребер связного графа, что каждая вершина графа инцидентна хотя бы одному ребру, входящему в доминирующее множество ребер.
Всякое множество одноцветных вершин графа является независимым подмножеством, поэтому задачу о раскраске графа в минимальное количество цветов можно осуществить следующим образом (приближенный алгоритм):
1. Найти все независимые подмножества.
2. В булевой матрице получить кратчайшее вершинное покрытие графа независимыми подмножествами.
7. Конечный автомат и его описание.
7.1. Автомат с памятью
До сих пор рассматривались устройства, не обладающие памятью. Такие устройства в любой момент времени на любую комбинацию входных двоичных сигналов реагируют однозначно, т. е. каждой комбинации двоичных сигналов на входе устройства соответствует определенная комбинация двоичных сигналов на выходе независимо от того, какие сигналы приходили на вход раньше. Отсюда происходят названия «комбинационный автомат» или «комбинационная схема».
Общепринятой
моделью поведения такого устройства
является система булевых функций.
Комбинации двоичных сигналов иногда
удобно обозначать абстрактными символами
или буквами некоторого заданного
алфавита. Пусть имеется входной алфавит
А = {a1, a2, … , a}
и выходной алфавит В = {b1, b2, … , b}.
Тогда общий вид описания поведения
комбинационного автомата можно
представить табл. 7.1, где
![]() В.
Эта таблица является аналогом таблицы
истинности. Она полностью определяет
алгоритм функционирования заданного
устройства.
В.
Эта таблица является аналогом таблицы
истинности. Она полностью определяет
алгоритм функционирования заданного
устройства.
Таблица 7.1
Пример задания комбинационного автомата
-
Вход
Выход
а1
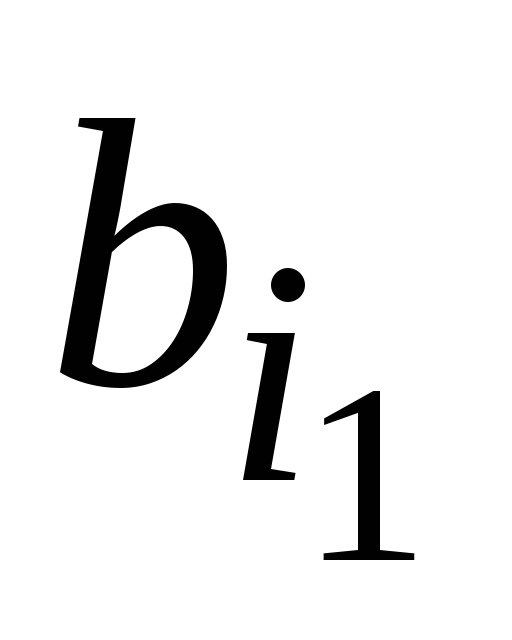
а2
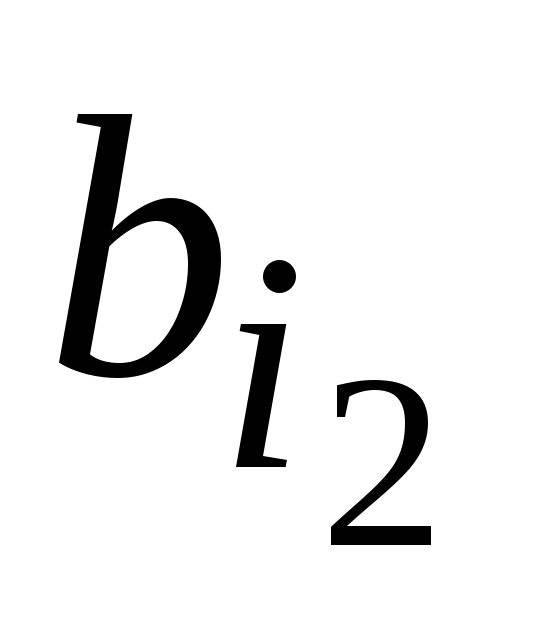
…
…
а
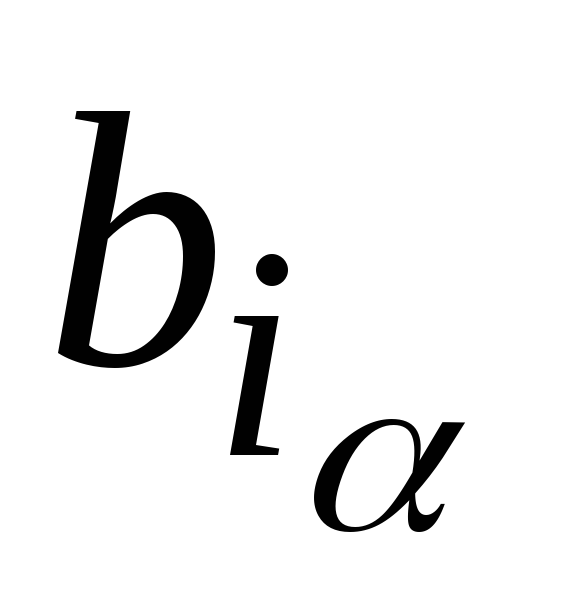
Часто алгоритм функционирования устройства бывает таким, что простым соответствием вида табл. 7.1 его задать невозможно. Для его описания необходимо ввести время, и работа устройства рассматривается во времени. Время носит дискретный характер, т. е. течение времени представляется как последовательность моментов. В любой момент времени устройство принимает сигнал на входе и выдает сигнал на выходе. В различные моменты устройство может реагировать на один и тот же входной сигнал по-разному. Пусть, например, на вход устройства с входным и выходным алфавитами А = {a1, a2, а3, a4} и В = {b1, b2, b3} пришла последовательность сигналов
a1 a1 а3 a2 a2 а4 a3,
а на выходе наблюдается последовательность сигналов
b2 b3 b2 b1 b3 b2 b1.
В первый момент времени устройство на входной сигнал а1 реагировало выходным сигналом b2, а во второй момент на тот же сигнал – сигналом b3. На сигналы а2 и а3 в разные моменты оно реагировало также по-разному, т. е. поведение устройства нельзя описать тем же способом, что использовался для описания поведения комбинационного автомата.
Эта неоднозначность устраняется, если ввести понятие внутреннего состояния или просто состояния. Тогда то, что устройство реагирует на один и тот же сигнал в разные моменты по-разному, можно объяснить так, что оно находится при этом в разных состояниях. Приняв входной сигнал, устройство выдает выходной сигнал и может перейти в другое состояние.
Состояния образуют множество Q {q1, q2, … , q}. Тогда алгоритм функционирования устройства можно представить совокупностью строк вида
(ai, qj) (qs, bt),
где ai А, bt В, qj, qs Q. Устройство, поведение которого можно задать в таком виде, носит название «автомат с памятью» или «последовательностный автомат». Последний термин заключает в себе смысл отображения входной последовательности в другую.
Соответствие (ai, qj) (qs, bt) можно задать таблицей, подобной табл. 7.1, где фактически представлены две функции, определенные на множестве A Q. Областью значений одной функции является множество Q, другой функции – множество В.
Моделью описанного устройства является конечный автомат, представляющий собой совокупность следующих объектов:
А = {a1, a2, … , a} – множество входных символов, или входной алфавит;
В = {b1, b2, … , b} – множество выходных символов, или выходной алфавит;
Q {q1, q2, … , q} – множество состояний, или внутренний алфавит;
: A Q Q – функция переходов;
: A Q В – функция выходов.
Для конечного автомата используется обозначение (A, B, Q, ). Слово «конечный» подчеркивает, что все три множества, входящие в состав данной модели, конечны. В том виде, в каком эта модель здесь представлена, она носит название «автомат Мили». Другой разновидностью данной модели является автомат Мура, отличающийся от автомата Мили только тем, что функция выходов не зависит от входного символа, т. е. представляет собой отображение : Q В.
Значением функции (a, q) является состояние q+, в которое переходит автомат из состояния q, если на вход его подан символ а. Значением функции (a, q) является выходной символ, выдаваемый автоматом в состоянии q при поступлении на его вход символа а, а значением функции (q) автомата Мура – выходной символ b, который выдает автомат, находясь в состоянии q. Если значения функций (a, q) и (a, q) определены для любой пары значений аргументов а и q, а в модели Мура функция (q) определена для всех значений q, то автомат является полностью определенным, или полным автоматом. Иногда приходится иметь дело с не полностью определенным, или частичным автоматом, у которого эти функции могут быть определены не везде.
Конечный автомат является абстрактной математической моделью дискретного устройства. Поведение, описанное данной моделью, может быть по-разному реализовано в дискретном устройстве. При синхронной реализации моменты времени, когда определяется состояние, в которое переходит устройство, а в случае автомата Мили и выходной символ, зафиксированы. Технически это осуществляется введением генератора синхронизирующих сигналов, которые инициируют соответствующие действия. Период следования таких сигналов не должен быть меньше чем время, необходимое для завершения переходных процессов в устройстве. Реализованный таким образом конечный автомат называется синхронным автоматом.
При асинхронной реализации указанные моменты времени не фиксированы. Они связаны с моментами, в которые происходит изменение входного сигнала. Реализованный таким образом автомат называется асинхронным автоматом. Если синхронный автомат различает последовательности разной длины из одинаковых входных символов, т. е. может реагировать на них различными выходными последовательностями, то асинхронный автомат воспринимает последовательность одинаковых входных символов любой длины как один символ. В схеме такого устройства генератор синхронизирующих сигналов отсутствует.
В асинхронном автомате переход из состояния в состояние происходит за некоторый конечный промежуток времени, в течение которого не должен меняться входной сигнал. При действии любого входного сигнала автомат приходит в некоторое устойчивое состояние, из которого он не выходит до конца действия данного сигнала. При этом должно выполняться требование прямого перехода, которое формально выражается следующим образом: если (a, qi) = qj, то (a, qj) = qj. Иногда допускается выполнение следующей цепочки переходов: (a, qi) = qr, (a, qr) = qs, … , (a, qt) = qj, (a, qj) = qj.
