
- •Литература
- •Перечень компьютерных программ, наглядных и других пособий, методических указаний и материалов и технических средств обучения
- •1.2.Операции над множествами
- •1.3. Булева алгебра множеств
- •1.4. Разбиения и покрытия
- •2. Отношения бинарные и n-арные
- •2.1. Декартово произведение
- •2.2. Бинарные отношения (соответствия)
- •2.3. Операции над бинарными отношениями
- •2.4. Функциональные отношения
- •2.5. Бинарные отношения на множестве
- •2.6. Алгебраические системы
- •3. Основные понятия теории графов
- •3.1. Абстрактный граф
- •3.2. Графическое представление бинарного отношения
- •Множеств а и в
- •3.3. Матричные представления графа
- •3.4. Части графа
- •3.5. Достижимость и связность
- •3.6. Доминирующие множества графа
- •3.7. Независимые множества графа
- •3.8. Раскраска графа
- •3.9.Планарность графов
- •3.10. Инварианты графов
- •4. Булевы функции
- •4.1. Способы задания булевой функции
- •4.2. Элементарные булевы функции и алгебраические формы
- •4.3. Интерпретации булевой алгебры
- •4.4. Нормальные формы булевых функций
- •4.4.1. Дизъюнктивные нормальные формы
- •4.4.2. Конъюнктивные нормальные формы
- •4.5 Полнота и замкнутость системы логических функций
- •4.6. Локальные упрощения днф
- •4.6.1. Удаление избыточных элементарных конъюнкций
- •4.6.2. Удаление избыточных литералов
- •4.7. Графическое представление булева пространства и булевых функций
- •4.7.1. Булев гиперкуб
- •4.7.2. Развертка гиперкуба на плоскости. Карта Карно
- •4.8. Минимизация днф
- •4.8.1. Метод Квайна-МакКласки
- •4.8.2. Метод Блейка-Порецкого
- •4.8.3. Визуально-матричный метод минимизации
- •5. Элементы математической логики
- •5.1 Алгебра высказываний
- •Всякое высказывание логично следует из самого себя.
- •2. Закон противоречия:
- •Если из а следует b, а b ложно, то а тоже ложно.
- •5.2. Логические отношения
- •5.3.Проверка правильности рассуждений
- •5.4. Решение логических задач методом характеристического уравнения
- •5.6. Кванторы
- •5.7 Эквивалентные соотношения. Префиксная нормальная форма
- •6. Основы теории алгоритмов
- •6.1. Интуитивное понятие об алгоритме
- •6.2. Три типа алгоритмических моделей
- •6.3. Кризис теории множеств антиномии. Выводы из антиномий
- •6.4. Машины Тьюринга как модели алгоритмов
- •6.5. Алгоритмы решения некоторых задач теории графов на графах
- •7. Конечный автомат и его описание.
- •7.2. Представления автомата
- •7.3. Связь между моделями Мили и Мура
- •7.4. Автомат с абстрактным состоянием. Булев автомат
- •7.5. Понятие о регулярных выражениях алгебры событий.
- •7.6. Задачи абстрактной теории конечных автоматов
- •8. Комбинаторные задачи и методы комбинаторного поиска
- •8.1. Задачи подсчета числа комбинаторных решений
- •8.2. Особенности оптимизационных комбинаторных задач
- •8.3. Вычислительная сложность
- •8.4. Методы комбинаторного поиска
- •8.5. Задача о кратчайшем покрытии и методы ее решения
- •8.5.1. Постановка задачи
- •8.5.2. Приближенные методы решения задачи
- •8.5.3. Точный метод
- •Вопросы к зачету
- •28. Нормальные формы булевых функций. Дизъюнктивные нормальные формы
- •44. Эквивалентные соотношения. Префиксная нормальная форма
- •Практический раздел Контрольная работа Указания по выбору варианта
- •Контрольное задание №1. Используя диаграммы Эйлера-Венна, решить задачу
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №2. Получить сднф, скнф, используя таблицу истинности. Построить днф, кнф, упростив выражение.
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №3. Упростить схему (рис. 2)
- •Методические указания
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №6. Найти инварианты неориентированного графа, заданного матрицей смежности
- •Методические указания
- •Задачи для самостоятельного решения
5.4. Решение логических задач методом характеристического уравнения
Алгоритм решения:
Введение булевых переменных, соответствующих простым высказываниям
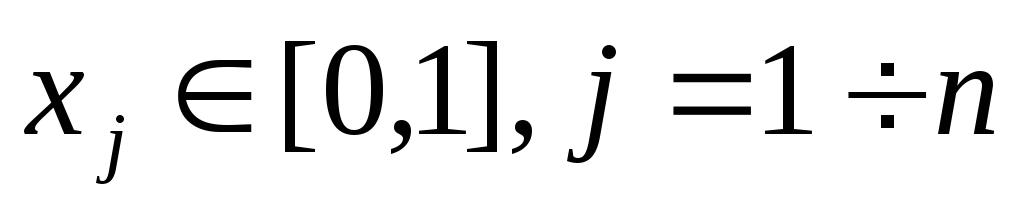
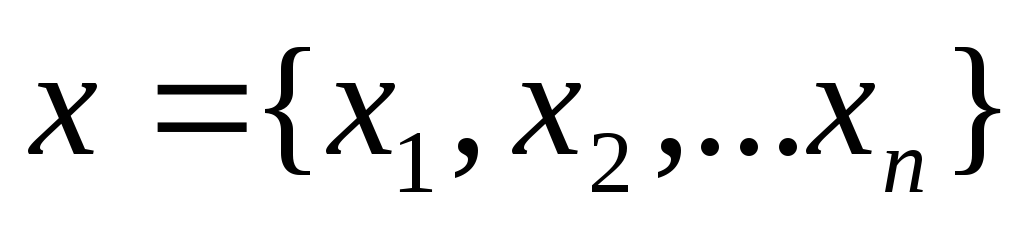
Запись условия задачи в виде логических уравнений
![]() (*)
(*)
где
![]() логическая
функция
логическая
функция
Сведение системы уравнений к характеристическому уравнению
![]() (**)
(**)
множество корней, которого совпадает с множеством корней системы (*)
Приведение левой части характеристического уравнения к ДНФ и решение его:
Приравнивание каждого слагаемого ДНФ (СДНФ), независимо от других, к единице извлечение из уравнения значений переменных. Каждый их набор является решением задачи.
Если после упрощения в ДНФ осталось только одно слагаемое, задача имеет единственное решение. В случае, когда в левой части уравнения все слагаемые уничтожены, задача не имеет решения.
Рассмотрим применение этого алгоритма на примере одной из логических задач.
Задача Р.М. Смаллиана «Принцесс и тигр».
В некотором царстве правил король. Однажды он предложил узнику отгадать, в какой комнате находится принцесса, а в какой тигр. Узнику было объявлено, что в каждой комнате находится либо принцесса, либо тигр, однако может оказаться, что сразу в обеих комнатах будет обнаружено по тигру или по принцессе.
На табличках, прикрепленных к двери каждой из комнат, было написано:
-
1.
2.
В этой комнате находится принцесса, а в другой комнате сидит тигр.

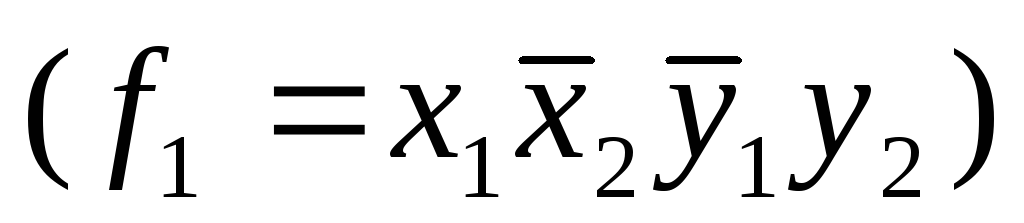
В одной из этих комнат находится принцесса, кроме того, в одной из этих комнат сидит тигр.
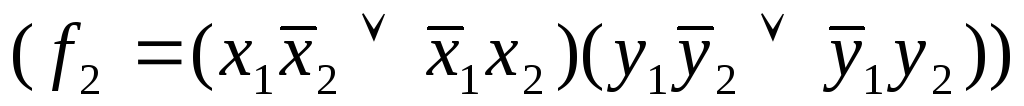
Король сообщил узнику, что на одной из таблиц написана правда, на другой – ложь. Какую дверь надо открыть узнику, если он предпочитает принцессу тигру?
Решение:
Формулируем простые высказывания:
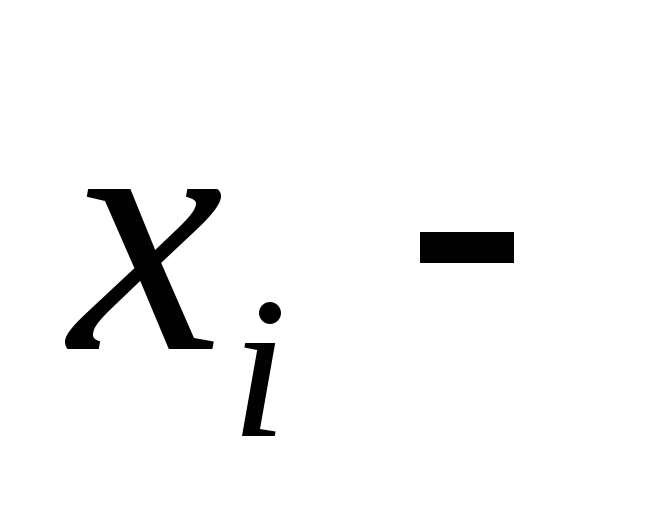 «принцесса
находится в комнате i»:
i=1,2;
«принцесса
находится в комнате i»:
i=1,2; -
«тигр сидит в комнате i»:
i=1,2;
-
«тигр сидит в комнате i»:
i=1,2;
формулируем сложные высказывания, соответствующие условию задачи:
![]()
![]()
![]()
Получаем систему уравнений:
![]()
Составляем характеристическое уравнение:
![]()
Приведение левой части характеристического уравнения к ДНФ. Реализуем с помощью матричного представления логических функции:
И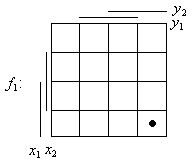
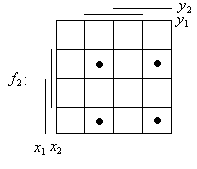
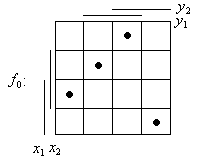
![]()
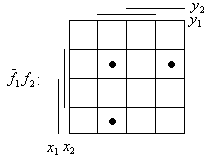
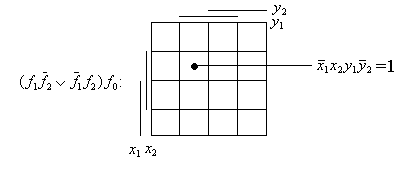 з
последней матрицы видно, что ДНФ содержит
только одно слагаемое.
з
последней матрицы видно, что ДНФ содержит
только одно слагаемое.
Решением
уравнения
![]() является набор 0110, т.е. принцесса находится
в комнате 2, а тигр в комнате 1.
является набор 0110, т.е. принцесса находится
в комнате 2, а тигр в комнате 1.
5.5. Алгебра предикатов
Логика предикатов представляет собой развитие логики высказываний. С помощью формул логики высказываний, например алгебры логики, можно описать и исследовать структуру сложных высказываний, установить их истинность или ложность в зависимости от истинности или ложности входящих в нее простых высказываний. Для описания внутренней логической структуры простых высказываний (т.е. высказываний, не содержащих связок) используется понятие предиката.
Предикат - повествовательное предложение, содержащее предметные переменные, определенные на соответствующих множествах. При замене переменных конкретными значениями (элементами) этих множеств предложение обращается в высказывание, т.е. принимает значение "истинно" или "ложно".
n-местный
предикат - это
функция Р(х1,х2,...,хn)
от n переменных,
принимающих значения из некоторых
заданных предметных областей, так
что х1![]() М1,
х2
М1,
х2![]() М2,...,
хn
М2,...,
хn![]() Мn,
а функция Р
принимает два
логических значения - "истинно"
или "ложно" ({И, Л}, {1, 0}). Таким образом,
предикат Р(х1,х2,...,хn)
является функцией типа Р:
М1×М2×...×Мn
→ В,
где множества
М1,М2,...,Мn
называются
предметными
областями предиката;
х1,х2,...,хn
- предметными
переменными предиката;
В - двоичное
(бинарное) множество {И, Л} или {1,0}.
Мn,
а функция Р
принимает два
логических значения - "истинно"
или "ложно" ({И, Л}, {1, 0}). Таким образом,
предикат Р(х1,х2,...,хn)
является функцией типа Р:
М1×М2×...×Мn
→ В,
где множества
М1,М2,...,Мn
называются
предметными
областями предиката;
х1,х2,...,хn
- предметными
переменными предиката;
В - двоичное
(бинарное) множество {И, Л} или {1,0}.
В качестве примера рассмотрим три высказывания:
А - "Рубль - валюта России";
В - "Доллар - валюта России";
С - "Доллар - валюта США".
Высказывания А и С - истинны, а В - ложно. Если вместо конкретных наименований валюты в выражениях А, В (и, может быть, аналогичных им) подставить предметную переменную х и определить ее на множестве наименований денежных единиц {рубль, доллар, фунт стерлингов,..., марка}, то получим одноместный предикат Р(х) - "х - валюта России".
Если
в выражениях А,
В, С (или
аналогичных им) вместо конкретных
наименований валюты и государства
подставить соответственно переменные
x и
у, где
у
![]() {Россия, США, Англия,...,Германия}, получим
двухместный предикат P(x,
у) – «x - валюта
у». Общим для этих предикатов является
то, что, приписав значения входящим в
них переменным из соответствующих
областей определения, получим
высказывания, обладающие свойством
"истинно" или "ложно".
{Россия, США, Англия,...,Германия}, получим
двухместный предикат P(x,
у) – «x - валюта
у». Общим для этих предикатов является
то, что, приписав значения входящим в
них переменным из соответствующих
областей определения, получим
высказывания, обладающие свойством
"истинно" или "ложно".
С помощью логических связок (и скобок) предикаты могут объединяться в разнообразные логические формулы - предикатные формулы. Исследование предикатных формул и способов установления их истинности является основным предметом логики предикатов. Логика предикатов вместе с входящей в нее логикой высказываний является основой логического языка математики. С ее помощью удается формализовать и точно исследовать основные методы построения математических теорий. Логика предикатов является важным средством построения развитых логических языков и формальных систем (формальных теорий).
Логика предикатов, как и логика высказываний, может быть построена в виде алгебры логики предикатов и исчисления предикатов. Здесь, как и в случае логики высказываний, для знакомства с основными понятиями логики предикатов воспользуемся языком алгебры, а не исчислений.
Соответствия между предикатами, отношениями и функциями:
1.
Для любых М и
n существует
взаимно однозначное соответствие между
n-местными
отношениями R![]() Мn
и n-местными
предикатами Р(х1,х2,...,хn),
Р: Мn
→ В:
Мn
и n-местными
предикатами Р(х1,х2,...,хn),
Р: Мn
→ В:
• каждому
n-местному
отношению R
соответствует
предикат Р(х1,х2,...,хn)
такой, что Р(a1,a2,...,an)
= 1, если и только если (a1,a2,...,an)
![]() R;
R;
• всякий
предикат Р(х1,х2,...,хn)
определяет отношение R
такое, что
(a1,a2,...,an)
![]() R, если
и только если Р(a1,a2,...,an)
= 1.
R, если
и только если Р(a1,a2,...,an)
= 1.
При этом R задает область истинности предиката Р.
2. Всякой функции f(х1,х2,...,хn), f: Мn → М, соответствует предикат Р(х1,х2,...,хn,хn+1), P: Mn+l →B, такой, что Р(a1,a2,...,an,an+1) = 1, если и только если f(a1,a2,..., an) = an+1
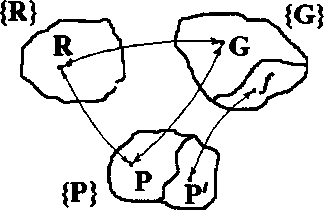
Рис.
5.1
![]() an+1
Р`(a1,a2,...,an,a`n+1)=0.
(5.1)
an+1
Р`(a1,a2,...,an,a`n+1)=0.
(5.1)
Аналогичное
соответствие (взаимно однозначное)
имеется между подмножеством отношений
{R'}![]() {R}
и множеством
функций {f}.
Для этого класса отношений выполняется
аналогичное условие:
{R}
и множеством
функций {f}.
Для этого класса отношений выполняется
аналогичное условие:
если
(a1,a2,...,an,an+1)![]() R',
то для любого
a`n+1
R',
то для любого
a`n+1![]() an+1
(a1,a2,...,an,an+1)
an+1
(a1,a2,...,an,an+1)![]() R'.
(5.2)
R'.
(5.2)
Выражение Р(a1,a2,...,an) будем понимать как высказывание «Р(a1,a2,...,an) =1» или «Р(a1,a2,...,an) истинно», а выражение Р(х1,х2,...,хn) - как переменное высказывание, истинность которого определяется подстановкой элементов множества М вместо переменных х1,х2,...,хn. При этом будем также называть Р(х1,х2,...,хn) логической (двоичной) переменной, в отличие от х1,х2,...,хn - предметных (нелогических) переменных.
Из предикатов как высказываний можно образовывать составные высказывания - формулы логики предикатов.
