
- •Литература
- •Перечень компьютерных программ, наглядных и других пособий, методических указаний и материалов и технических средств обучения
- •1.2.Операции над множествами
- •1.3. Булева алгебра множеств
- •1.4. Разбиения и покрытия
- •2. Отношения бинарные и n-арные
- •2.1. Декартово произведение
- •2.2. Бинарные отношения (соответствия)
- •2.3. Операции над бинарными отношениями
- •2.4. Функциональные отношения
- •2.5. Бинарные отношения на множестве
- •2.6. Алгебраические системы
- •3. Основные понятия теории графов
- •3.1. Абстрактный граф
- •3.2. Графическое представление бинарного отношения
- •Множеств а и в
- •3.3. Матричные представления графа
- •3.4. Части графа
- •3.5. Достижимость и связность
- •3.6. Доминирующие множества графа
- •3.7. Независимые множества графа
- •3.8. Раскраска графа
- •3.9.Планарность графов
- •3.10. Инварианты графов
- •4. Булевы функции
- •4.1. Способы задания булевой функции
- •4.2. Элементарные булевы функции и алгебраические формы
- •4.3. Интерпретации булевой алгебры
- •4.4. Нормальные формы булевых функций
- •4.4.1. Дизъюнктивные нормальные формы
- •4.4.2. Конъюнктивные нормальные формы
- •4.5 Полнота и замкнутость системы логических функций
- •4.6. Локальные упрощения днф
- •4.6.1. Удаление избыточных элементарных конъюнкций
- •4.6.2. Удаление избыточных литералов
- •4.7. Графическое представление булева пространства и булевых функций
- •4.7.1. Булев гиперкуб
- •4.7.2. Развертка гиперкуба на плоскости. Карта Карно
- •4.8. Минимизация днф
- •4.8.1. Метод Квайна-МакКласки
- •4.8.2. Метод Блейка-Порецкого
- •4.8.3. Визуально-матричный метод минимизации
- •5. Элементы математической логики
- •5.1 Алгебра высказываний
- •Всякое высказывание логично следует из самого себя.
- •2. Закон противоречия:
- •Если из а следует b, а b ложно, то а тоже ложно.
- •5.2. Логические отношения
- •5.3.Проверка правильности рассуждений
- •5.4. Решение логических задач методом характеристического уравнения
- •5.6. Кванторы
- •5.7 Эквивалентные соотношения. Префиксная нормальная форма
- •6. Основы теории алгоритмов
- •6.1. Интуитивное понятие об алгоритме
- •6.2. Три типа алгоритмических моделей
- •6.3. Кризис теории множеств антиномии. Выводы из антиномий
- •6.4. Машины Тьюринга как модели алгоритмов
- •6.5. Алгоритмы решения некоторых задач теории графов на графах
- •7. Конечный автомат и его описание.
- •7.2. Представления автомата
- •7.3. Связь между моделями Мили и Мура
- •7.4. Автомат с абстрактным состоянием. Булев автомат
- •7.5. Понятие о регулярных выражениях алгебры событий.
- •7.6. Задачи абстрактной теории конечных автоматов
- •8. Комбинаторные задачи и методы комбинаторного поиска
- •8.1. Задачи подсчета числа комбинаторных решений
- •8.2. Особенности оптимизационных комбинаторных задач
- •8.3. Вычислительная сложность
- •8.4. Методы комбинаторного поиска
- •8.5. Задача о кратчайшем покрытии и методы ее решения
- •8.5.1. Постановка задачи
- •8.5.2. Приближенные методы решения задачи
- •8.5.3. Точный метод
- •Вопросы к зачету
- •28. Нормальные формы булевых функций. Дизъюнктивные нормальные формы
- •44. Эквивалентные соотношения. Префиксная нормальная форма
- •Практический раздел Контрольная работа Указания по выбору варианта
- •Контрольное задание №1. Используя диаграммы Эйлера-Венна, решить задачу
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №2. Получить сднф, скнф, используя таблицу истинности. Построить днф, кнф, упростив выражение.
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №3. Упростить схему (рис. 2)
- •Методические указания
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №6. Найти инварианты неориентированного графа, заданного матрицей смежности
- •Методические указания
- •Задачи для самостоятельного решения
3.9.Планарность графов
Плоский граф – граф, который укладывается на плоскости так, что никакие два его ребра не пересекаются нигде, кроме как в инцидентной им обоим вершине. Граф, изоморфный плоскому, называется планарным. Любой граф, содержащий в качестве подграфа непланарный граф, является непланарным.
Количество граней можно найти для плоского связного графа. Грань – область плоскости, ограниченная ребрами и не содержащая внутри себя ни вершин, ни ребер. При подсчете числа граней плоского графа учитывается и плоская грань.
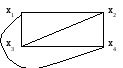
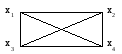
Рис. 3.8. Планарные графы
На рис. 3.8. оба графа планарны, но только второй из них плоский.
Теорема Эйлера о плоском графе. Для любой геометрической реализации плоского связного графа G=(X,E) верно: n-r+f=2, где n=|X|, r=|E|, f - число граней.
Из данной формулы вытекает ряд следствий.
Следствие 1. Если G – связный планарный граф и n≥3, то r≤3n-6.
Доказательство. Пусть G – плоский граф и для него справедлива формула Эйлера. Поскольку каждая грань может быть ограничена по крайней мере тремя ребрами, а каждое ребро соответствует двум граням, то 2r≥3f, следовательно, 3(2-n+r)≤2r или r≤3n-6.
Следствие 2. Графы К5 и К3,3 непланарны.
Доказательство. Пусть К5 планарен. Тогда неравенство r≤3n-6 проводит к противоречию: 10≤9. Следовательно, К5 непланарен.
Пусть К3,3 планарен. Поскольку в двудольном графе нет циклов нечетной длины, то любая его грань ограничена по крайней мере 4 ребрами, т.е. имеет место неравенство 2r≥4f. Подставляя в это неравенство значение f из формулы Эйлера, приходим к противоречию: 20≤18. Следовательно, К3,3 непланарен.
Следствие 3. Для плоского несвязного графа с n вершинами, r ребрами и k компонентами связности имеет место соотношение n-r+f=k+1.
Следствие 4. Сформулируем критерий планарности графа: граф планарен тогда и только тогда, когда он не содержит подграфов, стягиваемых к графам К5 и К3,3. В любом простом планарном графе существует вершина, степень которой не больше пяти.
Назовем толщиной графа t(G) наименьшее число планарных графов, наложение которых дает граф G. Толщина графа является мерой его непланарности, в частности, толщина графов К5 и К3,3 равна 2, а толщина планарного графа равна 1.
Используя формулу Эйлера, нетрудно получить нижнюю оценку для толщины графа G с n≥3:
t(G)≥[r/(3n-6)], t(G)≥{(r+3n-7)/(3n-6)},
где символы [u] и {u} обозначают наибольшее целое число, не превосходящее u, и наименьшее целлон число, которое не меньше u.
3.10. Инварианты графов
Два графа называются изоморфными тогда и только тогда, когда имеется взаимно однозначное соответствие между их вершинами и ребрами при сохранении отношения инцидентности.
Инварианты графа – характеристики графа, которые не меняются при изоморфных преобразованиях графа.
Существуют следующие инварианты графов
Количество вершин n.
Количество ребер r.
Количество граней f.
Число связности k.
Толщина графа t(G).
Плотность графа q(G).
Число независимости
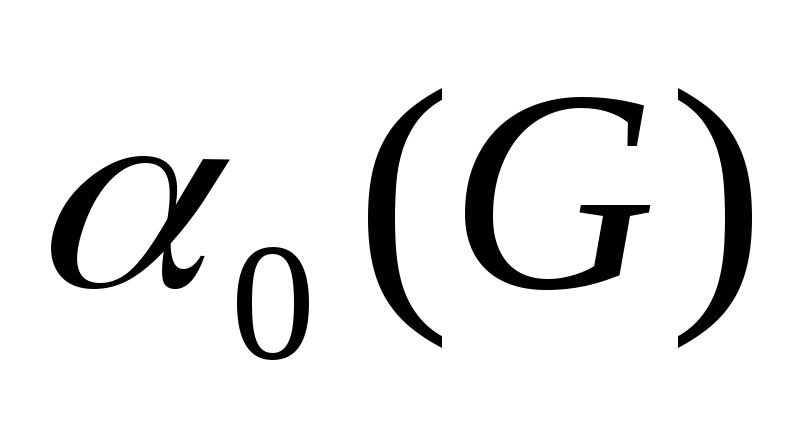
Число вершинного покрытия
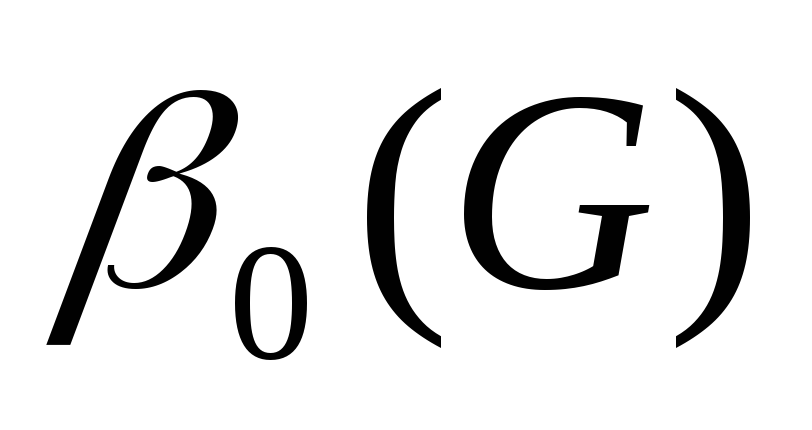
Число паросочетания
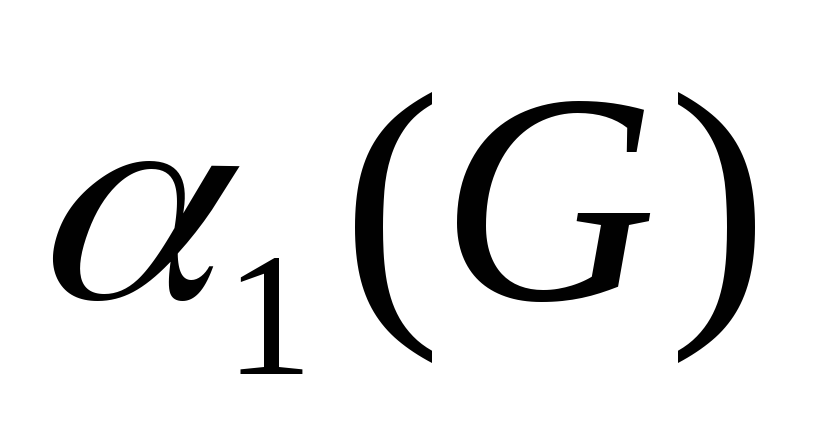 .
.Число реберного покрытия
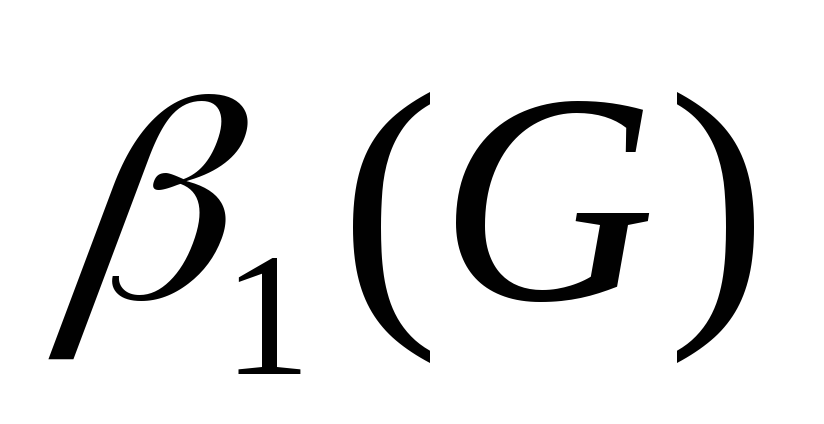 .
.Число доминирования
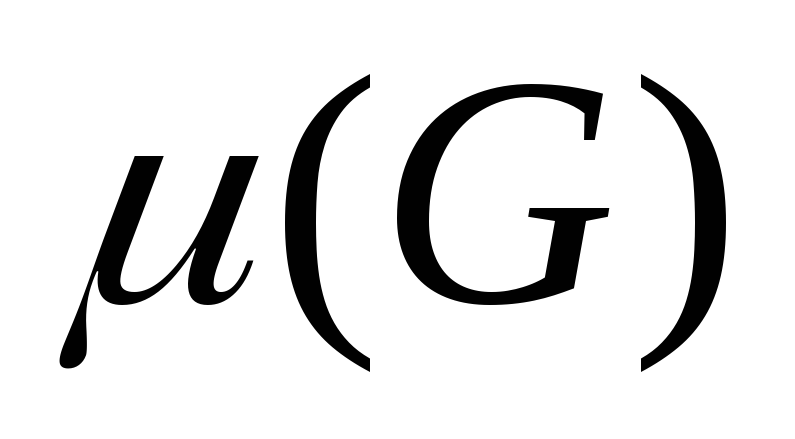
Хроматическое число
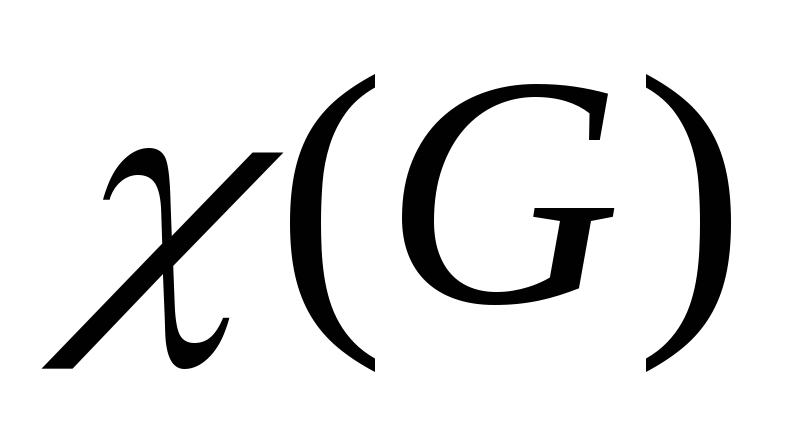
Реберно-хроматическое число
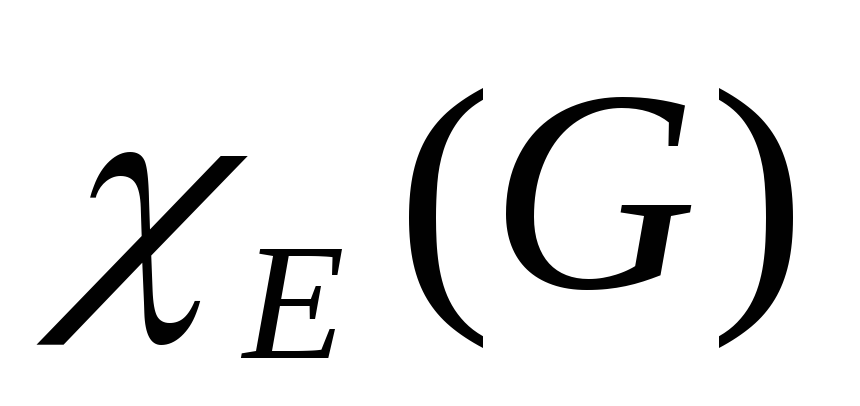
Коцикломатическое число
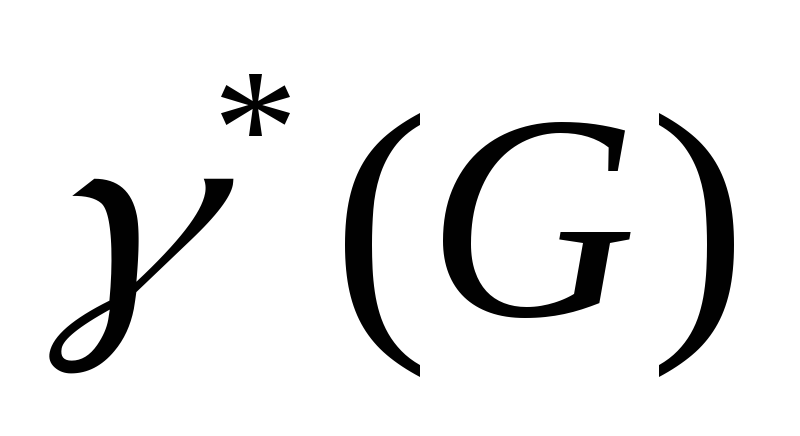
Цикломатическое число
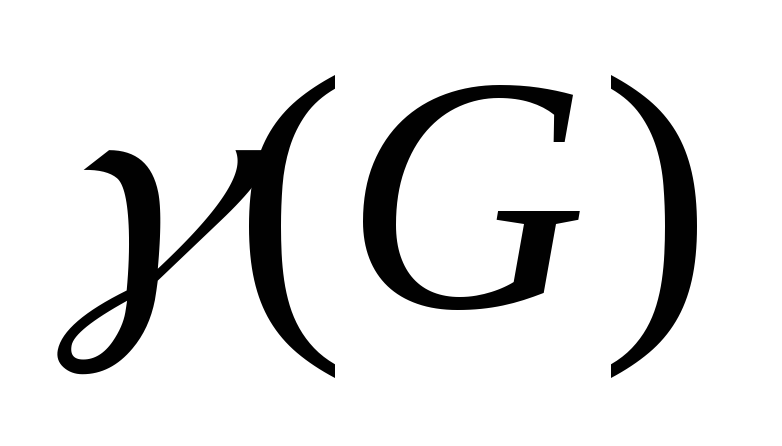
Любой граф можно разбить на подграфы, каждый из которых окажется связным. Минимальное число таких связных компонент называется числом связности графа.
Клика – полный подграф графа G. Количество вершин максимальной клики графа называется плотностью графа.
Независимое множество вершин - множество вершин графа, никакие две вершины которого не инцидентны.
Максимальное независимое множество вершин - независимое множество вершин, которое не содержится ни в каком другом независимом множестве вершин.
Наибольшее независимое множество вершин - независимое множество вершин максимальной мощности.
Мощность наибольшего независимого множества вершин называется числом независимости графа (а также неплотностью, числом внутренней устойчивости или числом вершинной упаковки графа).
Независимое множество ребер, или паросочетание - множество ребер графа, никакие два ребра которого не инцидентны.
Мощность наибольшего паросочетания называется числом паросочетания графа.
Алгоритм поиска наибольшего паросочетания:
1. Выбираем ребро с наименьшей степенью (число инцидентных вершин) и включаем в искомое паросочетание. Если таковых несколько, выбираем то из них, для которого степень второй граничной вершины наименьшая.
2. Удаляем из графа это ребро и ребра, смежные с ним.
Шаги 1—2 повторять до тех пор, пока множество ребер не станет пустым.
Доминирующее множество вершин - такое множество вершин графа, что каждая вершина графа либо принадлежит доминирующему множеству вершин, либо инцидентна некоторой вершине из него. Мощность наименьшего доминирующего множества называется числом доминирования графа.
Для решения задачи о нахождении числа доминирования графа применяется следующий алгоритм:
1. Дополнить матрицу смежности единицами по главной диагонали.
2. Выбрать из матрицы смежности строку с наибольшим числом единиц и ввести ее в искомое покрытие.
3. Вычеркнуть строку из матрицы и столбцы, покрываемые этой строкой.
Повторять шаги 2 и 3 до тех пор, пока в матрице множество столбцов не окажется пустым.
Вершинное покрытие - такое множество вершин графа, что каждое ребро графа инцидентно хотя бы одной вершине, принадлежащей доминирующему множеству вершин.
Мощность наименьшего вершинного покрытия называется числом вершинного покрытия графа.
Для решения задачи о наименьшем вершинном покрытии необходимо найти кратчайшее строчное покрытие для матрицы инцидентности по алгоритму:
1. В матрице инцидентности графа отыскивается столбец с наименьшим числом единиц (если таких столбцов несколько, берем самый левый).
2. Среди строк, покрывающих столбец, отыскивается строка с наибольшим числом единиц и включается в искомое покрытие (если таких строк несколько, выбирается самая верхняя).
3. Из матрицы вычеркивается выбранная строка и столбцы, которые она покрывает.
Повторять шаги 1-3 до тех пор, пока в матрице множество столбцов не окажется пустым.
Доминирующее множество ребер, или реберное покрытие - такое множество ребер связного графа, что каждая вершина графа инцидентна хотя бы одному ребру, входящему в доминирующее множество ребер.
Мощность наименьшего доминирующего множества ребер называется числом реберного покрытия графа.
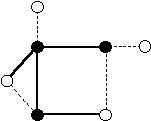
Рис. 3.9
На рис. 3.9 обозначены реберное покрытие графа (пунктиром), максимальное независимое множество вершин (белые вершины) и вершинное покрытие (черные вершины).
Между этими инвариантами существует связь, устанавливаемая следующими леммами.
Лемма
1. Для
любого графа G=(X,E)
сумма числа
вершинного покрытия и числа независимости
постоянна и равна количеству вершин:
![]() +
+![]() =|Х(G)|.
=|Х(G)|.
Лемма
2. Если граф
G=(X,E)
не имеет изолированных вершин, то сумма
его числа паросочетания и числа реберного
покрытия постоянна и равна количеству
вершин:
![]() +
+![]() =|Х(G)|.
=|Х(G)|.
Раскраска вершин графов – разбиение множества вершин графа на подмножества таким образом, чтобы внутри каждого подмножества никакие две вершины не были смежными. Минимальное число красок при решении задачи называется хроматическим числом графа — (G).
Всякое множество одноцветных вершин графа является независимым подмножеством, поэтому раскраску графа в минимальное количество цветов можно осуществить следующим образом:
1. Найти все независимые подмножества.
2. В булевой матрице получить кратчайшее вершинное покрытие графа независимыми подмножествами.
Раскраска ребер – разбиение множества ребер на подмножества таким образом, чтобы внутри каждого подмножества никакие два ребра не были смежными. Минимальное число красок при раскраске ребер называется реберно–хроматическим числом графа — Е(G). Если (х) – максимальная степень вершины графа, то Е(G) +1.
Деревом в неориентированном графе называют связный граф, не имеющий циклов. Если все вершины цикла принадлежат дереву, оно называется покрывающим (остовным). Рёбра графа, принадлежащие покрывающему дереву, называются ветвями, все остальные рёбра графа называются хордами.
Цикломатическое число – число рёбер, удаление которых приводит к покрывающему дереву (число хорд в графе) (G) = r–n+1.
Коцикломатическое число – число рёбер в остовном дереве *(G) = n–1.
