
- •Литература
- •Перечень компьютерных программ, наглядных и других пособий, методических указаний и материалов и технических средств обучения
- •1.2.Операции над множествами
- •1.3. Булева алгебра множеств
- •1.4. Разбиения и покрытия
- •2. Отношения бинарные и n-арные
- •2.1. Декартово произведение
- •2.2. Бинарные отношения (соответствия)
- •2.3. Операции над бинарными отношениями
- •2.4. Функциональные отношения
- •2.5. Бинарные отношения на множестве
- •2.6. Алгебраические системы
- •3. Основные понятия теории графов
- •3.1. Абстрактный граф
- •3.2. Графическое представление бинарного отношения
- •Множеств а и в
- •3.3. Матричные представления графа
- •3.4. Части графа
- •3.5. Достижимость и связность
- •3.6. Доминирующие множества графа
- •3.7. Независимые множества графа
- •3.8. Раскраска графа
- •3.9.Планарность графов
- •3.10. Инварианты графов
- •4. Булевы функции
- •4.1. Способы задания булевой функции
- •4.2. Элементарные булевы функции и алгебраические формы
- •4.3. Интерпретации булевой алгебры
- •4.4. Нормальные формы булевых функций
- •4.4.1. Дизъюнктивные нормальные формы
- •4.4.2. Конъюнктивные нормальные формы
- •4.5 Полнота и замкнутость системы логических функций
- •4.6. Локальные упрощения днф
- •4.6.1. Удаление избыточных элементарных конъюнкций
- •4.6.2. Удаление избыточных литералов
- •4.7. Графическое представление булева пространства и булевых функций
- •4.7.1. Булев гиперкуб
- •4.7.2. Развертка гиперкуба на плоскости. Карта Карно
- •4.8. Минимизация днф
- •4.8.1. Метод Квайна-МакКласки
- •4.8.2. Метод Блейка-Порецкого
- •4.8.3. Визуально-матричный метод минимизации
- •5. Элементы математической логики
- •5.1 Алгебра высказываний
- •Всякое высказывание логично следует из самого себя.
- •2. Закон противоречия:
- •Если из а следует b, а b ложно, то а тоже ложно.
- •5.2. Логические отношения
- •5.3.Проверка правильности рассуждений
- •5.4. Решение логических задач методом характеристического уравнения
- •5.6. Кванторы
- •5.7 Эквивалентные соотношения. Префиксная нормальная форма
- •6. Основы теории алгоритмов
- •6.1. Интуитивное понятие об алгоритме
- •6.2. Три типа алгоритмических моделей
- •6.3. Кризис теории множеств антиномии. Выводы из антиномий
- •6.4. Машины Тьюринга как модели алгоритмов
- •6.5. Алгоритмы решения некоторых задач теории графов на графах
- •7. Конечный автомат и его описание.
- •7.2. Представления автомата
- •7.3. Связь между моделями Мили и Мура
- •7.4. Автомат с абстрактным состоянием. Булев автомат
- •7.5. Понятие о регулярных выражениях алгебры событий.
- •7.6. Задачи абстрактной теории конечных автоматов
- •8. Комбинаторные задачи и методы комбинаторного поиска
- •8.1. Задачи подсчета числа комбинаторных решений
- •8.2. Особенности оптимизационных комбинаторных задач
- •8.3. Вычислительная сложность
- •8.4. Методы комбинаторного поиска
- •8.5. Задача о кратчайшем покрытии и методы ее решения
- •8.5.1. Постановка задачи
- •8.5.2. Приближенные методы решения задачи
- •8.5.3. Точный метод
- •Вопросы к зачету
- •28. Нормальные формы булевых функций. Дизъюнктивные нормальные формы
- •44. Эквивалентные соотношения. Префиксная нормальная форма
- •Практический раздел Контрольная работа Указания по выбору варианта
- •Контрольное задание №1. Используя диаграммы Эйлера-Венна, решить задачу
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №2. Получить сднф, скнф, используя таблицу истинности. Построить днф, кнф, упростив выражение.
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №3. Упростить схему (рис. 2)
- •Методические указания
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №6. Найти инварианты неориентированного графа, заданного матрицей смежности
- •Методические указания
- •Задачи для самостоятельного решения
1.2.Операции над множествами
Самого по себе понятия множества еще недостаточно – необходимо определить способы конструирования новых множеств из уже имеющихся, т.е. определить операции над множествами.
Объединением А
 В
двух множеств А и В
является
множество М,
состоящее из элементов, принадлежащих
хотя бы к одному из множеств А
и В,
т.е.
В
двух множеств А и В
является
множество М,
состоящее из элементов, принадлежащих
хотя бы к одному из множеств А
и В,
т.е.
М=
А![]() В
={m
В
={m![]() m
m![]() А
или m
А
или m![]() В
}.
В
}.
Пересечением А
 В
двух множеств А
и В
является множество М,
состоящее из элементов, принадлежащих
как множеству А,
так и множеству В,
т.е.
В
двух множеств А
и В
является множество М,
состоящее из элементов, принадлежащих
как множеству А,
так и множеству В,
т.е.
М=
А![]() В
={m
В
={m![]() m
m![]() А
и m
А
и m![]() В
}.
В
}.
3. Разностью А \ В множеств А и В является множество М, состоящее из элементов, принадлежащих множеству А и не принадлежащих множеству В, т.е.
М=
А \ В
={m![]() m
m![]() А
и m
А
и m
![]() В
}
В
}
4. Симметрической разностью АВ (А + В) множеств А и В является множество М, содержащее все элементы из А, не принадлежащие В, а также все элементы из В, не принадлежащие А, т.е.
М=
АВ
={m![]() m
m![]() А
и m
А
и m
![]() В
}или ={m
В
}или ={m![]() m
m![]() А
и m
А
и m
![]() В
}
В
}
5. Дополнением![]() ( до
( до![]() .)
множестваМ
является
множество, состоящее из элементов
универсального множества
.)
множестваМ
является
множество, состоящее из элементов
универсального множества![]() ,
не принадлежащих М , т.е.
,
не принадлежащих М , т.е.
![]()
![]() =
{m
=
{m![]() m
m![]()
![]() иm
иm
![]() М
}
М
}
Операцию дополнения
обозначают символом
![]()
![]() .
.
На основе введенных выше операций строятся теоретико-множественные формулы.
а) Любой символ, обозначающий множество, есть формула;
б)
Если А
и В
-
формулы, то А![]() В,
А
В,
А![]() В,
А \ В,
А∆В
(А+В)
– также есть
формулы.
В,
А \ В,
А∆В
(А+В)
– также есть
формулы.
Операции объединения, пересечения и дополнения называются булевыми. Бинарные операции объединения, пересечения, разности и унарная операция дополнения проиллюстрированы на диаграммах Венна (рис.1.1). Результирующее множество элементов, соответствующее каждой из этих операций, изображено заштрихованной областью.
Р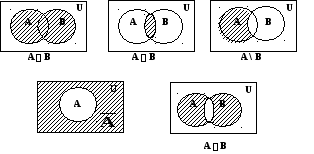 ис.1.1.
Операции над множествами: а) объединение;
б) пересечение; в) разность; г) дополнение;
д) симметрическая разность.
ис.1.1.
Операции над множествами: а) объединение;
б) пересечение; в) разность; г) дополнение;
д) симметрическая разность.
Операции
пересечения и объединения допускают
следующие обобщения. Пусть I– некоторое
множество, элементы которого используются
как индексы, и пусть для любого i![]() I множество Аi
известно. Тогда
I множество Аi
известно. Тогда
![]() Аi
=
{х
Аi
=
{х![]()
![]() i
i![]() I х
I х
![]() Аi
},
Аi
},
![]() Аi
=
{х
Аi
=
{х![]()
![]() i
i![]() I х
I х
![]() Аi
}.
Аi
}.
1.3. Булева алгебра множеств
Абстрактная алгебраическая система, состоящая из множества подмножеств некоторого универсального множества с введенными выше операциями дополнения, пересечения и объединения, составляют булеву алгебру множеств. Перечислим основные законы этой алгебры, используя общепринятое правило, что если в формуле отсутствуют скобки, устанавливающие порядок выполнения операций, то сначала выполняется дополнение, потом пересечение и затем объединение. Для повышения наглядности формулы знак пересечения множеств, подобно знаку арифметического умножения, будем опускать.
Коммутативность:
А В В А; А В В А.
Ассоциативность:
А (В С) (А В) С; А (В C) (А В) С.
Дистрибутивность:
А (В С) А В А С; А В С (А В) (А С).
Идемпотентность:
А А А; А А А.
Законы де Моргана:
![]() =АВ;
=АВ; ![]() =А В.
=А В.
Законы операций с константами (пустым и универсальным множествами):
А А; А U А;
А ; А U U;
А А U; АА .
Закон двойного дополнения:
![]() А.
А.
Заметим, что для каждой пары формул, представляющих тот или иной закон, справедливо следующее: одна из формул получается из другой взаимной заменой всех операций пересечения на операции объединения и всех символов на символы U. Этот факт известен под названием принципа двойственности. Заметим также, что для операции пересечения пустое множество имеет свойство нуля, универсальное множество – свойство единицы. Для операции объединения универсальное множество имеет свойство нуля, а пустое множество – свойство единицы.
Формула, в которой присутствуют символы операций над множествами, есть способ задания множества. Две формулы равносильны, если они представляют одно и то же множество. Любую формулу булевой алгебры множеств можно вывести путем равносильных преобразований, используя формулы из приведенного списка. Данный список является достаточным, но для вывода любой формулы данной алгебры можно воспользоваться меньшим списком, т.е. некоторые формулы этого списка можно вывести из других. Например, формулу А В С (А В) (А С) (дистрибутивность объединения относительно пересечения) можно получить следующим образом. Ее правую часть, используя дистрибутивность пересечения, представим как (А В) (А С) (А В) А (А В) С. Раскрыв скобки (по закону ассоциативности), получим (А В) А (А В) С А А В А А С В С. Применим закон идемпотентности и введем константу U (А А А А U), в результате чего после применения закона коммутативности пересечения правая часть примет вид А U А В А С В С. После вынесения за скобки А получим А (U В С) В С, что равно левой части исходного выражения согласно свойству константы U.
Подобным образом выведем закон поглощения А А В А, которого нет в приведенном списке:
А А В А U А В А (U В) А.
Используя принцип двойственности, получим: А (А В) А.
Формулу А В А С А В А С В С выведем следующим образом:
А В А С В С А В А С В С(А А) А В(U С) А С(U В) А В А С.
Используя
только что выведенную формулу и закон
поглощения, докажем А ![]() В А В:
В А В:
А ![]() В А U
В А U ![]() В А U
В А U ![]() В U В А
В U В А ![]() В В А В.
В В А В.
